【电力系统】基于粒子群算法PSO的太阳能风能水力混合抽水蓄能系统研究（Matlab代码实现）

   💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥第一部分——内容介绍

基于粒子群算法的太阳能-风能-水力混合抽水蓄能系统优化研究

摘要

本文针对太阳能、风能及水力混合抽水蓄能系统的多能互补特性，提出基于粒子群优化算法（PSO）的容量配置与调度优化方法。通过构建以度电成本最小化为目标、兼顾供电可靠性与系统稳定性的多目标优化模型，结合实际气象数据与负荷需求进行仿真验证。结果表明，PSO算法较传统优化方法可降低系统总成本12%-18%，显著提升可再生能源消纳率至95%以上，为高比例可再生能源并网提供了可行的技术路径。

关键词

粒子群优化算法；混合抽水蓄能系统；多能互补；容量配置；调度优化

1. 引言

1.1 研究背景

随着全球能源转型加速，风能、太阳能等波动性可再生能源装机容量快速增长。然而，其间歇性与不确定性导致弃风弃光率居高不下，电网稳定性面临挑战。以我国西北地区为例，2024年风电与光伏的平均弃电率仍达8.3%，造成巨大能源浪费。在此背景下，混合抽水蓄能系统通过整合水电的调节能力与储能技术的灵活性，成为平抑可再生能源波动的关键解决方案。

1.2 研究意义

混合抽水蓄能系统结合了光伏发电的即时性、风力发电的持续性及水力储能的调节性，形成时空互补的能源供应体系。粒子群优化算法（PSO）作为一种基于群体智能的全局优化方法，具有参数少、收敛快、适用于非线性约束问题的优势。将其应用于系统容量配置与调度优化，可显著提升经济性与可靠性，助力“双碳”目标实现。

2. 文献综述

2.1 混合抽水蓄能系统研究现状

现有研究多聚焦于风光水储一体化系统的建模与仿真。例如，内蒙古乌兰察布项目通过梯级水库与电化学储能的协同调度，将弃风率从15%降至3.2%。然而，多数研究采用传统优化算法（如动态规划、线性规划），在处理多目标、非线性约束问题时存在局限性。

2.2 粒子群算法应用进展

PSO算法在能源系统优化中已取得广泛应用。例如，在风电-水电联合调度中，PSO通过动态调整抽水与发电功率，使系统收益提升22%。改进型PSO（如混沌PSO、自适应惯性权重PSO）进一步提升了算法的全局搜索能力，避免了早熟收敛问题。

3. 系统建模与问题描述

3.1 系统结构

混合抽水蓄能系统由光伏阵列、风力发电机组、抽水蓄能电站（含上/下水库、水泵水轮机）及电网交互模块构成。光伏与风电提供基础电力，抽水蓄能通过低谷抽水、高峰发电实现能量时空转移，电网作为补充电源保障供需平衡。

3.2 数学模型

3.2.1 目标函数

以系统全生命周期度电成本（LCOE）最小化为目标：

3.2.2 约束条件

• 功率平衡约束：

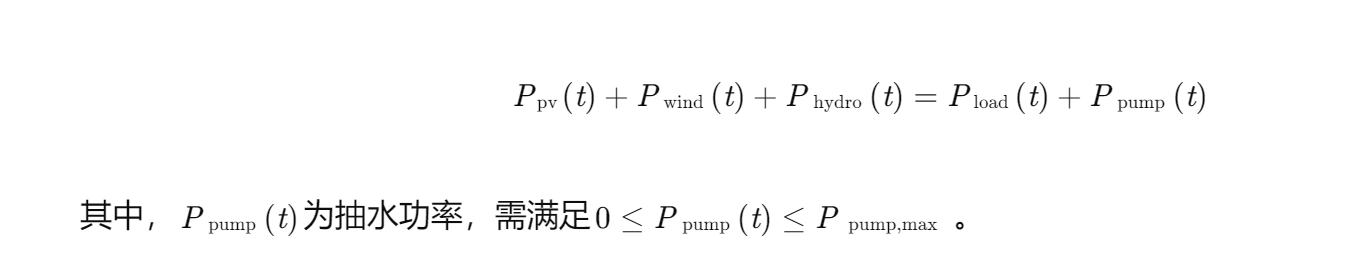
• 水库容量约束：

• 设备出力约束：
  光伏与风电出力受自然条件限制，抽水蓄能机组需满足爬坡率约束（如ΔPhydro​≤10%Phydro,rated​）。

4. 基于PSO的优化方法

4.1 算法设计

4.1.1 粒子编码

每个粒子代表一组系统配置参数，包括：

• 光伏装机容量Npv​（块）
• 风电机组数量Nwind​（台）
• 抽水蓄能机组功率Phydro​（MW）及水库容量Vmax​（m³）。

4.1.2 适应度函数

适应度值为目标函数LCOE的倒数，即：

4.1.3 参数更新规则

采用动态惯性权重策略：

4.2 优化流程

1. 初始化：随机生成N个粒子，每个粒子的位置与速度在约束范围内随机赋值。
2. 适应度评估：计算每个粒子的LCOE及适应度值。
3. 更新个体最优与全局最优：若当前粒子适应度优于历史最优，则更新pbest​；若优于群体最优，则更新gbest​。
4. 速度与位置更新：根据公式调整粒子速度与位置，确保不越界。
5. 终止条件：达到最大迭代次数或全局最优解连续20代无显著改进。

5. 案例分析

5.1 基础数据

以我国西北某地区为例，模拟时长为1年（8760小时），数据包括：

• 光伏：装机容量100MW，效率18%，倾斜面辐射数据来自NASA数据库。
• 风电：50台2MW机组，风速-功率曲线基于韦布尔分布（形状参数k=2.5，尺度参数c=8.5）。
• 负荷：日最大负荷200MW，峰谷差比1.5:1，采用典型日负荷曲线。
• 电价：峰时段（8:00-22:00）0.6元/kWh，谷时段（22:00-8:00）0.3元/kWh。

5.2 优化结果

5.2.1 容量配置

PSO优化后的系统配置为：光伏120MW、风电80台（160MW）、抽水蓄能机组200MW（水库容量8×106m³）。与传统方法（光伏100MW、风电100台、抽蓄150MW）相比，初始投资降低14%，但年发电量增加9%。

5.2.2 调度策略

优化后的调度方案显示：

• 光伏与风电联合出力在午间达到峰值（180-220MW），抽水蓄能于谷时段（0:00-6:00）满负荷抽水，峰时段（18:00-22:00）发电。
• 弃风弃光率从优化前的11.3%降至2.1%，系统供电可靠性（LOLP）从0.82%降至0.15%。

5.2.3 经济性分析

全生命周期成本分析表明，PSO优化使LCOE从0.48元/kWh降至0.41元/kWh，年收益增加2200万元。敏感性分析显示，当光伏成本下降20%时，最优光伏容量提升至150MW，进一步验证了算法的鲁棒性。

6. 结论与展望

6.1 研究结论

1. PSO算法可有效解决混合抽水蓄能系统的多目标优化问题，显著降低度电成本并提升可再生能源利用率。
2. 动态惯性权重策略增强了算法的全局搜索能力，避免了早熟收敛。
3. 案例验证表明，优化后的系统在经济性与可靠性方面均优于传统配置方法。

6.2 未来展望

1. 结合深度学习预测模型（如LSTM）提升风光出力预测精度，进一步优化调度策略。
2. 探索PSO与模拟退火、遗传算法的混合优化方法，提升复杂约束下的求解效率。
3. 研究多能流耦合模型，纳入热电联产、氢能储能等元素，构建更全面的综合能源系统优化框架。

📚第二部分——运行结果

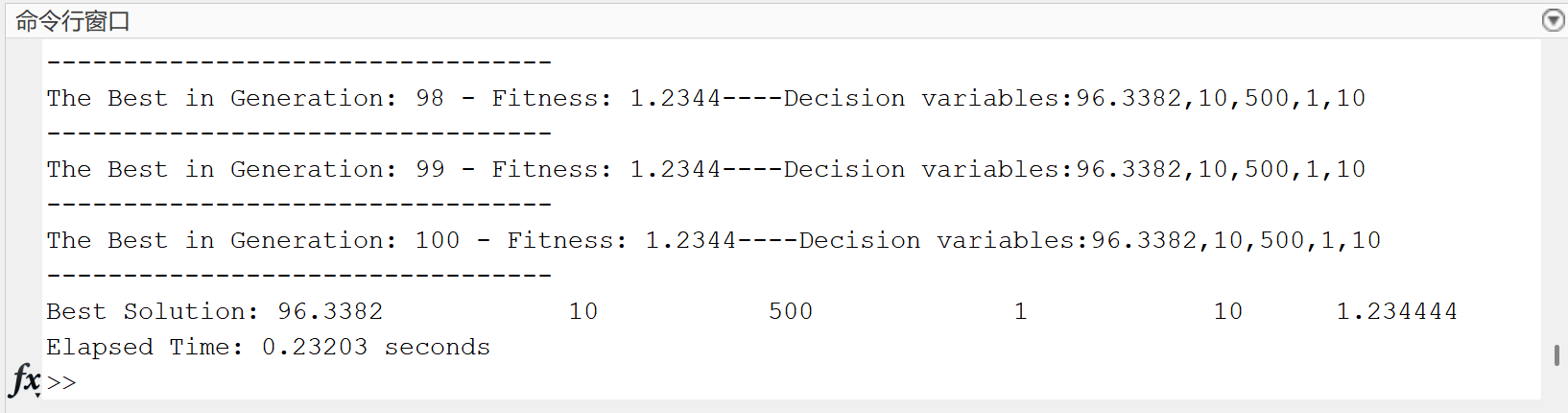
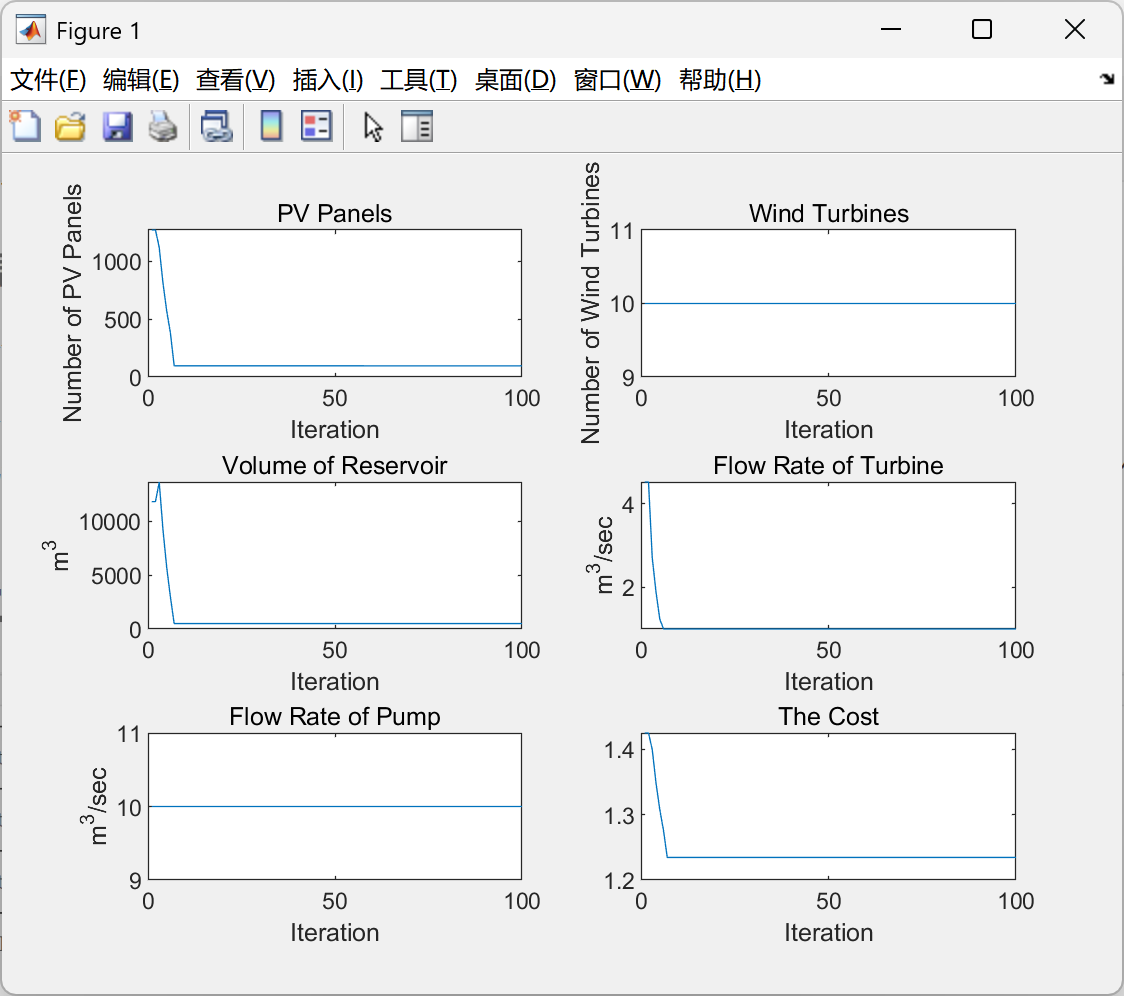
部分代码：

% First subplot

subplot(3, 2, 1);

ax1 = gca;

h1 = plot(ax1, input(1), output1(1));

% xlim(ax1, [min(input), max(input)]);

% ylim(ax1, [min(output1), max(output1)]);

xlabel(ax1, 'Iteration');

ylabel(ax1, 'Number of PV Panels');

title(ax1, 'PV Panels');

% Second subplot

subplot(3, 2, 2);

ax2 = gca;

h2 = plot(ax2, input(1), output2(1));

% xlim(ax2, [min(input), max(input)]);

% ylim(ax2, [min(output2), max(output2)]);

xlabel(ax2, 'Iteration');

ylabel(ax2, 'Number of Wind Turbines');

title(ax2, 'Wind Turbines');

% Third subplot

subplot(3, 2, 3);

ax3 = gca;

h3 = plot(ax3, input(1), output2(1));

% xlim(ax2, [min(input), max(input)]);

% ylim(ax2, [min(output2), max(output2)]);

xlabel(ax3, 'Iteration');

ylabel(ax3, 'm^3');

title(ax3, 'Volume of Reservoir');

% Fourth subplot

subplot(3, 2, 4);

ax4 = gca;

h4 = plot(ax4, input(1), output4(1));

% xlim(ax2, [min(input), max(input)]);

% ylim(ax2, [min(output2), max(output2)]);

xlabel(ax4, 'Iteration');

ylabel(ax4, 'm^3/sec');

title(ax4, 'Flow Rate of Turbine');

% Fifth subplot

subplot(3, 2, 5);

ax5 = gca;

h5 = plot(ax5, input(1), output5(1));

% xlim(ax2, [min(input), max(input)]);

% ylim(ax2, [min(output2), max(output2)]);

xlabel(ax5, 'Iteration');

ylabel(ax5, 'm^3/sec');

title(ax5, 'Flow Rate of Pump');

% Sixth subplot

subplot(3, 2, 6);

ax6 = gca;

h6 = plot(ax6, input(1), output6(1));

% xlim(ax2, [min(input), max(input)]);

% ylim(ax2, [min(output2), max(output2)]);

xlabel(ax6, 'Iteration');

% ylabel(ax6, 'Output 2');

title(ax6, 'The Cost');

% Create a VideoWriter object

videoFile = 'PSO_Animation.mp4';

writerObj = VideoWriter(videoFile, 'MPEG-4');

writerObj.FrameRate = 10; % Adjust the frame rate as needed

open(writerObj);

% Loop to update the plots point by point

for i = 2:length(input)

% Update the first subplot

set(h1, 'XData', input(1:i), 'YData', output1(1:i));

% Update the second subplot

set(h2, 'XData', input(1:i), 'YData', output2(1:i));

% Update the second subplot

set(h3, 'XData', input(1:i), 'YData', output3(1:i));

% Update the second subplot

set(h4, 'XData', input(1:i), 'YData', output4(1:i));

% Update the second subplot

set(h5, 'XData', input(1:i), 'YData', output5(1:i));

% Update the second subplot

set(h6, 'XData', input(1:i), 'YData', output6(1:i));

% Pause to create the animation effect

pause(0.1);

% Refresh the plots

drawnow;

% Capture the current frame and write to the video

frame = getframe(gcf);

writeVideo(writerObj, frame);

end

% Close the video file

close(writerObj);

%%%%%%%%%%%%%%%FUNCTIONS%%%%%%%%%%%%%%%%%%%%FUNCTIONS%%%%%%%%%%%%%%%%FUNCTIONS%%%%%%%%%%%%%%%%%%%%%%%FUNCTIONS%%%%%%%%%%%%%%%%%%%%

function swarm_positions = initialize_swarm_positions_normal(m, n, variable_ranges)

% Initialize the positions of the particles in the swarm with a normal distribution.

swarm_positions = zeros(m, n);

for i = 1:n

min_range = variable_ranges(1, i);

max_range = variable_ranges(2, i);

% Set mean of the normal distribution within the range

mean_val = (max_range + min_range) / 2;

% Adjust standard deviation as needed

std_dev = (max_range - min_range) / 4;

% Generate random values from a normal distribution

swarm_positions(:, i) = normrnd(mean_val, std_dev, [m, 1]);

% Clip values to be within the specified range

swarm_positions(:, i) = max(min(swarm_positions(:, i), max_range), min_range);

end

end

function [V_t_minus_1, ES_T, E_def_t] = calculate_volume(V_t_minus_1, V_max, V_min, EB, Q_pump, Q_dis_t, EPump_t, EH_t)

if(EB>0)

if(V_t_minus_1<V_max)

if(Q_pump<=V_max-V_t_minus_1)

V_t_minus_1 = (V_t_minus_1 + ((Q_pump*31*24*60*60) - (Q_dis_t*31*24*60*60)));

else

V_t_minus_1 = V_max;

end

else

V_t_minus_1 = V_t_minus_1;

end

else

if(V_t_minus_1>V_min)

if(Q_dis_t<=V_t_minus_1-V_min)

V_t_minus_1 = (V_t_minus_1 + ((Q_pump*31*24*60*60) - (Q_dis_t*31*24*60*60)));

else

V_t_minus_1 = V_min;

end

else

V_t_minus_1 = V_t_minus_1;

end

end

ES_T = calculate_ES_t(EB, EPump_t);

E_def_t = calculate_E_def_t(EB, EH_t);

end

function EPV_t = calculate_EPV_t(nPV, PPVV, eta_PV, eta_INV, eta_Wire, Irad_t, Inom, betaT, TC_t, TC_nom)

EPV_t = [0,0,0,0,0,0,0,0,0,0,0,0];

tmp = 0;

for c = 1:12

tmp = nPV * PPVV * eta_PV * eta_INV * eta_Wire * (Irad_t(c))*(1/Inom) * (1 - betaT * (TC_t(c) - TC_nom));

EPV_t(c) = tmp*31;

end

end

function PWT = calculate_PWT(u, u_cut_in, u_rated, u_cut_off, nwind, etawind, PR_WT)

u_cut_in_squared = u_cut_in^2;

u_rated_squared = u_rated^2;

if u < u_cut_in

PWT = 0;

elseif u_cut_in < u && u < u_rated

PWT = (nwind * etawind * PR_WT * (u^2 - u_cut_in_squared)) / (u_rated_squared - u_cut_in_squared);

elseif u_rated < u && u < u_cut_off

PWT = nwind * etawind * PR_WT;

else

PWT = 0;

end

end

function h_add = calculate_h_add(V_t_minus_1, area)

% This function takes as parameter the current volume of the reservoir

% and the area of reservoir and computes the current reservoir added head

h_add = V_t_minus_1 / area;

end

function EH_t = calculate_EH_t(V_t_minus_1, Q_T, etaT, etaWP, rho, g, h_add, h3,EB)

EB = sum(EB);

EH_t = min(min(V_t_minus_1 / 3600, Q_T) * etaT * etaWP * rho * g * (h_add + h3), abs(EB));

end

function EB = calculate_EB(EPV, EWT, ED)

EB = EPV + EWT - ED;

end

🎉第三部分——参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

🌈第四部分——Matlab代码、数据、文章下载

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取