【吴恩达机器学习】监督学习：回归与分类

InquisiG

已于 2025-02-11 14:32:16 修改

阅读量1.3k

点赞数 40

分类专栏：吴恩达机器学习文章标签：机器学习 python 回归分类数据分析

于 2025-02-10 16:18:20 首次发布

本文链接：https://blog.csdn.net/2301_77253539/article/details/145521885

版权

1 机器学习

监督学习与无监督学习

（一）监督学习（Supervised learning）

（二）无监督学习（Unsupervised learning）

梯度下降的一种替代方法——正规方程（Normal Equation）

3.4 特征缩放

3.4.1 除以最大值

3.4.2 均值归一化（Mean normalization）

3.4.3 Z-分数归一化（Z - score normalization）

4 逻辑回归（logistic regression）

高方差（High Variance）——过拟合

4.5 解决过拟合

4.5.1 收集更多的训练数据

4.5.2 减少特征，进行“特征选择”

4.5.3 正则化（Regularization）

1 机器学习

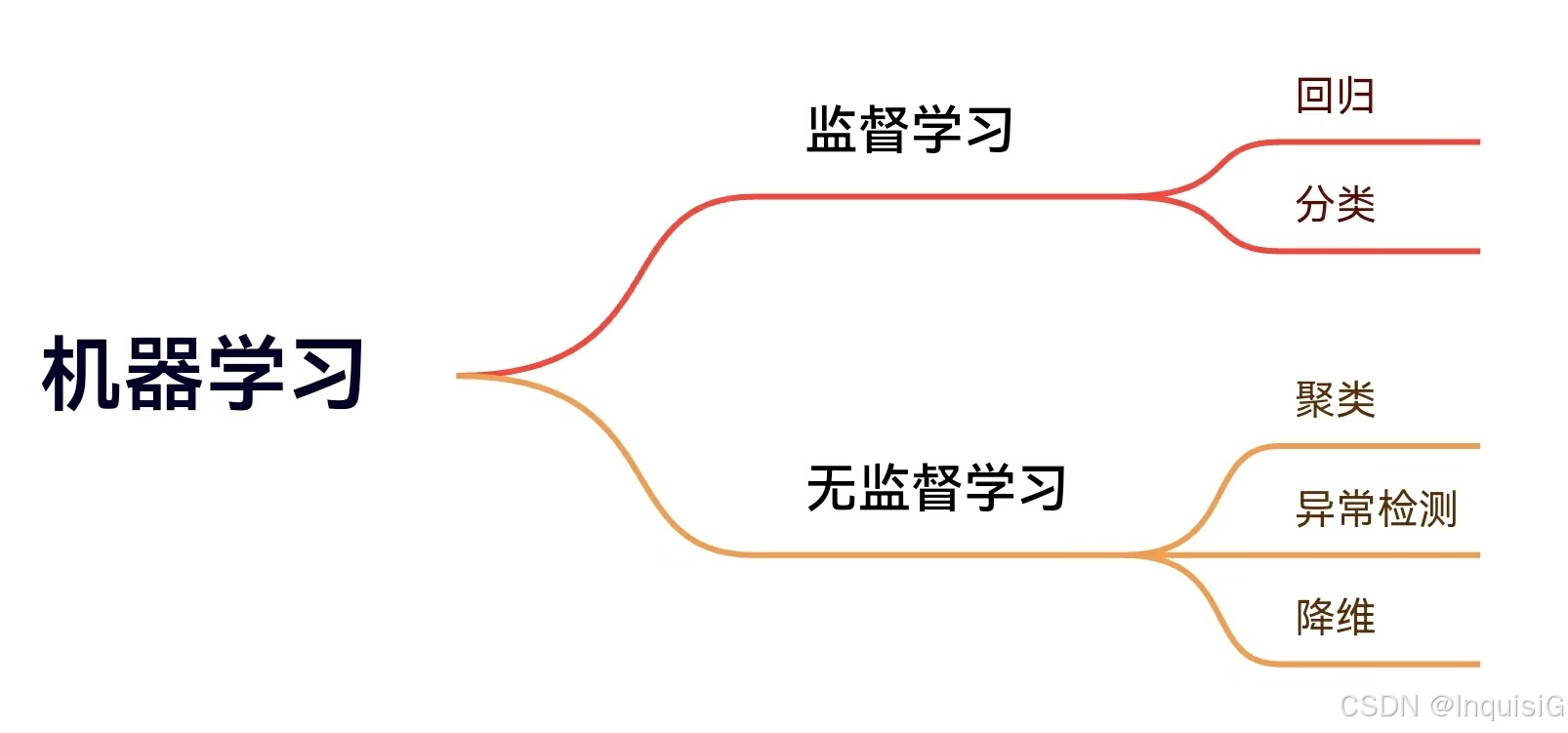
监督学习与无监督学习

（一）监督学习（Supervised learning）

监督学习是在已知正确答案（标签）的数据集上进行训练的学习方式。其主要任务分为回归和分类。

回归：预测连续型数值。例如，根据房屋的各种特征（面积、房间数量等）预测房价，这里房价是一个连续的数值。

分类：预测离散型类别。比如，根据肿瘤的大小判断其是良性还是恶性，结果只有 “良性” 和 “恶性” 两种类别。

（二）无监督学习（Unsupervised learning）

无监督学习是在没有预先标注标签的数据集上进行学习。它旨在发现数据中的内在结构和模式。无监督学习不需要预先知道数据的类别，能够帮助我们从复杂的数据中挖掘出有价值的信息。

聚类：将相似的数据点归为一组，实现对数据的分类整理。在新闻领域，可把主题相同的新闻文章归在一起；在客户数据分析中，依据客户的特征和行为，划分不同的市场细分群体。

降维：用较少的数据表示原有数据，降低数据维度，去除冗余信息，在不损失关键信息的前提下简化数据，提升处理效率。

异常检测：找出数据集中与其他数据差异较大、不符合常规模式的异常点。在网络安全监测、设备故障检测等方面有重要应用，及时发现异常情况，保障系统正常运行。

2 一元线性回归（单变量线性回归）

2.1 线性回归模型

2.1.1 认识数据集

2.1.2 公式

$f_{w, b}(x) = wx + b$

通过训练数据集来调整 $w$ 和 $b$ 的值，使得模型能够尽可能准确地预测目标值。

2.2 成本函数（代价函数）

2.2.1 公式

成本函数衡量模型预测值与真实值的差距，目标是找到使成本最小的 w 和 b。

一个变量的成本方程式是：

$J(w, b) = \frac{1}{2m} \sum_{i=0}^{m-1} \left( f_{w, b}(x^{(i)}) - y^{(i)} \right)^2$

m是数据集中的训练实例的数量

计算成本的函数如下：

def compute_cost(x, y, w, b): 
    """
    Computes the cost function for linear regression.
    
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    
    Returns
        total_cost (float): The cost of using w,b as the parameters for linear regression
               to fit the data points in x and y
    """
    # number of training examples
    m = x.shape[0]    #通过x数组的形状获取训练样本的数量m
    
    cost_sum = 0 
    for i in range(m): 
        f_wb = w * x[i] + b   
        cost = (f_wb - y[i]) ** 2  
        cost_sum = cost_sum + cost  
    total_cost = (1 / (2 * m)) * cost_sum  

    return total_cost

2.2.2 直观理解

2.3 梯度下降

2.3.1 原理

梯度下降通过迭代更新参数，逐步逼近成本函数的最小值：

$w = w - \alpha \frac{\partial J(w, b)}{\partial w}$

$b = b - \alpha \frac{\partial J(w, b)}{\partial b}$

2.3.2 直观理解

2.3.3 学习率

2.3.4 线性回归的梯度下降

梯度的定义为：

$\frac{\partial J(w, b)}{\partial w} = \frac{1}{m} \sum_{i=0}^{m-1} (f_{w, b}(x^{(i)}) - y^{(i)}) x^{(i)}$

$\frac{\partial J(w, b)}{\partial b} = \frac{1}{m} \sum_{i=0}^{m-1} (f_{w, b}(x^{(i)}) - y^{(i)})$

计算梯度公式：

def compute_gradient(x, y, w, b): 
    """
    Computes the gradient for linear regression 
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    Returns
      dj_dw (scalar): The gradient of the cost w.r.t. the parameters w
      dj_db (scalar): The gradient of the cost w.r.t. the parameter b     
     """
    
    # Number of training examples
    m = x.shape[0]    
    dj_dw = 0
    dj_db = 0
    
    for i in range(m):  
        f_wb = w * x[i] + b 
        dj_dw_i = (f_wb - y[i]) * x[i] 
        dj_db_i = f_wb - y[i] 
        dj_db += dj_db_i
        dj_dw += dj_dw_i 
    dj_dw = dj_dw / m 
    dj_db = dj_db / m 
        
    return dj_dw, dj_db