电磁场与电磁波 实验四 有限差分法处理电磁场问题

一、实验名称：

实验四 有限差分法处理电磁场问题

二、实验目的：

有限差分法绘制带电长圆柱体的电位和电力线图像。

三、实验原理及步骤:

1.基本原理

在很多实际情况下，往往我们不知道电荷的分布情况，而只知道边界的电位。

例如在静电场中的导体，边界是等位面，但是表面上的电荷分布往往不一样，而且很难求得。

如果我们想求导体附近的电场，可以使用用差分法解电场的方法。

解决这个问题的关键是对电位使用以下结论：在一个没有电荷的区域，给出一个点的电位等于周围点的电位数值的平均值。使用高斯定律以及以下公式来证明这个结论：

（根据电压V的电场分量）

将集中讨论该情况，其中电位只取决于两个坐标，x和y。一个例子是一个带电的长圆柱体。在一个点的电势只依赖于这一点在平面垂直于圆柱体的轴线，而不是z坐标。对于这样一个二维的情况下，考虑一个点P的坐标（x，Y，Z），并在一个由高斯表面封闭的立方体的一面长度是2Δl，中心在P（图）。如果立方体的内部没有电荷，通过立方体的电通量ΦE等于零。由方程  可知Z轴的电场分量为零，因为电势V并不是z的函数。因此，并没有通过高斯表面的平行于xy -平面的电通量。由于是一个小的立方体，通过其他四个面每通量有一个良好的逼近，等于在每面的中心和每一面的（2Δl）2的E的垂直分量的乘积 。总流量（等于0）可以表示为；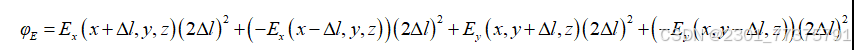

在一个没有电荷的区域，点P的电位数值等于P点周围电位值的平均值。

图4  没有电荷的区域，点P的电位的求解示意图

使用式，可以近似的写出电场的各分量：

（）

可以得到P点的位是：

总之，P点的电位值等于P点周围点的电位值的平均值，前提是l非常小。

2.计算机绘图算法

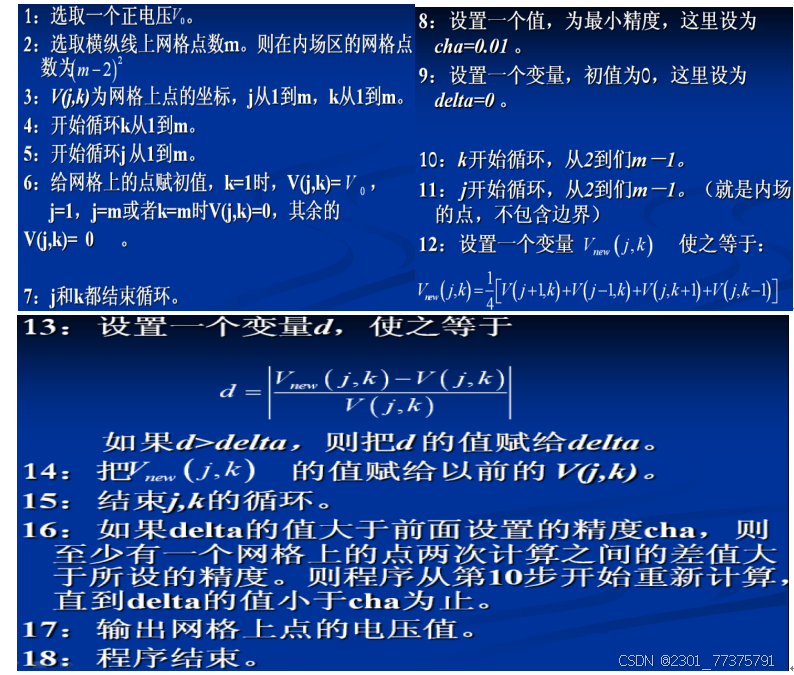
3.参考程序

计算场点电压值程序如下：

m=12

for k=1:m

    for j=1:m

        if k==1

            V(j,k)=1;

        elseif((j==1)|(j==m)|(k==m))

                V(j,k)=0;

            else

                V(j,k)=1;

            end

    end

end

cha=0.01;delta=0;

n=0;

while(1)

    n=n+1;

   for k=2:m-1

    for j=2:m-1

        Vnew(j,k)=1/4*(V(j+1,k)+V(j-1,k)+V(j,k+1)+V(j,k-1));

        d=abs((Vnew(j,k)-V(j,k))/V(j,k));

        if d>delta

            delta=d;

        end

     V(j,k)=Vnew(j,k);  

end

  end

  if delta<cha

      break;

  end

  if(n>100)

      break;

  end

  delta=0.;

end

代入m＝22

绘图程序：

k=1:m;j=1:m;

[DX,DY] = gradient(V,.4,.4);

hold on

quiver(k,j,DX,DY,2)

hold off

k=1:m;

j=1:m;

[DX,DY]=gradient(V,.4,.4)

A=(DX.^2+DY.^2).^0.3;

[DA,DB]=gradient(A,.4,.4);

hold on

quiver(k,j,DA,DB,2)

hold off

3.程序参考运行结果

电场图和电力线图分别如图、图所示。

图1 电场线的图像                      图2 电力线的图像

四、实验时间

2024年12月9日

五、实验仪器：

1、计算机               1台

2、MATLAB 仿真软件    1套

六、实验结果：

代码

m=22
for k=1:m
    for j=1:m
        if k==1
            V(j,k)=1;
        elseif((j==1)|(j==m)|(k==m))
                V(j,k)=0;
            else
                V(j,k)=1;
            end
    end
end
cha=0.01;
delta=0;
n=0;
while(1)
    n=n+1;
   for k=2:m-1
    for j=2:m-1
        Vnew(j,k)=1/4*(V(j+1,k)+V(j-1,k)+V(j,k+1)+V(j,k-1));
        d=abs((Vnew(j,k)-V(j,k))/V(j,k));
        if d>delta
            delta=d;
        end
     V(j,k)=Vnew(j,k);  
end
  end
  if delta<cha
      break;
  end
  if(n>100) 
      break;
  end
  delta=0.;
end
k=1:m;
j=1:m;
[DX,DY] = gradient(V,.4,.4);
hold on
quiver(k,j,DX,DY,2)
hold off
k=1:m;
j=1:m;
[DX,DY]=gradient(V,.4,.4)
figure(1)
A=(DX.^2+DY.^2).^0.3;
[DA,DB]=gradient(A,.4,.4);
figure(2)
hold on
quiver(k,j,DA,DB,2)
hold off

                                     图3 电场线的图像                      图4 电力线的图像