CS224W图神经网络的表达能力有多强？（How Expressive are Graph Neural Networks）

magic-hl

已于 2024-03-24 22:51:36 修改

阅读量102

点赞数

文章标签：人工智能深度学习

于 2023-08-18 10:09:58 首次发布

本文链接：https://blog.csdn.net/2301_79012932/article/details/132354047

版权

GNN 有多强大？
        已经提出了许多 GNN 模型（例如 GCN、GAT、GraphSAGE、design space）。
        这些GNN模型的表达能力（区分不同图结构的能力）是多少？
        如何设计一个最具表达力的GNN模型？

在这个图中，我们要去比较（1，5），（1，4），（1，2）

关键问题：GNN 节点嵌入能否区分不同节点的局部邻域结构？
        ▪ 如果是，什么时候？如果不是，GNN 什么时候会失败？
接下来：我们需要了解 GNN 如何捕获局部邻域结构。
        ▪ 关键概念：计算图

计算图：

在每一层中，GNN 都会聚合相邻节点的嵌入。
GNN 通过邻域定义的计算图生成节点嵌入。
        如何去理解（1，2）是一样的点呢？因为他们的计算图是一样的，把标签直接拿掉就好比较了。

GNN 将为节点 1 和 2 生成相同的嵌入，因为：
        ▪ 计算图是相同的。
        ▪ 节点特征（颜色）相同。

一般来说，不同的局部邻域定义不同的计算图

计算图与每个节点周围的有根子树结构相同。

GNN 的节点嵌入捕获有根子树结构。
最具表现力的 GNN 将不同的根子树映射到不同的节点嵌入（用不同的颜色表示）。

单射函数：

函数 𝑓:𝑋 → Y 如果将不同的元素映射到不同的输出，则为单射（injective）。
直观理解：𝑓 保留有关输入的所有信息。

GNN的表达能力怎么样？

最具表达力的图神经网络应该将子树单射地映射到节点嵌入中。

关键观察：相同深度的子树可以从叶节点递归地特征化，直到根节点。

如果图神经网络（GNN）的每个聚合步骤都能够完全保留邻居信息，生成的节点嵌入可以区分不同的以不同节点为根的子树。

换句话说，最具表达力的图神经网络在每一步都会使用一个单射的邻居聚合函数。
        ▪ 将不同的邻居映射到不同的嵌入中。

1. 设计最强大的图神经网络（Designing the Most Powerful Graph Neural Network）

关键观察：GNN 的表达能力可以通过它们使用的邻居聚合函数来表征。
▪ 更具表现力的聚合函数会导致 GNN 更具表现力。
▪ 单射聚合函数产生最具表现力的GNN。

下一步：
▪ 从理论上分析聚合函数的表达能力

观察：邻居聚合可以抽象为多集（具有重复元素的集合）上的函数。
下一步：我们分析两种流行的GNN模型的聚合函数
▪ GCN（均值池）[Kipf & Welling, ICLR 2017] ▪ 对相邻节点特征使用逐元素均值池
▪ GraphSAGE（最大池）[Hamilton 等人。 NeurIPS 2017] ▪ 在相邻节点特征上使用元素最大池化

1.1 GCN（平均池）[Kipf & Welling ICLR 2017]

        ▪ 取元素均值，然后是线性函数和 ReLU 激活，即 max(0, 𝑥)。
        ▪ 定理[Xu 等人。 ICLR 2019]
        ▪ GCN 的聚合函数无法区分具有相同颜色比例的不同多重集。

   为了简单起见，我们假设节点特征（颜色）由 one-hot 编码表示。
▪ 示例：如果有两种不同的颜色：

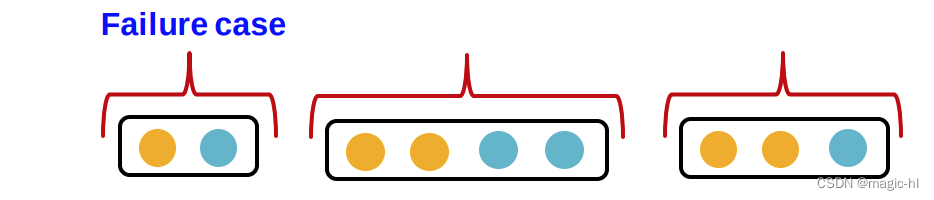
▪ 这个假设足以说明GCN 是如何失败的。

           ▪失败案例图解

1.2 GraphSAGE（最大池）[Hamilton 等人。神经IPS 2017]

        ▪ 应用MLP，然后逐元素取最大值。
        ▪ 定理[Xu 等人。 ICLR 2019]
        ▪ GraphSAGE 的聚合函数无法区分具有同一组不同颜色的不同多组。

        ▪失败案例图解

总结：我们分析了 GNN 的表达能力。
主要要点：
        ▪ GNN 的表达能力可以通过邻居聚合函数的表达能力来表征。
        ▪ 邻居聚合是多集（具有重复元素的集）上的函数
        ▪ GCN和GraphSAGE的聚合函数无法区分一些基本的多重集；因此不是单射的。
        ▪ 因此，GCN 和 GraphSAGE 并不是最强大的 GNN。

我们的目标：在消息传递 GNN 类中设计最强大的 GNN。
这可以通过设计多重集上的单射邻居聚合函数来实现。
在这里，我们设计了一个可以对单射多重集函数进行建模的神经网络。

定理
任何单射多集函数都可以表示为：

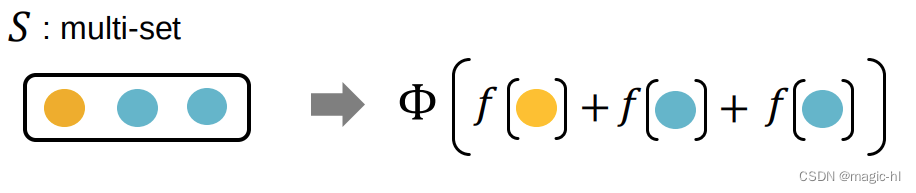
证明直觉：
𝑓 产生颜色的独热编码。 one-hot 编码的求和保留了有关输入多重集的所有信息。

如何在 $\phi \left ( \sum_{x\in s}f\left ( x \right )\right )$ 中建模 𝜱 和 𝒇 ？
我们使用多层感知器（MLP）。
定理：通用逼近定理
▪ 具有足够大隐藏维度和适当非线性 𝜎(⋅)（包括 ReLU 和 sigmoid）的 1 隐藏层 MLP（包括 ReLU 和 sigmoid）可以将任何连续函数逼近为任意值准确性.

▪ 我们已经得到了一个可以对任何单射多重集函数进行建模的神经网络。

$MLP_{\phi }\left ( \sum_{x\in S}MLP_{f}\left ( x \right )\right )$

▪ 实际上，MLP 隐藏维数为 100 到 500 就足够了。

图同构网络（GIN）
        ▪ 应用 MLP、逐元素求和，然后应用另一个 MLP。
                                                 $MLP_{\phi }\left ( \sum_{x\in S}MLP_{f}\left ( x \right )\right )$
定理
        ▪ GIN 的邻居聚合函数是单射的。
▪ 无失败案例！
▪ GIN 是我们介绍的消息传递 GNN 类中最具表现力的 GNN！
▪ 到目前为止：我们已经描述了GIN 的邻居聚合部分。
▪ 我们现在通过将GIN 与WL 图内核（获取图级特征的传统方法）联系起来来描述GIN 的完整模型。
        ▪ 我们将看到GIN 如何成为WL 图内核的“神经网络”版本。
回想一下：WL 内核中的颜色细化算法。
        给定：带有一组节点 𝑉 的图 𝐺。
                ▪ 为每个节点𝑣 分配初始颜色 $c^{\left ( 0 \right )}\left ( v \right )$ 。
                ▪ 通过 $c^{\left ( k + 1 \right )}\left ( v \right ) = HASH\left (c^{\left ( k \right )}\left ( v \right ), c^{\left ( k \right )}\left ( u\right )_{u\in N\left ( \nu \right )}\right )$ 迭代细化节点颜色，其中 HASH 将不同的输入映射到不同的颜色。
               ▪ 经过𝐾 步颜色细化后， $c^{\left ( k \right )}\left ( v \right )$ 总结了𝐾-hop 邻域的结构

元组上的任何单射函数

$c^{\left ( k + 1 \right )}\left ( v \right ) = HASH\left (c^{\left ( k \right )}\left ( v \right ), c^{\left ( k \right )}\left ( u\right )_{u\in N\left ( \nu \right )}\right )$

都可以建模成

$MLP_{\phi }\left ( \left ( 1 +\varepsilon \right )\cdot MLP_{f} \left ( c^{\left ( k \right )}\left ( v \right )\right ) + \sum_{u\in N\left ( \nu \right )}MLP_{f} \left ( c^{\left ( k \right )}\left ( u \right )\right ) \right )$

GIN 的节点嵌入更新

给定：具有一组节点 𝑉 的图 𝐺。

▪ 为每个节点𝑣 分配一个初始向量 $c^{\left ( 0 \right )}\left ( v \right )$ 。

▪ 通过 $c^{\left ( k + 1 \right )}\left ( v \right ) = GINConv\left (c^{\left ( k \right )}\left ( v \right ), c^{\left ( k \right )}\left ( u\right )_{u\in N\left ( \nu \right )}\right )$ 迭代更新节点向量，其中 GINConv 将不同的输入映射到不同的嵌入。

▪ 经过GIN 迭代K步骤后， $c^{\left ( k \right )}\left ( v \right )$ 总结了𝐾-hop 邻域的结构。

GIN 相对于 WL 图内核的优点是：
        ▪ 节点嵌入是低维的；因此，它们可以捕获不同节点的细粒度相似性。
        ▪ 可以为下游任务学习更新函数的参数。
由于GIN和WL图内核之间的关系，它们的表达是完全相同的。
        ▪ 如果两个图可以通过GIN 来区分，那么它们也可以通过WL 内核来区分，反之亦然。
这有多强大？
        ▪ WL 核在理论上和经验上都被证明可以区分大多数现实世界的图。
        ▪ 因此，GIN 也足够强大，可以区分大多数真实的图！

均值池和最大池的失败案例：

按判别力排名：

是否可以提升图神经网络的表达能力？
        ▪ 存在基本的图结构，现有的图神经网络框架无法区分，比如循环中的差异。
        ▪ 可以通过提升图神经网络的表达能力来解决上述问题。[You等人，AAAI 2021；Li等人，NeurIPS 2020]
                ▪ 敬请关注第15讲：图神经网络中的高级主题。

总结：
        我们设计了一个可以对单射多集函数进行建模的神经网络。
        我们使用神经网络进行邻居聚合函数，得到了 GIN——最具表现力的 GNN 模型。
        关键是使用逐元素求和池化，而不是均值/最大池化。
        GIN 与 WL 图内核密切相关。
        GIN 和 WL 图内核都可以区分大部分真实图！

2. 当事情不按计划进行时（When Things Don't Go As Planned）

数据预处理很重要：
        ▪ 节点属性可能有很大差异！使用标准化
        ▪ 例如概率范围 (0,1)，但某些输入可能具有更大的范围，例如 (−1000, 1000)
优化器：ADAM 对学习率相对稳健
激活函数
        ▪ ReLU 激活函数通常效果很好
        ▪ 其他好的替代方案：LeakyReLU、PReLU
        ▪ 输出层没有激活函数
        ▪ 每层都包含偏置项
嵌入尺寸：
        ▪ 32、64 和 128 通常是很好的起点

调试问题：训练期间损失/准确性不收敛
        ▪ 检查管道（例如，在 PyTorch 中我们需要 Zero_grad）
        ▪ 调整学习率等超参数
        ▪ 注意权重参数初始化
        ▪ 仔细检查损失函数！
对于模型开发很重要：
        ▪ 对（部分）训练数据的过度拟合：
        ▪ 对于小的训练数据集，损失应该基本上接近于 0，并且具有表达性的神经网络
        ▪ 监控训练和验证损失曲线