数学建模(2)Topsis模型/优劣解距离法

潮汐退涨月冷风霜

已于 2024-02-15 11:59:00 修改

阅读量257

点赞数 3

文章标签：数学建模

于 2024-02-15 11:50:49 首次发布

本文链接：https://blog.csdn.net/2301_79376014/article/details/136119283

版权

该篇文章介绍了如何在Matlab中运用正向化技术（包括极小型、中间型和区间型转换）对评价矩阵进行处理，然后通过标准化和计算得分来解决有数据的评价类问题。文章还提及了如何使用熵权法确定指标间的权重。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

应用于有数据的评价类问题

Step 1：将原始矩阵正向化

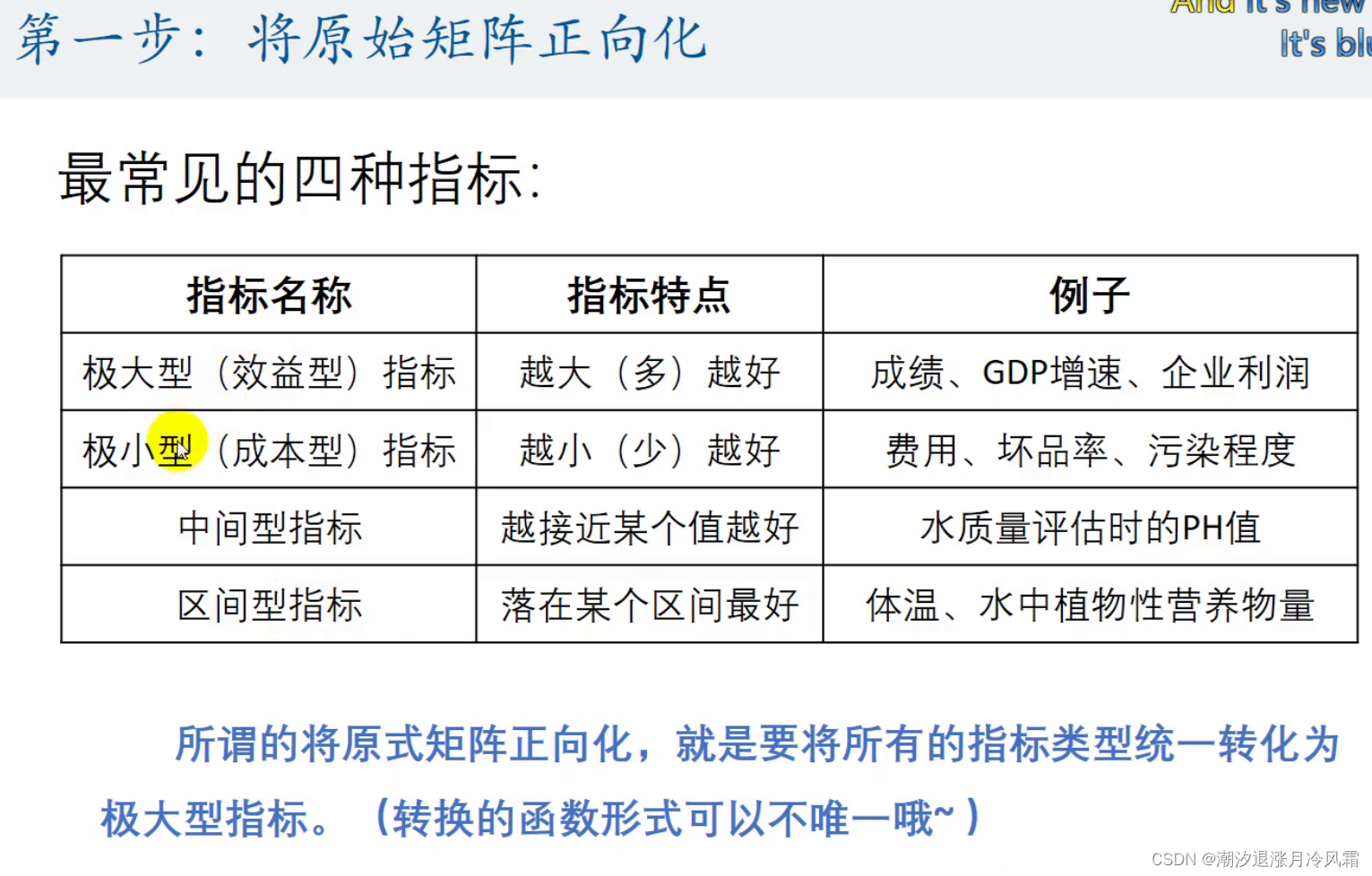
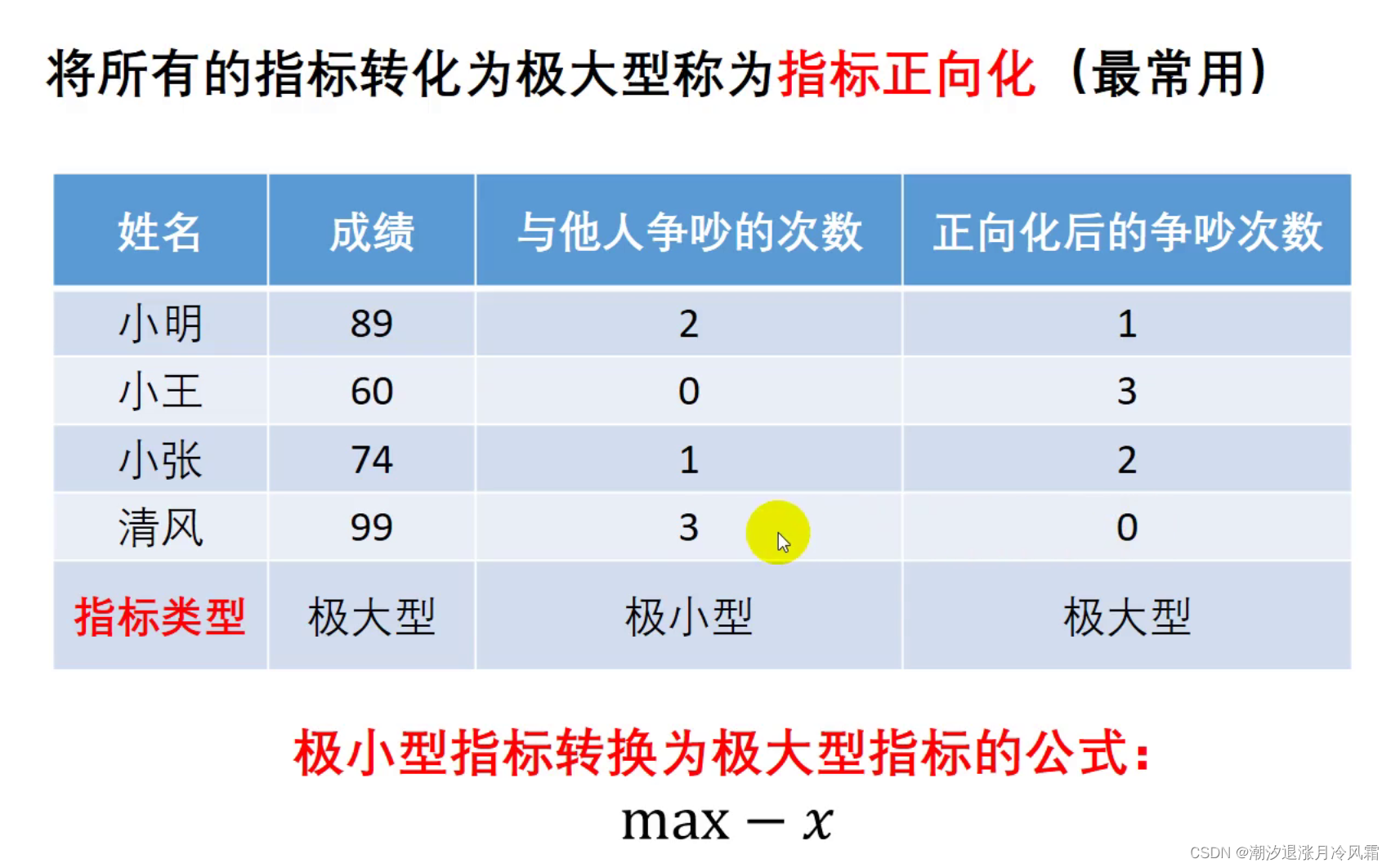
极小型转极大型

中间型转极大型

区间型转极大型

Step 2: 正向矩阵标准化

Step 3: 计算得分并归一化

注释：这里可以确定各指标间的权重wj，可以使用上一节学习的判断矩阵也可以使用后面讲的熵权法

Matlab参考实现代码

主文件

Topsis.m
%第一步 将原始矩阵正向化
[n,m]=size(X);
disp(['共有' num2str(n) '个评价对象,' num2str(m) '个评价指标！'])
Judge=input(['这' num2str(m) '个评价指标是否需要正向化处理，需要输入1，不需要输入0:']);
if(Judge==1)
Position=input('请输入需要正向化的指标所在列，例如第1、2、4三列需要处理，输入[1,2,4]:');
disp('请输入需要正向化处理的这些列的指标类型(1:极小型,2:中间型,3:区间型):');
Type=input('例如第1列是中间型，第2列是区间型，第3列是极小型，输入[2,3,1]:');
for i=1:size(Position,2)
  X(:,Position(i))=Positivization(X(:,Position(i)),Position(i),Type(i));
end
end
disp('正向化后矩阵为:')
disp(X);
%第二步：将正向化矩阵标准化
Z=X./repmat(sum(X.^2,1).^0.5,n,1);
disp("标准化矩阵 Z=")
disp(Z)

%第三步：计算与最大值、最小值之间的距离
%max(M) M每一列最大值构成的向量
%max(M:) M中最大元素
D_P=sum([(Z-repmat(max(Z),n,1)).^2],2).^0.5;%D+与最大值的距离向量
D_N=sum([(Z-repmat(min(Z),n,1)).^2],2).^0.5;%D-与最小值的距离向量
S=D_N./(D_P+D_N);  
disp('最后的得分是:');
Last_S=S/sum(S) //归一化
[sorted_S,index]=sort(Last_S,'descend')
%向量默认升序排列，需降序加‘descend’
%矩阵sort(A) 对每一列升序排列
%sort(A,2)对每一行升序排列 [sA,index] sA是排序好的向量，index是sA在A中的索引

正向化函数文件

Min2Max.m
function [posit_X]=Min2Max(X)
%数字和矩阵做运算（和每个元素做运算）
posit_X=max(X)-X;
end

Mid2Max.m
function [posit_X]=Mid2Max(X,mid)
%abs 可以对矩阵所有元素取绝对值
M=max(abs(X-mid));
posit_X=1-abs(X-mid)/M;
end

In2Max.m
function [posit_X]=In2Max(X,low,high)
M=max([low-min(X),max(X)-high]);
for i=1:size(X)
  if X(i)>=low&&X(i)<=high
    X(i)=1;
  elseif X(i)<low
    X(i)=1-(low-X(i))/M;
  elseif X(i)>high
    X(i)=1-(X(i)-high)/M;
  end
end
  posit_X=X;
end

Positivization.m

function[posit_X]=Positivization(X,i,type) %矩阵 列号 类型

if type==1
disp(['第' num2str(i) '列是极小型,正在正向化:']);
posit_X=Min2Max(X);
disp(['第' num2str(i) '列极小型正向化处理完成:'])
disp('~~~~~~~~~~~~~~~~~~~~~~分割线~~~~~~~~~~~~~~~~~~~~~~~');
elseif type==2
disp(['第' num2str(i) '列是中间型,正在正向化:']);
mid=input('输入最佳值:');
posit_X=Mid2Max(X,mid);
disp(['第' num2str(i) '列中间型正向化处理完成:'])
disp('~~~~~~~~~~~~~~~~~~~~~~分割线~~~~~~~~~~~~~~~~~~~~~~~');
elseif type==3
disp(['第' num2str(i) '列是区间型,正在正向化:']);
low=input('输入最佳区间下界');
high=input('输入最佳区间上界');
posit_X=In2Max(X,low,high);
disp(['第' num2str(i) '列区间型正向化处理完成:'])
disp('~~~~~~~~~~~~~~~~~~~~~~分割线~~~~~~~~~~~~~~~~~~~~~~~');
end
end

补充：熵权法确定权重

信息量和信息熵

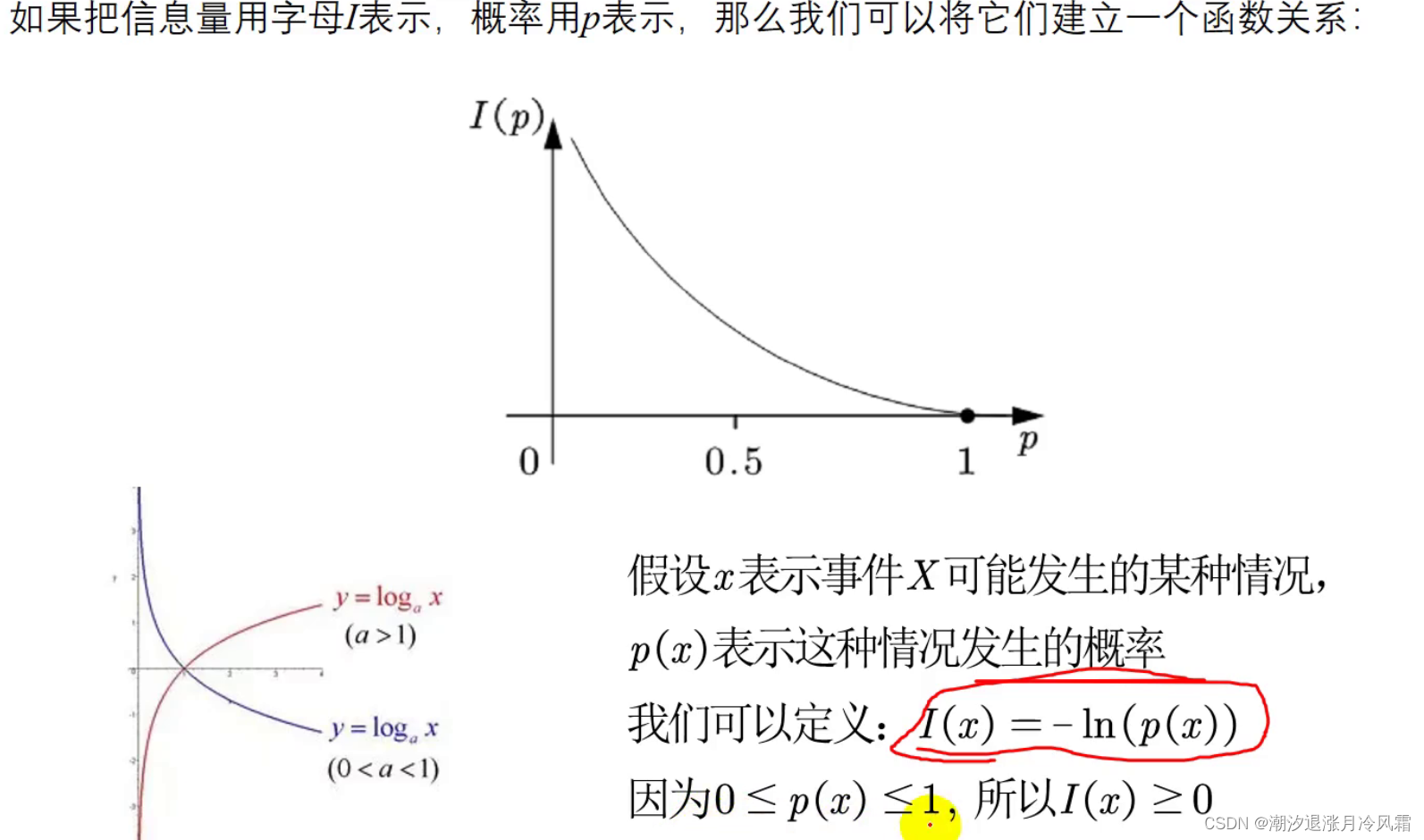
熵权法步骤

Matlab参考代码实现

function  [W]=Entroy_Method(Z)
% 计算有n个样本，m个指标的样本所对应的熵权
%输入：Z：n*m的矩阵（经过正向化和标准化，且元素中不存在负数）
%输出：熵权，m*1的列向量
[n,m]=size(Z);
%一个指标一个指标计算信息效能值
D=zeros(m,1);
for i=1:m
    X=Z(:,i);
    p=X/sum(X);
    e=-sum(mylog(p).*p)/log(n);
    D(i)=1-e;
end
W=D/sum(D);
end

function [logp]=mylog(p)
n=length(p);
logp=zeros(n,1);
for i=1:n
    if p(i)==0
        logp(i)=0;
    else
        logp(i)=log(p(i));
    end    
end
end