傅里叶变换为什么必须满足函数绝对可积

本文用作学习信号与系统知识

首先，要知道傅里叶变换是一种将信号从时间域转换到频率域的一个工具，其将一个函数表示为频率成分的线性组合。

为什么傅里叶变换的存在条件之一是该函数必须保证绝对可积呢？

因为这个条件可以确保傅里叶变换的收敛性----也就是说其变换后的频率成分可以被很好的表示和计算

首先我们要明白  什么是函数的绝对可积性：（函数的绝对值的积分是有限的）

一个函数f(x) 被称为绝对可积，是指其在定义域上的绝对值的积分是有限的。简单来说：就是一个函数的“面积”不能够太大。具体一点就是：如果你把这个函数在整个定义域（一般是负无穷到正无穷）上面做“面积计算”，那么这个面积就是要有限的，也就是说是一个可以被算出具体数值的数，而不是无穷大。公式如下：

                                                

这个可以保证傅里叶变换可以通过积分得到一个确定的结果。
这个公式的意思：我们把f（x）的绝对值取出来，然后从x=−∞ 到 x=+∞ 对它进行积分结果必须是一个有限的数。如果是无穷大的话，就说明函数不是绝对可积的。

举俩个例子吧：

例子1：快速衰减的函数

                                                 
算一下：结果是2  所以他绝对可积

例子2：不衰减的函数
                                                

这个虽然在俩个无穷处趋向为0，但是他衰减的很慢，所以他的面积下不来。

算出来的结果也就是无穷大（发散），所以其不是绝对可积的

所以我们现在就已经明确了什么是函数的绝对可积性

----------------------------------------------分割线--------------------------------------------------------

下面说明为什么傅里叶变换需要这个条件呢：

傅里叶变换的定义涉及到对f（x）和复指数函数e^−iωx 的乘积进行积分

                                        
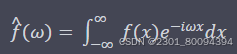
注意：大学里一般我们复数使用 j ，因为电流中的 i 表示电流 ，为了避免误解 。但是此处我使用的是 i ，大家不要介意

如果函数f(x)不是绝对可积的，意味着其值在某些区域上可能过大，导致上述积分发散，从而傅里叶变换无法收敛。所以例如某些震荡性非常强的函数（比如正弦函数在整个无限区间上的积分），这种通常就不能直接做傅里叶变换。

好啦，简单总结一下：

• 绝对可积性：函数的绝对值的积分是有限的
• 傅里叶变换条件：绝对可积性确保傅里叶变换的积分收敛，变换结果存在且有意义