目录
一、实验内容
a) 介绍
在这次实验中,你将熟悉 Logisim 的操作流程,并且学习如何通过画图的方法 设计出计算机当中的核心运算器件——ALU。 然后,我们将使用七段数码管进一 步地人性化地显示出 ALU 的计算结果。
b) 复用器设计
算术逻辑单元(ALU)往往使用多个复用器,在多个功能之间进行切换,如下图所示:

在这部分实验中,你只需保留加法器和减法器的功能,即下图当中的红框部分:

设计一个 2:1 复用器,使得用户能够在 A+B 和 A-B 之间进行功能切换(操作数 A 和
B 均为 2 比特补码数)。
c)使用七段数码管显示二比特加法器对无符号数的计算结果
如下图所示,一个七段数码管中含有 7 个发光二极管,每一个发光二极管是一
个“段”,并分别被标注从 a 到 g 七个字母:

如下图所示,十六进制数当中的 0 至 F 可以使用一个七段数码管表示出来

比如,如果要显示数字 0,只需要点亮除 g 之外的所有段。
七段数码管需要搭配一个译码器才能正常使用。通常,一个七段数码管译码器
具有 4 比特输入 D3:0(可以表示一个从 0 至 F 的 16 进制数)和 7 比特输出 Sa:g(可
以驱动数码管)。它的原理图如下图所示:

为了设计这个七段译码器,你需要首先完成它对应的真值表。下表展示了 7 段数码
管的真值表

比如,当输入 D3:0 = 0000,除了 g 之外的所有段会被点亮。由于我们的七段数码
管是用高电平点亮,因此对应的 Sa:g = 1111110。当你完成真值表后,你可以推导
出相应的逻辑表达式并完成其数字电路实现。从 Sa 到 Sg 一共对应 7 个逻辑表达式,
课本已经为我们完成了其中两个(利用了无关项):

有了逻辑表达式之后,你将可以实现一个显示译码器,并利用 Logisim 提供的七段数码管显示加法器对两个无符号数的加法结果。
二、实验步骤
2.1 复用器的设计
(1)电路原理图:

(2)步骤
① 先利用复用器的真值表推断出复用器的逻辑表达式:Y=NOT(F)C0+FC1。
连接电路设计出一个复用器,如下图所示:

② 将此复用器封装好。
③ 利用c)中设计的2bit加法器,在A0、A1处连入A的值,在B0、B1处连入B的值。在
S0、S1、Cout分别连入输出。Cin处连入选择功能F(F=0为加法,F=1为减法)。利用上面设计
的复用器在C0处连入B0和B1的值,C1处连入NOT(B0)和NOT(B1)的值。用来实现减法功能。
④ 当F=0时,是实现加法功能,则B的值是B1B0,实现A+B.
⑤ 当F=1时,是实现减法功能,则选择B的值为NOT(B1)NOT(B0),实现A-B=A+NOT(B)+1。
2.2 七段数码管的设计
(1)电路原理图

(2)步骤
(1)利用真值表推导出Sa到Sg的逻辑表达式(无利用无关项):
Sa = ~D[2]⋅~D[0]+~D[3]⋅D[1]+~D[3]⋅D[2]⋅D[0]+D[3]⋅~D[2]⋅~D[1]+D[2]⋅D[1]
Sb = ~D[3]⋅~D[1]⋅~D[0]+~D[3]⋅D[1]⋅D[0]+~D[2]⋅~D[0]+D[3]⋅~D[1]⋅D[0]+~D[3]⋅~D[2]
Sc = ~D[3]⋅D[2]+D[3]⋅~D[2]+~D[1]⋅D[0]+~D[3]⋅~D[1]+~D[3]⋅D[0]
Sd = D[2]⋅~D[1]⋅D[0]+~D[2]⋅D[1]⋅D[0]+~D[3]⋅~D[2]⋅~D[0]+~D[3]⋅D[1]⋅~D[0]+~D[2]⋅~D[1]⋅~D[0]+D[3]⋅~D[1]⋅~D[0]+D[2]⋅D[1]⋅~D[0]
Se = ~D[2]⋅~D[0]+D[1]⋅~D[0]+D[3]⋅D[1]+D[3]⋅D[2]
Sf = ~D[3]⋅D[2]⋅~D[1]+D[3]⋅~D[2]+D[3]⋅D[1]+~D[3]⋅~D[1]⋅~D[0]+~D[3]⋅D[2]⋅~D[0]
Sg = ~D[2]⋅D[1]+D[2]⋅~D[1]+D[3]+D[1]⋅~D[0]
(2)利用“组合分析”输入正确的真值表,设计出七段译码管。
(3)利用七段译码管设计出七段数码管。如下图:

(4)利用c)中设计的2bit全加器和七段数码管来实现显示两个无符号数的加法结果。在加法器的结果输出时,要用一个分离器将1bit的结果转化为4bit的结果,传到七段译码管的输入端口。整体的电路设计图如下:

三、调试过程
3.1 复用器调试过程
eg.1 实现1+1(A:01,B:01,F:0)

如图所示,结果为2(010),答案正确。
eg.2 实现1+2(A:01,B:10,F:0)
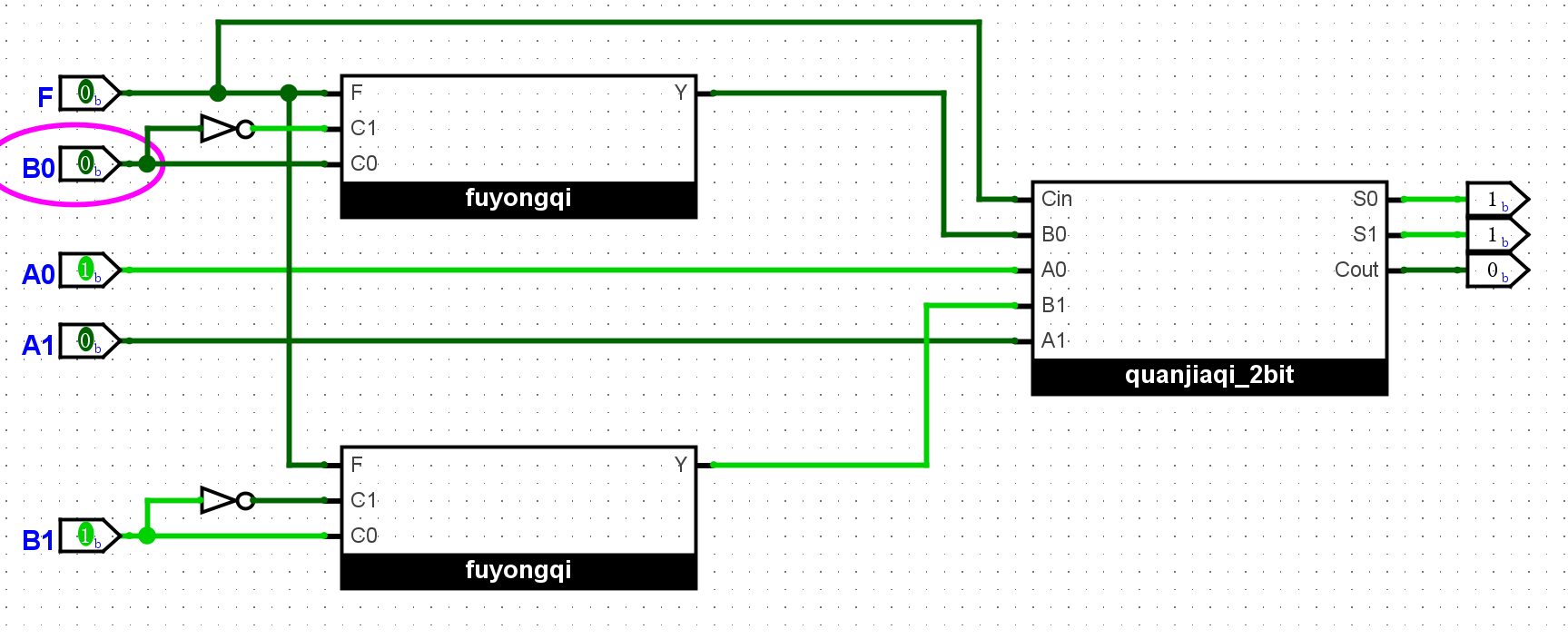
如图所示,结果为2(010),答案正确。
eg.3 实现1+2(A:01,B:10,F:0)

如图所示,结果为3(011),答案正确。
eg.4 实现3+2(A:11,B:10,F:0)

如图所示,结果为5(101),答案正确。
eg.5 实现2-1(A:10,B:01,F:1)

如图所示,结果为1(01(舍去Cout位)),答案正确。
eg..6 实现1-2(A:01,B:10,F:1)

如图所示,结果为-1(补码011变成原码101),答案正确。
eg.7 实现1-3(A:01,B:11,F:1)

如图所示,结果为-2(补码010变成原码110),答案正确。
3.2 七段数码管的调试过程
eg.1 实现1+1(A:01,B:01)

如图所示,结果为2,答案正确。
eg.2 实现2+2(A:10,B:10)

如图所示,结果为4,答案正确。
eg.3 实现3+3(A:11,B:11)

如图所示,结果为6,答案正确。
四、实验使用环境
本实验采用 Logisim 电路仿真平台。在使用 Logisim 设计本实验要求的数字电路的时候,
必须使用基本的逻辑门完成设计,而不允许使用 Logisim 提供的运算器(如封装好的加法
器、复用器或带译码器的七段数码管)
五、实验小结和思考
(1)收获
①掌握了复用器(MUX)的设计方法,实现加减法功能切换(F=0加法,F=1减法)。
②通过补码转换(A-B = A + ~B + 1)将减法统一为加法运算,简化了硬件设计。
③完成七段数码管译码器,能将4位二进制数转换为对应的段选信号,直观显示无符号数结果。
(2)关键问题与解决
①复用器逻辑混淆:初期误将功能选择信号F直接输入加法器,修正后通过MUX切换B和~B的输入。
②补码范围错误:误认为2bit补码范围为-1~2,经调试确认实际为-2~1(10为-2,01为1)。
③数码管显示异常:未处理进位输出(Cout),导致显示溢出值错误,后增加分离器分离有效位。























 2768
2768

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








