行列式的定义和按行展开

       行列式，线性代数基础中的基础，它的是所有不同行不同列的元素乘积的和，而每一项前的正负号由它列的逆序数  t  决定，即:，（排列中i和j不能重复）

       当我们知道它的定义后就求解一个行列式了，例如最简单的二阶行列式，如下:

                                                                    

       我们可以根据定义求得此处行列式的值就为,即1*4-2*3=-2。

       同样我们也能够通过定义求较为复杂的三阶行列式，如下:

                                                                 

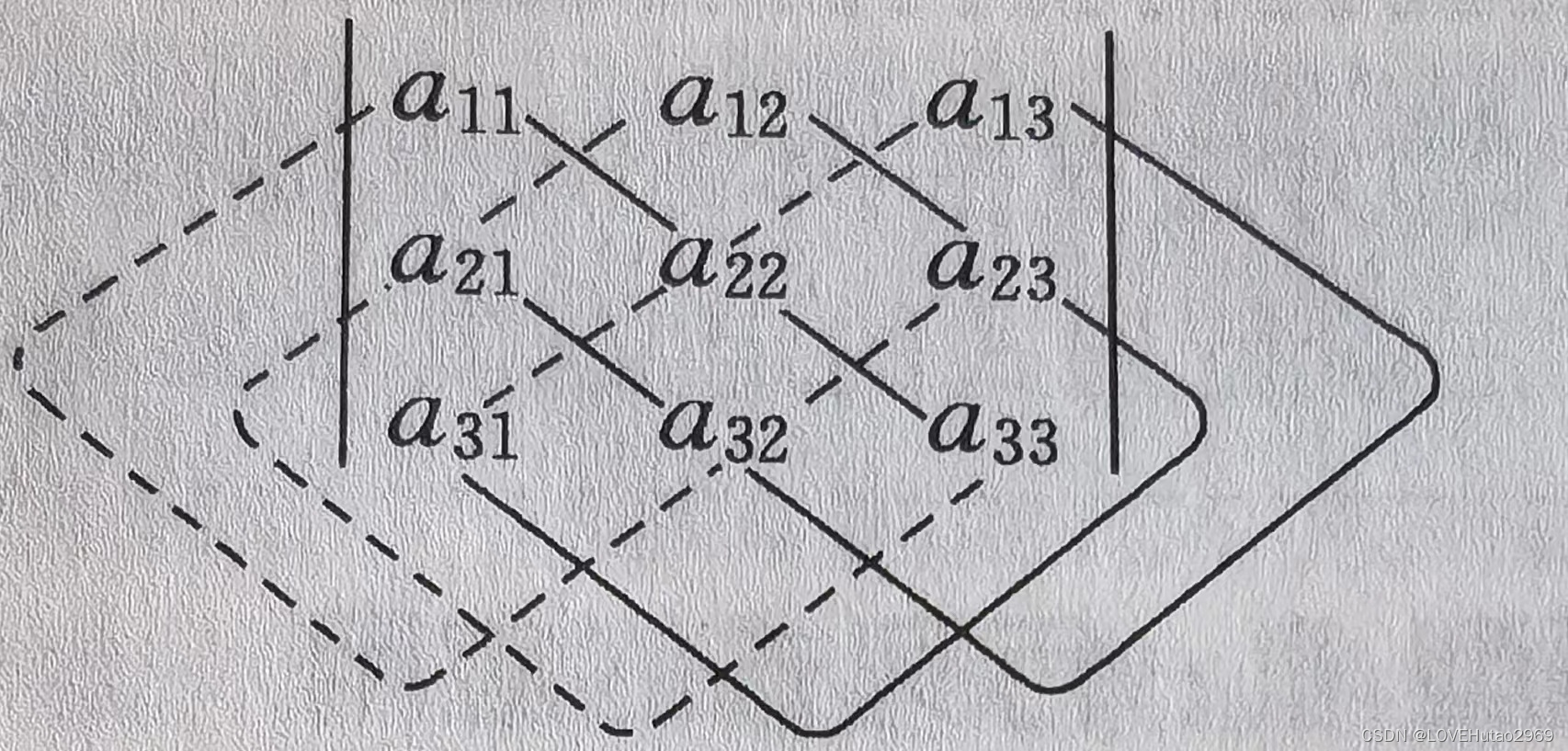
         根据定义为了方便运算我们总结出了一个规律,那就是画三角形（画三角形只有三阶时可用）

         因此此时我们选择用画三角形来求解，实现为加虚线为减，因此我们可以得到上面的行列式的值就是:即:

              1*5*9+3*4*8+2*6*7-3*5*7-2*4*9-1*6*8 = 45+96+84-105-72-48 = 0

       可是当我们遇到四阶即以上的行列式时，使用定义计算就变得非常复杂繁琐，因此我们总结出了几个性质和特殊的行列式以及几个结论。

       几种特殊的行列式:

       ①：对角或副对角行列式，分别为和如下：                                                                                                              

       ②：上三角行列式和下三角行列式的值为    如下：

                                                                   

       几个常用的性质和结论：

      性质一：行列式与它的转置相等

                                              

       性质二：行列式交换两行（列）变为行列式的负数

                                          

       性质三：行列式某一行（列）乘k可以将其提出行列式

                                         

       性质四：行列式某一列（行）的元素都是两数之和，则可以写成两个行列式相加

                          

       性质五：第i行（或第j列）乘k加到任意一行（或一列）值不变        

                         

        结论一:行列式中有一行为0行列式值为0

                                                         

       结论二：行列式两行成比例，则行列式为0

                                                    

       除此之外我们还可以利用行列式的按行展开来求行列式的值，

       行列式的按行展开

        行列式的按行展开就是将行列式的第n行的元素先提取出来，然后再根据定义求，可以理解为（a1+a2+a3）x = a1x+a2x+a3x。而将第一行分开后剩下的部分(也就是去掉第i行第j列的部分)就是余子式，代数余子式就是余子式前加上,如下所示:

           

其中就是其中一个余子式(M)，而就是其中一个代数余子式(A)。

并且我们可以推得（其实下面就相当于把第一行用第二行替换，使第一第二行相等，行列式为0）

 

       根据按行展开求余子式之和

        例如下面的行列式要我们求第一行各元素余子式之和：

        

      因为 ，所以我们可以将原式中第一行替换为

1，-1，1。如下:

        

       此时我们就可以通过求行列式的值来求最开始的行列式中余子式的和了

说明：由于我们只需要求余子式的和，因此第一行对我们来说可有可无，这时候如果我们将第一行替换成别的值，使行列式的值就是余子式的和，此时过程就被简化了！