深度学习模型：人工神经网络（ANN）详解

一、引言

在当今科技飞速发展的时代，深度学习无疑是最热门的领域之一。而人工神经网络（ANN）作为深度学习的基础模型，正深刻地改变着我们处理信息、理解世界的方式。从图像识别到语音助手，从自然语言处理到医疗诊断，ANN 的应用无处不在。在这篇博客中，我们将深入探讨 ANN 的出现历史、原理以及实现方法。

二、ANN 的出现历史

人工神经网络的发展历程源远流长，其根源可以追溯到上世纪中叶。早期的神经网络研究受到生物学中神经元结构和功能的启发，科学家们试图模拟人类大脑的信息处理方式。

在 20 世纪 40 年代，Warren McCulloch 和 Walter Pitts 提出了第一个人工神经元模型，它能够对输入信号进行简单的逻辑运算，这为神经网络的发展奠定了理论基础。[此处可配一张早期神经元模型的示意图，展示简单的输入输出逻辑关系]

随后，在 1958 年，Frank Rosenblatt 发明了感知机（Perceptron）。感知机是一种简单的线性分类模型，它能够通过调整权重来对输入数据进行分类。感知机的出现引起了广泛关注，人们对神经网络的发展充满了期待。[插入感知机模型的图片，展示其结构和数据流向]

然而，在 1969 年，Marvin Minsky 和 Seymour Papert 指出了感知机的局限性，即它无法处理复杂的非线性问题，这一观点使得神经网络的研究陷入了低谷。

直到 20 世纪 80 年代，随着计算能力的提升和反向传播算法的提出，神经网络研究迎来了新的曙光。反向传播算法有效地解决了多层神经网络的训练问题，使得神经网络能够学习到更加复杂的函数关系。这一时期，Hopfield 网络、自组织映射等多种神经网络模型相继被提出，神经网络的研究再次蓬勃发展。[配一张反向传播算法流程图的图片，帮助读者理解算法过程]

近年来，随着大数据时代的到来和 GPU 计算的普及，神经网络得到了前所未有的发展机遇。深度神经网络（DNN），即包含多个隐藏层的 ANN，在众多领域取得了惊人的成果，推动了人工智能技术的快速进步。

三、ANN 的原理

（一）基本结构

ANN 主要由输入层、隐藏层和输出层组成。输入层负责接收外部数据，例如一张图像的像素值、一段文本的词向量等。隐藏层是神经网络的核心部分，它包含多个神经元，这些神经元通过权重连接相互传递信息。输出层则根据隐藏层的处理结果生成最终的输出，比如图像分类任务中的类别标签、预测任务中的数值结果等。

（二）神经元与激活函数

每个神经元都接收来自上一层神经元的输入，并通过加权求和的方式进行处理。然后，将求和结果输入到激活函数中，激活函数的作用是引入非线性因素，使得神经网络能够处理复杂的非线性关系。常见的激活函数有 Sigmoid 函数、ReLU 函数等。Sigmoid 函数将输入值映射到 0 到 1 之间，常用于二分类问题；ReLU 函数则在输入大于 0 时输出输入值，小于 0 时输出 0，它能够有效缓解梯度消失问题，在深度学习中被广泛应用。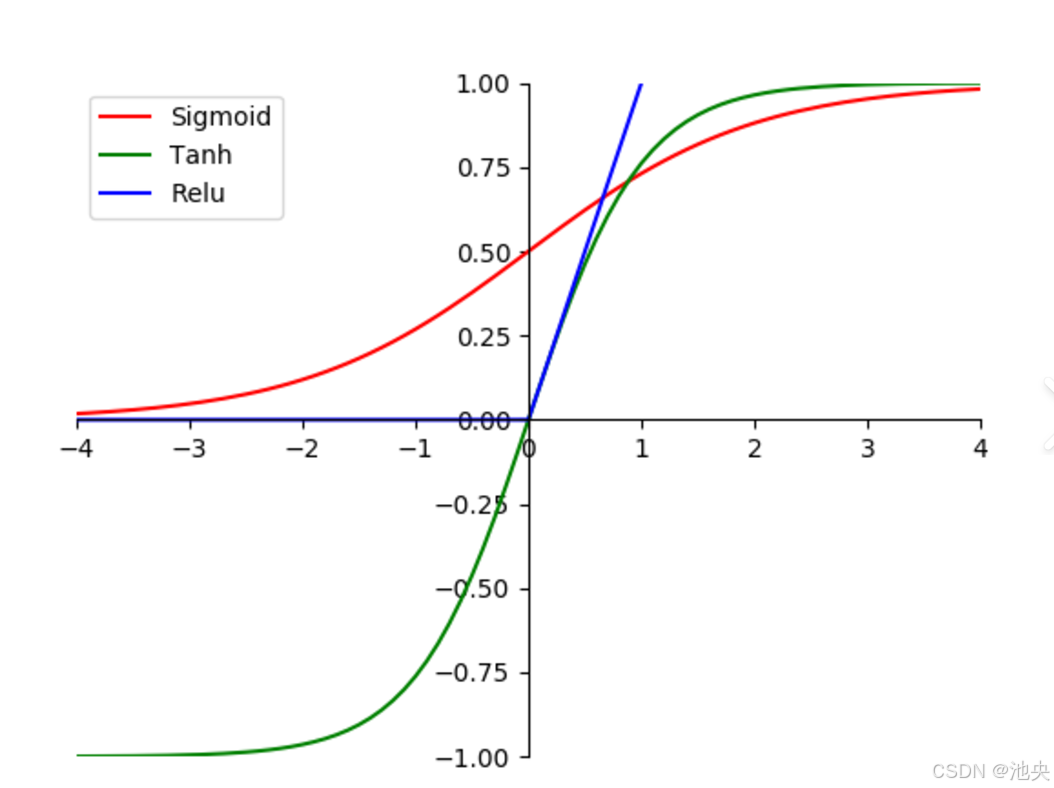

（三）前向传播与反向传播

在前向传播过程中，数据从输入层依次经过隐藏层，最终到达输出层。每一层的神经元根据输入和权重计算输出，并将结果传递给下一层。而在反向传播过程中，根据输出层的误差，通过链式法则依次计算每一层的误差，并根据误差调整权重。这个过程不断迭代，直到网络的损失函数达到最小值，从而使网络能够学习到输入数据的特征和模式。

（三）构建模型

使用选定的编程框架构建 ANN 模型。首先定义输入层的维度，然后添加隐藏层，并指定隐藏层的神经元数量、激活函数等参数，最后定义输出层。例如，在 TensorFlow 中可以使用 Keras 模块来快速构建模型：

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

# 构建模型
model = Sequential()
model.add(Dense(64, activation='relu', input_dim=100))  # 第一个隐藏层
model.add(Dense(32, activation='relu'))  # 第二个隐藏层
model.add(Dense(1, activation='sigmoid'))  # 输出层

（四）训练模型

定义好模型后，需要使用训练数据对其进行训练。这包括选择合适的损失函数（如交叉熵损失函数、均方误差损失函数等）和优化器（如随机梯度下降、Adam 优化器等），然后调用模型的训练函数进行训练。在训练过程中，可以设置训练的轮数、批次大小等参数，并监控训练过程中的损失值和准确率等指标。

# 编译模型
model.compile(loss='binary_crossentropy',
              optimizer='adam',
              metrics=['accuracy'])

# 训练模型
model.fit(x_train, y_train, epochs=10, batch_size=32,
          validation_data=(x_val, y_val))

（五）评估与预测

训练完成后，使用测试集对模型进行评估，计算模型的准确率、召回率、F1 值等指标，以评估模型的性能。同时，还可以使用训练好的模型对新的数据进行预测。

# 评估模型
loss, accuracy = model.evaluate(x_test, y_test)

# 预测
predictions = model.predict(x_new)