微分中值定理与导数的应用

微分中值定理

一、罗尔定理 

        在谈论罗尔定理之前，我们先了解一下费马定理。 

        费马定理：设函数f(x)在点x的某邻域U(x0)内有定义,并且在x0处可导，如果对任意的xU(x0),有，那么

        此定理可以简单记为:极值点处的导函数为0。

        费马定理的几何意义:若x为函数f(x0)的一个极值点，则函数在点(x0,f(x0))处的切线一定与x轴平行。
 

        罗尔定理：

 

         

证明罗尔定理

例题

    

二、拉格朗日中值定理 

 

证明拉格朗日中值定理 

此处所构造的函数的意义：

        目的是找两个端点相等，构造的函数是φ（x）是曲线与直线的差值；而L（x）是利用点斜式建立的直线方程

常用形式

                                         

                         

        自变量取得有限增量x（x不一定很小），函数增量y的准确表达式如上；在某些问题中当自变量x取得有限增量x而需要函数增量的准确表达式时，拉格朗日定理就显出它的价值。

定理一

        若函数f（x）在区间I上连续，I内可导且导数恒为0，那么f（x） 在区间I上是一个常数。

证明定理一 

 例题

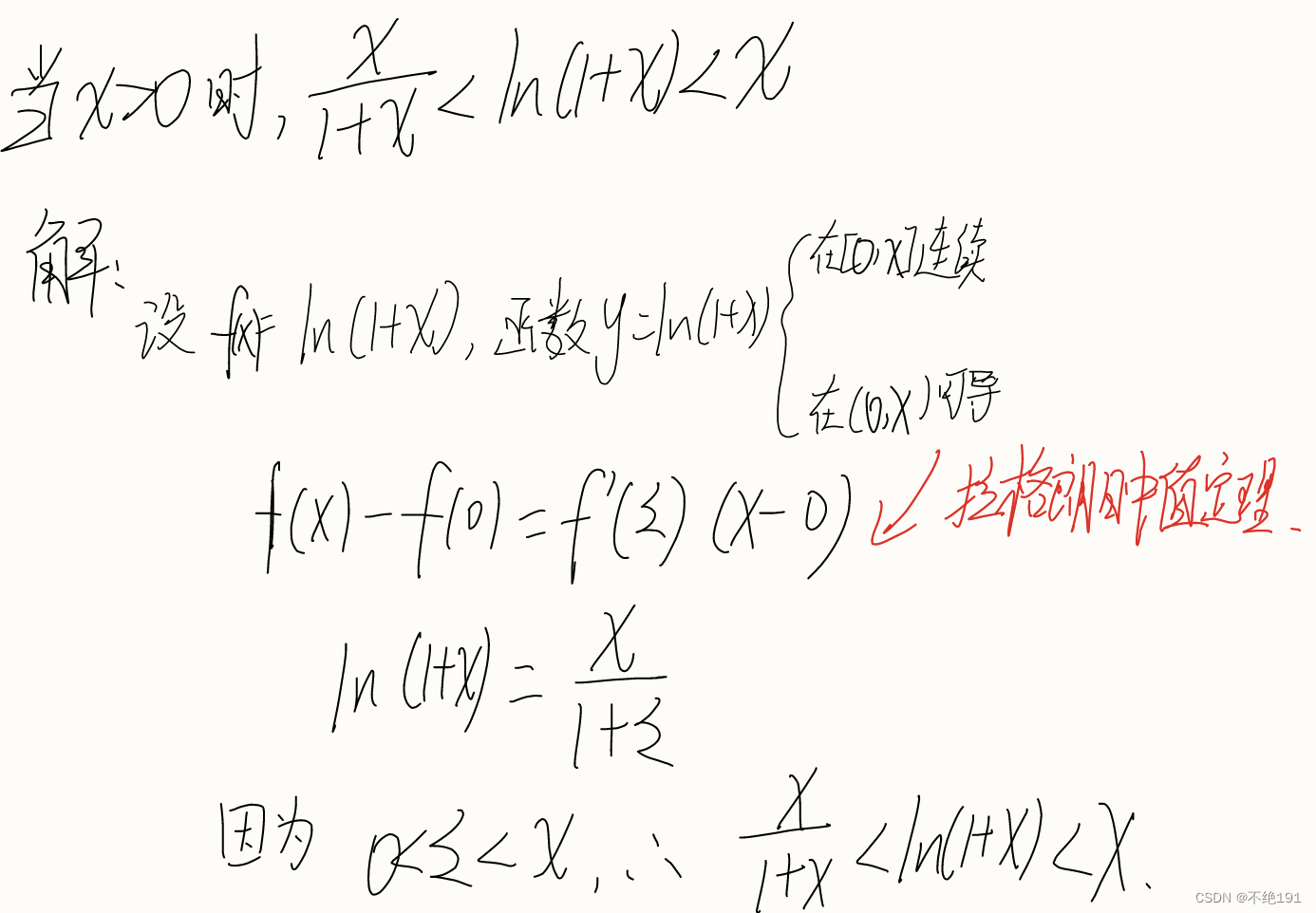
三、柯西中值定理 

        函数在参数方程形式下的拉格朗日中值定理的表达形式，通过这个问题可以得到以下结论。

 

证明柯西中值定理

  

洛必达法则

一、“0/0”型不定式      

证明柯西中值定理

 例题  

 二、“无穷/无穷”型不定式

三、其他型的不定式 

  例题  

泰勒公式 

        泰勒公式的本质是近似，用更高次的幂函数来近似于任意函数。

泰勒公式一 

泰勒公式二 

         泰勒公式一中的Rn(x)不能具体估算出误差的大小，而下面给出的具有另一种余项形式的泰勒定理则解决了这一问题。

 麦克劳林公式

        使用泰勒定理展开，但是假设起始点x0=0。

几个常见函数的泰勒展开 

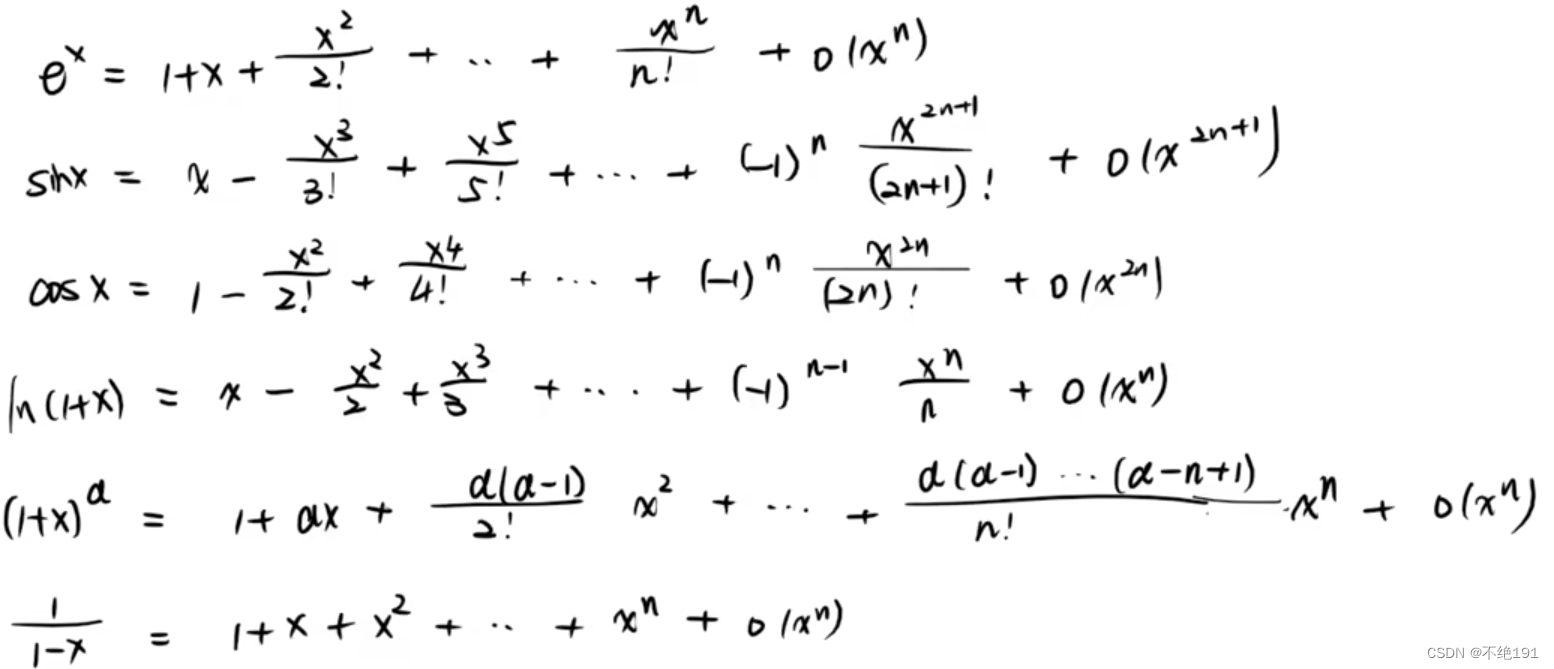
 例题  

函数的单调性与曲线凹凸性 

函数单调性的判定法 

          

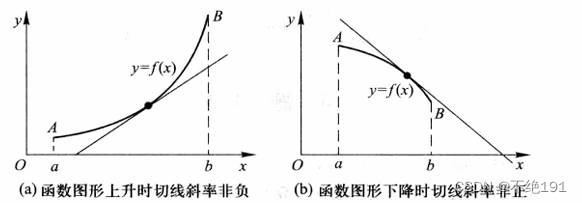
  例题  

         这个定理即可以判断函数单调区间，又可以构造函数来验证不等式。 

 

曲线的凹凸性与拐点 

         通过上述关系式可推出如下定理：

拐点

        

 例题  

函数的极值与最值 

函数的极值与求法 

        函数的极大值和极小值的概念是局部性的。

        极值定义：设函数f（x）在点x0的某邻域中有定义，在邻域中任意x有或者，那么就称f（x0）是函数f（x）的极大值（或极小值）。 

         

        判断极大值与极小值的充分条件： 

        当函数f（x）在驻点处的二阶导数存在且不为0时，也可以用下述定理来判定f（x）在驻点处是极大值还是极小值

最大值与最小值问题 

        首先，根据闭区间上连续函数的性质可知，f（x）在[a，b]上的最大值和最小值一定存在，最值即有可能是极值，也可能在区间的端点处取得最值。

         因此，可用如下方法求f（x）在[a，b]上的最大值和最小值。

  例题  

描绘函数图像         

渐近线

一、水平渐近线 

二、垂直渐近线 

三、斜渐近线 

  例题   

 描绘图像的步骤

 例题 

曲率 

弧微分 

        弧微分是微积分中的一个重要概念，它是用来描述平面上或空间中某曲线局部的一小段弧长的微小增量。

        如果给定一条由连续可微函数 y=f(x) 定义的曲线，那么在这条曲线上任意一点M(x,y)，我们可以用一个小线段Δs近似地代替曲线上的微小弧长。 

弧微分的三个公式

曲率及其计算公式 

        曲率表示弧线的弯曲程度。

影响曲率的因素 

证明曲率的计算 

  例题 

 

曲率圆与曲率半径  

        与曲线上一点的切线相切的圆叫做曲率圆。 

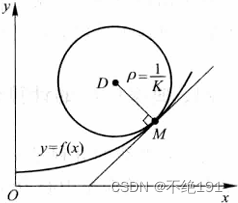
        如上图所示，曲率圆的圆心D叫做曲线在点M处的曲率中心，曲率圆的半径p叫做曲线在点M处的曲率半径。曲率圆与曲线在点M有相同的切线和曲率。

        曲率K与曲率半径P有如下关系：

         

  例题 

 

曲率中心的计算公式  渐屈线与渐伸线

曲率中心计算式 

        设已知曲线方程是y=f（x），曲线在对应点M（x，y）的曲率中心D（a，b）的坐标如下

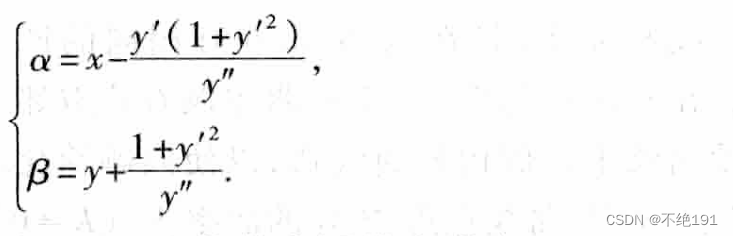
渐屈线与渐伸线 

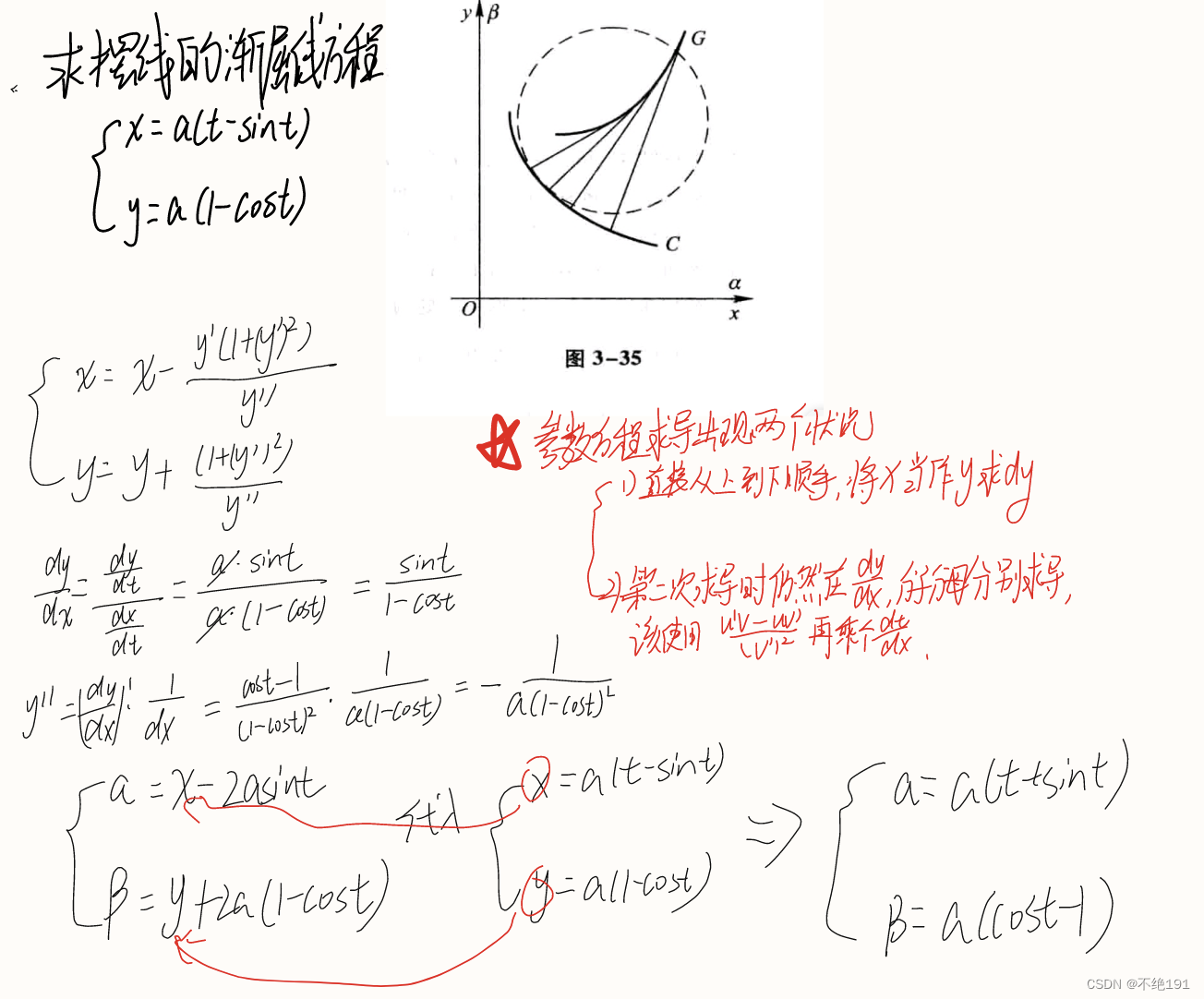
         当点（x，y）沿曲线C移动时，相应的曲率中心D的轨迹曲线G称为曲线C的渐屈线，而曲线C称为曲线G的渐伸线。渐屈线的参数方程为

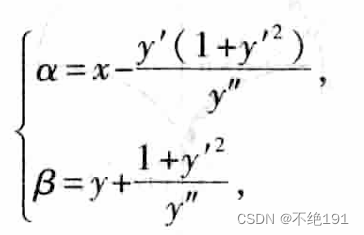
例题