实验内容
问题1:取k=2,3,4,5,6 来对IRIS数据集进行k-means分析,比较结果,找出结果中的相似性和不同。
问题2:设计程序实现通过CH指数来计算动态聚类 聚类数的优化(以IRIS数据为例),给出IRIS的最优聚类数。
问题3:不同的距离对层次聚类的结果有影响吗?
问题1
1.1 问题描述与分析
在进行 k-means 分析时,选择适当的 k 值 非常重要。如果 k 值过小,可能会将不同类别的数据聚合到一起,导致聚类结果不准确;如果 k 值过大,可能会将同一类别的数据分成多个簇,导致聚类结果过于细化。我们选择了 IRIS 数据集进行分析,首先从 k 取值范围为 2 到 6 的情况下,通过直观的解释和分析来确定最合适的 k 值。
为了更直观地感受聚类的过程,我们选择 IRIS 数据集的两列特征进行可视化展示。
1.2 代码
# +++++++++++++代码1+++++R工具包(含CH指数的计算)+++++++++++++
# 定义一个函数 kclust,用于执行 K-means 或 K-medoids 聚类
# 添加函数ch.index用于计算ch指数
# 参数:
# x: 数据矩阵,n 行代表观测值,p 列代表特征。
# centers: 向量,给出起始中心点。默认为 NULL,此时我们会随机选择 k 个中心点。
# k: 聚类数量。如果指定了 centers 参数,则不需要指定 k。
# alg: 算法。可以是 "kmeans" 或 "kmedoids"。默认为 "kmeans"。
# maxiter: 最大迭代次数。默认为 100。
# kmax:k的最大值
# iter.max:迭代的最大次数,默认为100,
# nstart:初始的点的个数,默认为10
# algorithm :默认为"Lloyd"、
# 返回:
# centers: 长度为 k 的向量,给出最终的中心点。
# cluster: 长度为 n 的向量,给出最终的聚类分配。
# iter: 执行的迭代次数。
# cluster.history: 维度为 iter × k 的矩阵,每行给出对应迭代的聚类分配。
kclust = function(x, centers=NULL, k=NULL, alg="kmeans", maxiter=100) {
n = nrow(x)
p = ncol(x)
if (is.null(centers)) {
if (is.null(k)) stop("Either centers or k must be specified.")
if (alg=="kmeans") centers = matrix(runif(k*p,min(x),max(x)),nrow=k)
else centers = x[sample(n,k),]
}
k = nrow(centers)
cluster = matrix(0,nrow=0,ncol=n)
for (iter in 1:maxiter) {
cluster.new = clustfromcent(x,centers,k)
centers.new = centfromclust(x,cluster.new,k,alg)
cluster = rbind(cluster,cluster.new)
j = is.na(centers.new[,1])
if (sum(j)>0) centers.new[j,] = centers[j,]
centers = centers.new
if (iter>1 & sum(cluster[iter,]!=cluster[iter-1,])==0) break
}
return(list(centers=centers,cluster=cluster[iter,],iter=iter,cluster.history=cluster))
}
# Compute clustering assignments, given centers
clustfromcent = function(x, centers, k) {
n = nrow(x)
dist = matrix(0,n,k)
for (i in 1:k) {
dist[,i] = colSums((t(x)-centers[i,])^2)
}
return(max.col(-dist,ties="first"))
}
# Compute centers, given clustering assignments
centfromclust = function(x, cluster, k, alg) {
if (alg=="kmeans") return(avgfromclust(x,cluster,k))
else return(medfromclust(x,cluster,k))
}
avgfromclust = function(x, cluster, k) {
p = ncol(x)
centers = matrix(0,k,p)
for (i in 1:k) {
j = cluster==i
if (sum(j)==0) centers[i,] = rep(NA,p)
else centers[i,] = colMeans(x[j,,drop=FALSE])
}
return(centers)
}
medfromclust = function(x, cluster, k) {
p = ncol(x)
centers = matrix(0,k,p)
for (i in 1:k) {
j = cluster==i
if (sum(j)==0) centers[i,] = rep(NA,p)
else {
d = as.matrix(dist(x[j,],diag=T,upper=T)^2)
ii = which(j)[which.min(colSums(d))]
centers[i,] = x[ii,]
}
}
return(centers)
}
# Compute within-cluster variation
wcv = function(x, cluster, centers) {
k = nrow(centers)
wcv = 0
for (i in 1:k) {
j = cluster==i
nj = sum(j)
if (nj>0) {
wcv = wcv + sum((t(x[j,])-centers[i,])^2)
}
}
return(wcv)
}
# 定义计算 Calinski-Harabasz (CH) 指数的函数
ch.index <- function(x, kmax, iter.max = 100, nstart = 10, algorithm = "Lloyd") {
ch <- numeric(length = kmax - 1) # 初始化一个长度为 kmax - 1 的数值向量 ch,用于存储每个 k 对应的 CH 指数
n <- nrow(x) # 观测值的数量
for (k in 2:kmax) {
km <- kmeans(x, centers = k, iter.max = iter.max, nstart = nstart, algorithm = algorithm) # 使用 kmeans 算法进行聚类
# 总平方和
tss <- sum((x - matrix(colMeans(x), nrow = n, ncol = ncol(x), byrow = TRUE))^2) # 计算总平方和
# 类间平方和
bss <- sum(sapply(unique(km$cluster), function(cl) {
sum(nrow(x[km$cluster == cl, , drop = FALSE]) * (colMeans(x[km$cluster == cl, , drop = FALSE]) - colMeans(x))^2)
})) # 计算类间平方和
# 类内平方和
wss <- tss - bss # 计算类内平方和
# CH指数
ch[k - 1] <- (bss / (k - 1)) / (wss / (n - k)) # 计算 CH 指数并存储在 ch 中
}
return(list(k = 2:kmax, ch = ch)) # 返回包含 k 值和对应 CH 指数的列表
}
# +++++++++++++代码2++++++++++++++++++
# 加载kclust.R文件中的函数
source("kclust.R")
# 设置随机种子
set.seed(0)
# 加载IRIS数据集
data(iris)
# 提取iris数据集的前四列作为特征
x <- as.matrix(iris[,1:4])
# 选择前两列特征进行可视化
x = x[,1:2]
# TODO 2: 动态聚类并实现可视化
for (k in 2:6){
# 初始化聚类中心和颜色
cent.init = rbind(c(4.5, 2.5), c(4.5, 3.5), c(6.0, 2.5), c(6.0, 3.5), c(7.5, 2.5), c(7.5, 3.5))
cols = c("red", "darkgreen", "blue", "magenta", "green", "cyan")
cent.init <- cent.init[1:k, ]
cols <- cols[1:k]
# 绘制数据点和初始聚类中心
plot(x)
points(cent.init, pch = 19, cex = 2, col = cols)
# 运行k-means聚类算法
km1 = kclust(x, centers = cent.init, alg = "kmeans")
print(km1$iter)
# 绘制最终的聚类结果和聚类中心
plot(x, col = cols)
points(km1$centers, pch = 19, cex = 2, col = cols)
cent.old = cent.init
plot(x)
points(cent.old, pch = 19, cex = 2, col = cols)
par(ask = TRUE)
# 根据迭代次数逐步展示聚类过程
for (i in 1:km1$iter) {
plot(x, col = cols[km1$cluster.history[i,]], main = paste("Iteration", i))
points(cent.old, pch = 19, cex = 2, col = cols)
plot(x, col = cols[km1$cluster.history[i,]], main = paste("Iteration", i))
cent.new = centfromclust(x, km1$cluster.history[i,], k, alg = "kmeans")
points(cent.new, pch = 19, cex = 2, col = cols)
cent.old = cent.new
}
}
1.3 结果图
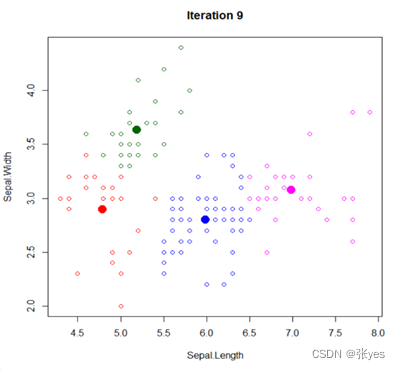
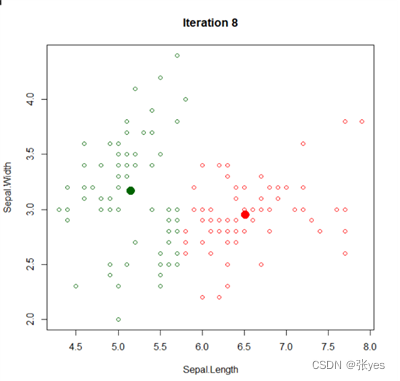 |  |
| K=2时的聚类图 | K=3时的聚类图 |
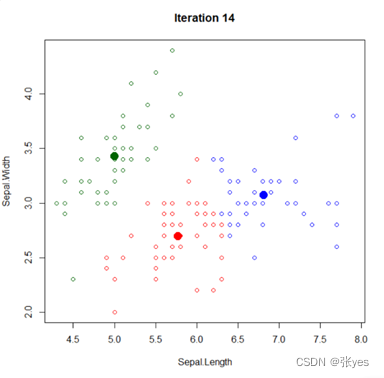
 | 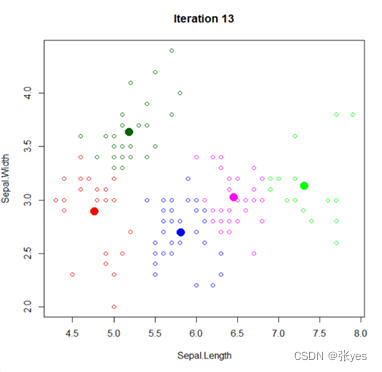 |
| K=4时的聚类图 | K=5时的聚类图 |
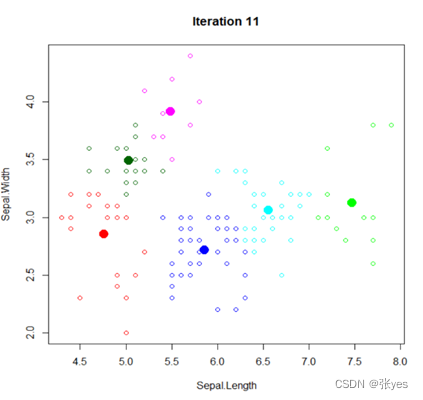 | |
| K=6时的聚类图 | |
| 图1:K=2,3,4,5,6时的IRIS数据集聚类图(部分特征) | |
1.4 异同
相同点:
1对于所有的k值,每个数据点都会被分配到一个簇中,不存在任意一个孤立的不属于任何簇的数据点。
2.每个簇都有且只有一个质心,该质心用于表示该簇的中心位置。
3.会发现某些簇之间的样本分布比较密集,而与其他簇之间的样本分布相对稀疏。
不同点:
1.不同的k值会导致不同的簇的数量和形状,这会影响到样本的分布情况。
2.不同的k值会导致不同的质心位置,从而影响到簇的划分结果。
3.不同的k值会导致不同的簇大小和样本分布情况。
4.不同的k值,k-means算法的迭代次数不尽相同,同时迭代次数也与初始点的选取有关。
问题2
2.1 问题描述与分析
为了避免主观选择k值而导致结果的不确定性,通常采用一些指标来帮助确定最佳的k值。其中一个常用的指标是CH指数,它可以帮助我们评估不同k值下的聚类性能。CH指数通过比较聚类内部的紧密度和聚类间的分离度来评估聚类的质量,值越大表示聚类效果越好。
对于IRIS数据集,我们可以计算不同k值下的CH指数,并选择CH指数最大的k值作为最优的聚类数。这样做可以尽量避免主观感受对k值的影响,而更加客观地选择合适的聚类数。
具体步骤包括:
对于给定的数据集,在一定范围内尝试不同的k值,比如从2到n(数据集样本数)之间的值。
对每个k值,使用K-means算法进行聚类,并计算CH指数。
选择CH指数最大的k值作为最优的聚类数。
这样就能够通过客观的指标来确定最佳的聚类数,而不是依赖于主观的感觉或经验。
2.2代码
# +++++++++++++代码三+++++ CH指数的计算,并实现可视化++++++++++++
# 加载kclust.R文件中的函数
source("kclust.R")
# 设置随机种子
set.seed(0)
# 加载IRIS数据集
data(iris)
# 提取iris数据集的前四列作为特征
x <- as.matrix(iris[,1:4])
# TODO : 计算CH指数并实现可视化
result <- ch.index(x, kmax = 6)
k_values <- result$k
ch_values <- result$ch
# 创建CH指数与簇数量之间的折线图
plot(k_values, ch_values, type = "o", xlab = "Number of Clusters (k)", ylab = "CH Index",
main = "CH Index vs. Number of Clusters", xlim = c(1.5, 6.5), ylim = c(410, 590))
points(k_values, ch_values, col = "blue", pch = 16)
text(k_values, ch_values, labels = round(ch_values, 2), pos = 4, col = "blue")
2.3结果图
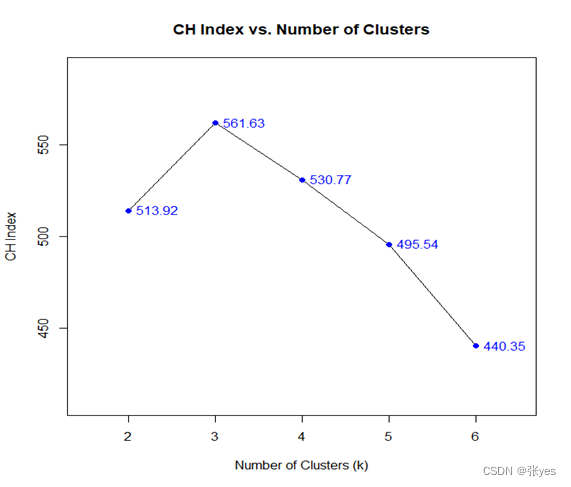 |
| 图2: CH指数折线图(iris数据集) |
2.4 分析
根据折线图,我们能看出来,当k=3时,CH指数达到最大值为561.63。这指示我们将IRIS数据集聚成三类是合适的选择。
问题3
3.1 问题描述与分析
不同的距离度量方式对层次聚类的结果会产生影响。这种影响的原因在于,距离度量方式决定了样本之间距离的计算方式,进而影响了聚类算法在构建聚类结构时如何评估样本之间的相似性或距离。这会直接影响到最终形成的聚类结构。
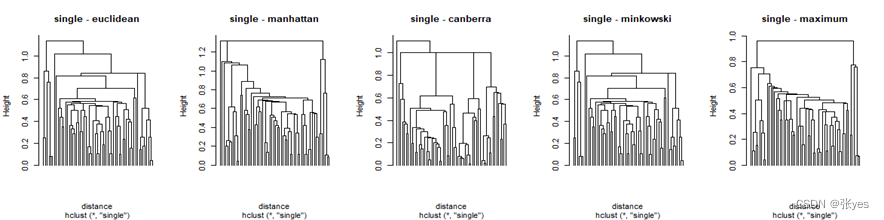
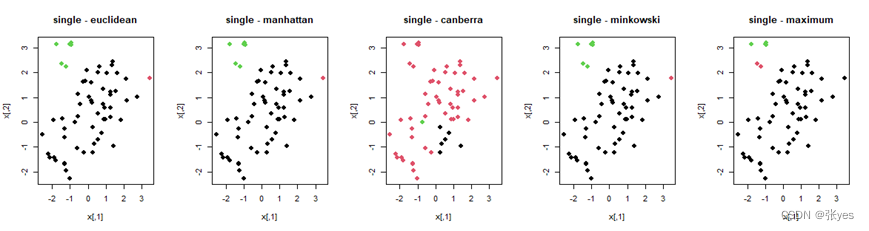
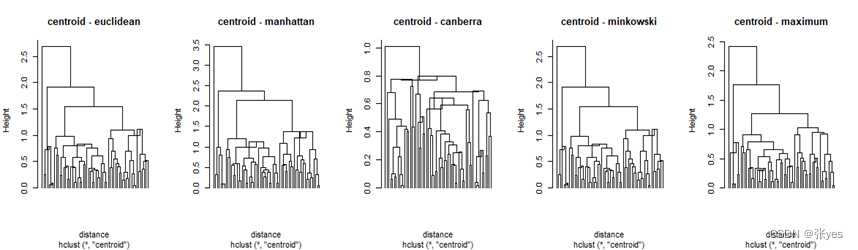
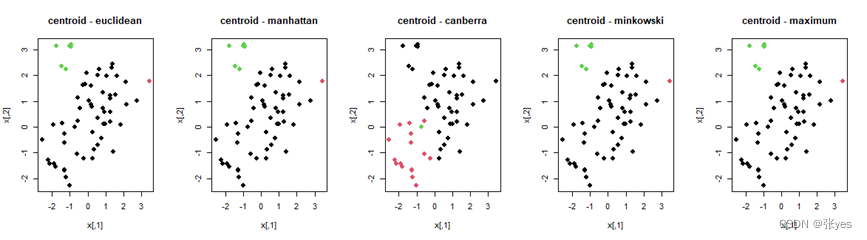
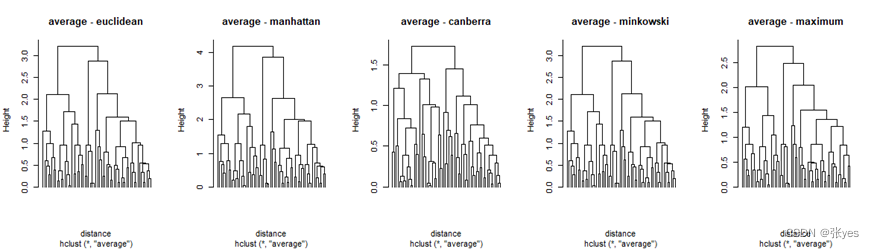
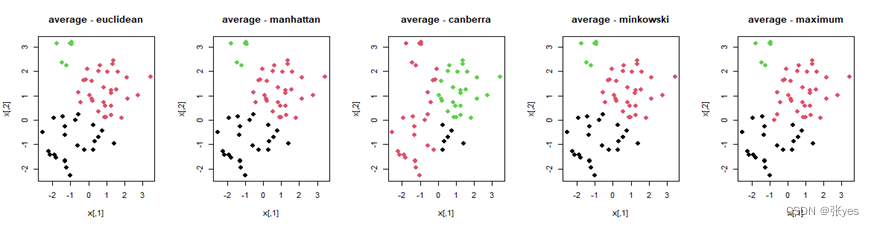
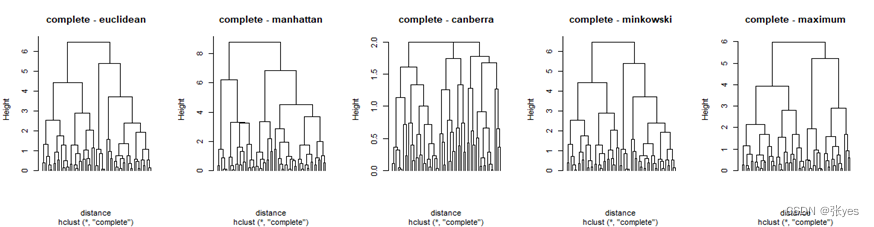
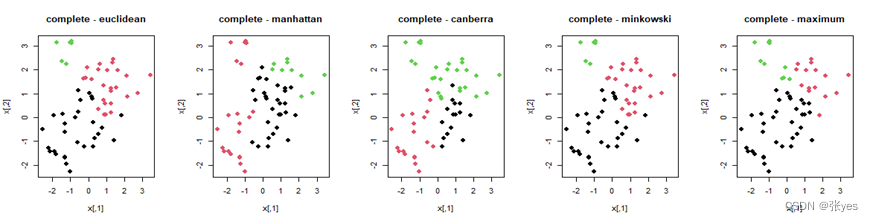
我选取了常见的5个距离("euclidean","manhattan","canberra,"minkowski","maximum")对该影响进行分析。同时为了尽可能减少linkage的影响,在同一个linkage(共5个linkage)下进行5种距离的比较。
3.2代码
# +++++++++++++代码四+++++层次聚类树可视化+++++++++++++
set.seed(0)
x = rbind(scale(matrix(rnorm(2*20),ncol=2),cent=c(1,1),scale=F), # 创建第一组数据并标准化
scale(matrix(rnorm(2*30),ncol=2),cent=-c(1,1),scale=F)) # 创建第二组数据并标准化
x = rbind(x,matrix(runif(2*10,min(x),max(x)),ncol=2)) # 添加第三组数据,范围与前两组相同
# 定义距离算法和链接方法
linkage_methods <- c("single", "complete", "average", "centroid")
distance_methods <- c("euclidean", "manhattan", "canberra", "minkowski","maximum")
# 欧氏距离 曼哈顿距离 兰氏距离 闵可夫斯基距离 最大距离
# Minimax法
par(mfrow=c(1,5)) # 设置绘图排列方式
# 循环计算并绘制不同距离计算方法的 Minimax 聚类树
for (i in 1:length(distance_methods)) {
distance <- dist(x, method = distance_methods[i]) # 计算距离
tree <- protoclust(distance) # 构建 Minimax 聚类树
plot(tree, main = paste("Minimax -", distance_methods[i]), labels = rep("", 60), hang = -1e-10) # 绘制聚类树
}
# 绘制 Minimax 聚类的散点图
for (i in 1:length(distance_methods)) {
distance <- dist(x, method = distance_methods[i]) # 计算距离
tree <- protoclust(distance) # 构建 Minimax 聚类树
labs <- cutree(tree, k = 3) # 切割树以获取聚类标签
# 根据聚类标签绘制散点图
plot(x, col = labs, pch = 20,cex = 2,main = paste("Minimax -", distance_methods[i])) # 绘制散点图
}
# 设置绘图排列方式
# 循环计算并绘制不同距离计算方法和链接方法的聚类树
for (i in 1:length(linkage_methods)) {
plot(x) # 绘制原始数据图
par(mfrow=c(1, 5))
for (j in 1:length(distance_methods)) {
distance <- dist(x, method = distance_methods[j]) # 计算距离
tree <- hclust(distance, method = linkage_methods[i]) # 构建聚类树
plot(tree, main = paste(linkage_methods[i], "-", distance_methods[j]), labels = rep("", 60), hang = -1e-10) # 绘制聚类树
}
readline("点击 Enter 键继续...") # 添加交互式提示,等待用户点击 Enter 键
}
# 循环计算并绘制不同距离计算方法和链接方法的散点图聚类
for (i in 1:length(linkage_methods)) {
plot(x) # 绘制原始数据图
par(mfrow=c(1, 5))
for (j in 1:length(distance_methods)) {
distance <- dist(x, method = distance_methods[j]) # 计算距离
tree <- hclust(distance, method = linkage_methods[i]) # 构建聚类树
labs <- cutree(tree, k = 3) # 切割树以获取聚类标签
# 根据聚类标签绘制散点图
plot(x, col = labs, pch = 20,cex = 2, main = paste(linkage_methods[i], "-", distance_methods[j])) # 绘制散点图
}
readline("点击 Enter 键继续...") # 添加交互式提示,等待用户点击 Enter 键
}3.3结果图
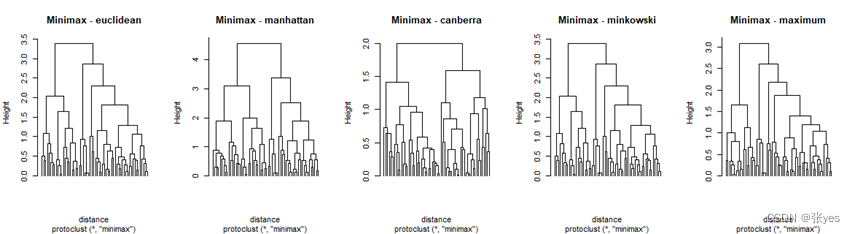 |
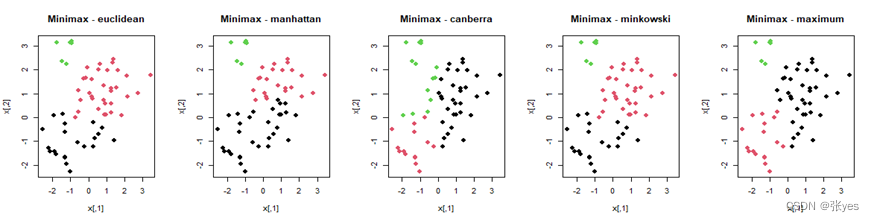 |
 |
 |
 |
 |
 |
 |
 |
 |
| 图3: 层次聚类树 散点图 |
3.4 分析
不同的距离对层次聚类的结果有影响
1.欧氏距离(Euclidean Distance):
欧氏距离是最常用的距离度量方法之一,它衡量了特征空间中两点之间的直线距离。
在聚类过程中,欧氏距离通常会形成球状的簇,适用于数据分布比较规则的情况。
在欧氏距离中,各个特征对距离的贡献是相等的,因此它适用于各个特征具有相似尺度的情况。
欧氏距离对异常值,离群点特别敏感,因为它计算了样本在每个维度上的差异的平方和。
2.曼哈顿距离(Manhattan Distance):
曼哈顿距离也称为L1 距离,它是通过沿着坐标轴的路径计算两点之间的距离。
曼哈顿距离对于特征之间的关联性不敏感,因此在某些情况下,它可以更好地处理具有不同尺度或不同分布的特征的数据。
曼哈顿距离对异常值的影响较小,因为它仅计算了各个维度上的绝对差异。
3.兰氏距离(Canberra Distance):
兰氏距离考虑了特征之间的比例关系,对于具有不同尺度的特征,它更为合适。
兰氏距离对异常值不太敏感,因此在数据中存在异常值的情况下,可以产生较为稳定的聚类结果。
兰氏距离适用于数据中存在较大变化的情况,尤其是当数据中有许多零值或接近零值时。
它对异常值不太敏感,但可能会受到数据中存在较小值的影响。
4.闵可夫斯距离(Minkowski Distance):
闵可夫斯距离是欧氏距离和曼哈顿距离的一般化,具有一个参数 p,当 p=2 时等同于欧氏距离,当 p=1 时等同于曼哈顿距离。
闵可夫斯距离在聚类过程中可以根据具体情况调节参数 p,以适应不同类型的数据分布和特征尺度。
闵可夫斯距离是欧式距离和曼哈顿距离的一般化,当p=2时就是欧式距离,当p=1时就是曼哈顿距离。
通过调整参数p,可以控制距离的敏感度。
5.最大距离(Maximum Distance):
最大距离也称为切比雪夫距离,它计算两个点之间的最大距离,即它们之间任意一维特征的差的绝对值的最大值。
最大距离对异常值非常敏感,在存在异常值的情况下,可能会导致聚类结果偏离真实情况。
最大距离度量方式,也称为切比雪夫距离,计算两个样本在所有维度上的最大差异。
它对异常值非常敏感,因为它只考虑了最大差异。
总体而言,不同的距离度量方式大致会导致以下影响:
距离的计算方式不同:不同的距离度量方式会以不同的方式计算样本之间的距离。例如,欧式距离考虑了各个维度上的差异的平方和,而曼哈顿距离则只计算了各个维度上的绝对差异之和。这样的差异会直接影响到样本之间的相似性度量,从而影响到聚类结果。
对异常值的敏感度不同:某些距离度量方式对异常值更为敏感,而另一些则相对不那么敏感。例如,欧式距离会受到异常值的影响,因为它计算了样本在每个维度上的差异的平方和,而曼哈顿距离则相对不太受到异常值的影响。
对数据分布特征的假设不同:不同的距离度量方式会对数据的分布特征作出不同的假设。例如,兰氏距离适用于数据中存在较大变化的情况,尤其是当数据中有许多零值或接近零值时,而欧式距离则适用于数据在高维空间中具有明显的凸性结构的情况。
因此,在选择距离度量方式时,需要考虑数据的特点以及聚类的目标。不同的距离度量方式可能会导致不同的聚类结果,因此需要根据具体情况选择最适合的距离度量方式,以获得更准确和有意义的聚类结果。
在选择距离度量方式时,需要考虑数据的特性以及聚类的目标。一般来说,需要根据具体情况来选择最适合的距离度量方式,以获得更准确和有意义的聚类结果。不能一概地去说明那个距离就绝对优于别的距离,优于只是针对于具体问题的具体需求而言。每一个距离的存在都是合理的。
总的来说,不同的距离度量方法会导致聚类结果的形成和簇之间的关系不同,选择合适的距离度量方法需要根据数据的特征、分布情况以及对异常值的处理要求进行考虑。这些距离度量方法在聚类过程中会影响簇的形成和样本之间的相似度计算。具体选用哪种方法取决于数据的特征、数据的分布情况以及对异常值的处理要求。





















 31万+
31万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








