如何估算 Transformer 模型中的参数数量

最新推荐文章于 2025-04-10 16:10:39 发布

大耳朵爱学习

最新推荐文章于 2025-04-10 16:10:39 发布

阅读量1.6k

点赞数 8

文章标签： transformer 深度学习人工智能机器学习大语言模型 LLM 自然语言处理

本文链接：https://blog.csdn.net/2401_85379281/article/details/142413322

版权

最有效的理解新机器学习架构（以及任何新技术）的方式是从零开始实现它。虽然这种方法非常复杂、耗时，并且有时几乎不可能做到，但它能帮助你深入理解每一个实现细节。例如，如果你没有相应的计算资源或数据，你将无法确保你的解决方案中没有隐藏的错误。

不过，还有一种更简单的方法——计算参数数量。相比直接阅读论文，这种方法并不复杂，但能够让你深入理解新架构的构建模块（在这里指的是 Transformer 编码器和解码器模块）。

你可以参考以下示意图来理解这一点，该图展示了三种理解新机器学习架构的方式——圆圈的大小代表对架构的理解程度。

理解机器学习架构的方式。计算参数数量并不比简单阅读论文难多少，但它能让你更深入地探究这个主题。图片由作者提供。

在本文中，我们将深入探讨著名的 Transformer 架构，并学习如何计算 PyTorch 中 TransformerEncoderLayer 和 TransformerDecoderLayer 类的参数数量。通过这种方式，我们将确保完全理解该架构的组成，不再有任何神秘之处。

我不仅提供了精确的公式，还提供了它们的近似版本，这将帮助你快速估算任何基于 Transformer 模型的参数数量。

Transformer 架构

著名的 Transformer 架构在 2017 年的突破性论文《Attention Is All You Need》中被提出，并凭借其有效捕捉长距离依赖的能力，成为大多数自然语言处理和计算机视觉任务中的事实标准。

在2023年初，扩散模型因文本到图像生成模型的广泛应用而极受欢迎。也许很快它们将在各种任务中成为新的最先进技术，就像Transformer替代LSTM和CNN一样。但首先，让我们先看看Transformer。

本文并不是为了解释Transformer架构，因为已经有足够多的优秀文章对此进行了详尽的说明。本文的目的更多是从不同的角度来看待它，或是澄清一些你尚未完全理解的细节。

了解 Transformer 的资源

如果你想要更详细地了解 Transformer 架构，可以参考以下材料:

首先，官方论文。虽然作为初次学习的材料可能不是最佳选择，但它并不像看起来那么复杂。
Jay Alammar 的《Transformer 可视化解析》是一篇很棒的文章。如果你不喜欢阅读，可以观看同一作者的 YouTube 视频。
如果你想直接实践并使用各种 Transformer 模型来构建实际应用，可以参考 Hugging Face 的课程。

原始 Transformer

首先，让我们回顾一下 Transformer 的基本概念。

Transformer 的架构由两个部分组成：encoder（左侧）和decoder（右侧）。编码器接收一系列输入的 tokens，并生成一系列隐藏状态；解码器则接收这些隐藏状态，并生成一系列输出的 tokens。

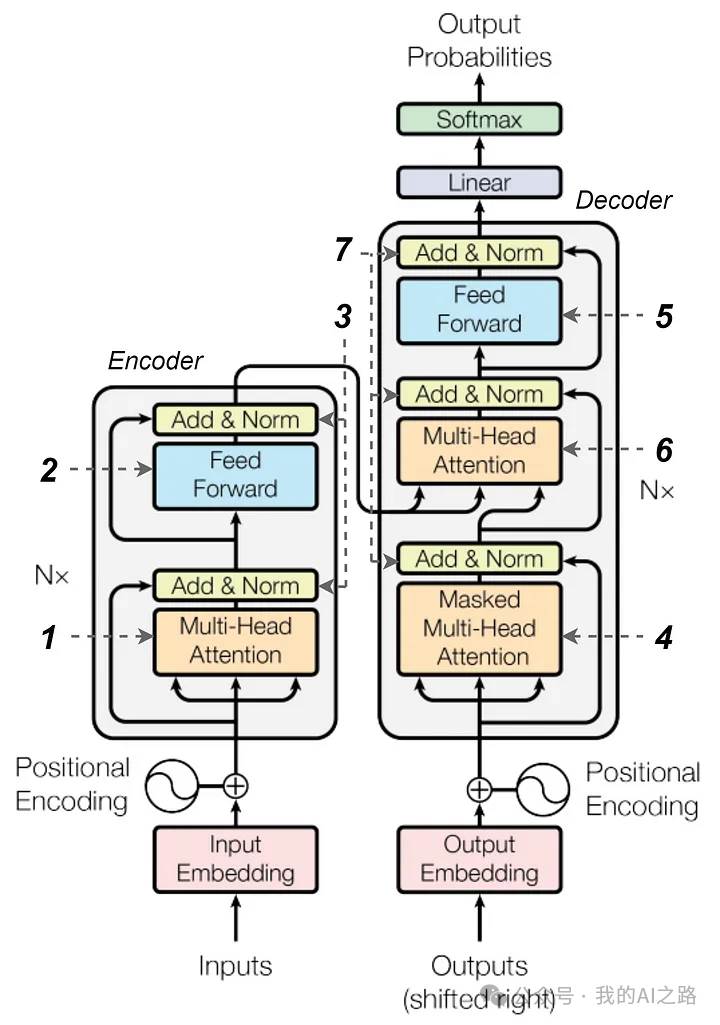
Encoder 和 Decoder 都由多层相同的结构堆叠而成。

对于Encoder，每一层包含两个主要部分：Multi-head Attention (1) 和 Feed-forward Neural Network (2)，并配有一些额外的结构，如 Layer Normalization (3) 和 Skip Connections。Multi-head Attention 能够并行处理不同的 attention heads，从而捕捉输入序列中的全局依赖关系，而 Feed-forward Neural Network 则对每个位置的输出进行进一步的处理。Layer Normalization 用于稳定和加速训练，而 Skip Connections 则帮助缓解梯度消失问题，保持信息流动。

Decoder的结构与 Encoder 相似，但除了包含第一个 Multi-head Attention (4)（在机器翻译任务中会被 masked，避免 Decoder 提前查看未来的 tokens）和Feed-forward Neural Network (5)之外，它还具有一个第二个 Multi-head Attention (6)，用于 Decoder 在生成输出时结合 Encoder 提供的上下文信息。通过这种机制，Decoder 可以灵活结合来自输入的全局信息进行输出生成。和 Encoder 一样，Decoder 也包含Layer Normalization (7) 和 Skip Connections，以确保训练过程中的稳定性与效率。

我在这里不会将输入的 Embedding Layer（包括 Positional Encoding）和最终的输出层（Linear + Softmax）视为 Transformer 的核心组件，而只专注于 Encoder 和 Decoder 块。因为这些组件（Embedding Layer 和输出层）是根据具体任务和 Embedding 方法定制的，而 Encoder 和 Decoder 堆栈则构成了许多其他架构的基础。

例如，以 BERT 为基础的架构主要使用 Encoder（如 BERT、RoBERTa、ALBERT、DeBERTa 等），而以 GPT 为基础的模型则主要依赖 Decoder（如 GPT、GPT-2、GPT-3、ChatGPT）。还有一些模型是基于完整的 Encoder-Decoder 框架构建的（如 T5、BART 等）。这些架构基于 Transformer 的 Encoder 和 Decoder 模块，但应用于不同的任务与领域。

虽然我们在这个架构中列出了七个组件，但实际上只有三个是独特的：

Multi-head Attention
Feed-forward Network
Layer Normalization

这些是 Transformer 架构的核心模块。无论是 Encoder 还是 Decoder，基本上都通过这三种组件以不同的方式进行组合，从而实现复杂的功能。其他部分，比如 Skip Connections 和 Masking，虽然重要，但主要是为了增强这三个核心模块的效果和适应不同的任务需求。

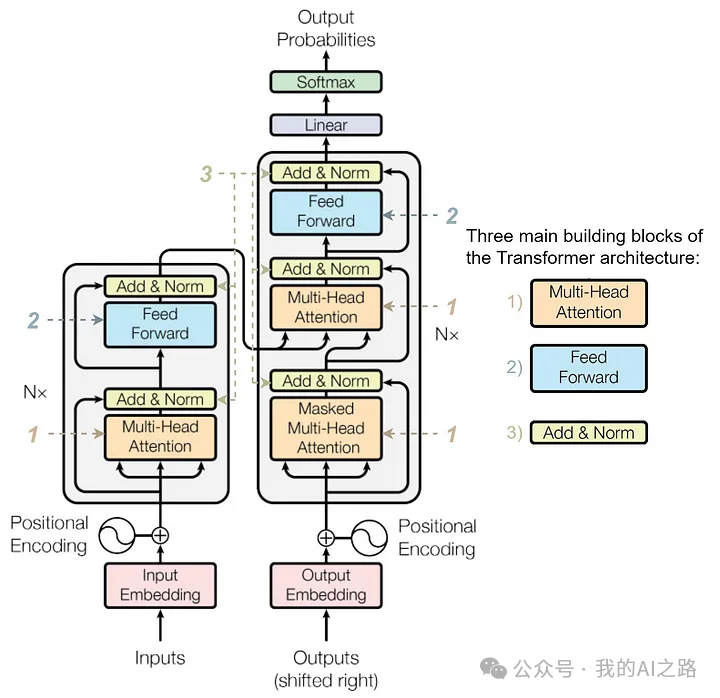
这些组件共同构成了 Transformer 的基础。让我们更详细地了解它们！

Transformer 的核心构建模块

接下来，我们将探讨每个模块的内部结构，并计算它们所需的参数数量。在这一部分中，我们还会开始使用 PyTorch 来验证我们的计算。

为了检查某个模型模块的参数数量，我将使用以下这行简单的代码函数：

import torch

# https://discuss.pytorch.org/t/how-do-i-check-the-number-of-parameters-of-a-model/4325/9
def count_parameters(model: torch.nn.Module) -> int:
""" 返回一个 PyTorch 模型中可学习参数的数量 """
# 对模型的所有参数进行遍历，只统计 requires_grad=True 的参数
# p.numel() 返回张量中的元素总数，也就是该参数的大小
return sum(p.numel() for p in model.parameters() if p.requires_grad)

这个函数可以帮助我们快速统计 PyTorch 模型中可训练参数的总数，并验证我们对各个模块参数数量的推测是否准确。在深入分析每个模块之前，确保了解这些基础计算非常有用。

在开始之前，请注意所有模块都是标准化的，并且都与 Skip Connections 一起使用。这意味着所有输入和输出的形状（更确切地说是它的最后一个维度，因为 batch size 和 tokens 数量可能会有所不同）必须保持一致。在原始论文中，这个维度（d_model）是 512。

Multi-Head Attention

著名的 Attention 机制是 Transformer 架构的核心。然而，抛开所有的动机和技术细节，Multi-Head Attention 实际上只是一些矩阵乘法的组合。

Multi-Head Attention 通过并行多个 attention heads 来捕捉输入中的不同信息，它允许模型从不同的角度处理序列中的关系。这种机制的优势在于它能够更好地捕捉长距离依赖关系，并且可以在不增加计算复杂度的前提下提升模型的表达能力。每个 attention head 的输出会被拼接在一起，随后通过一个线性变换层确保维度一致。

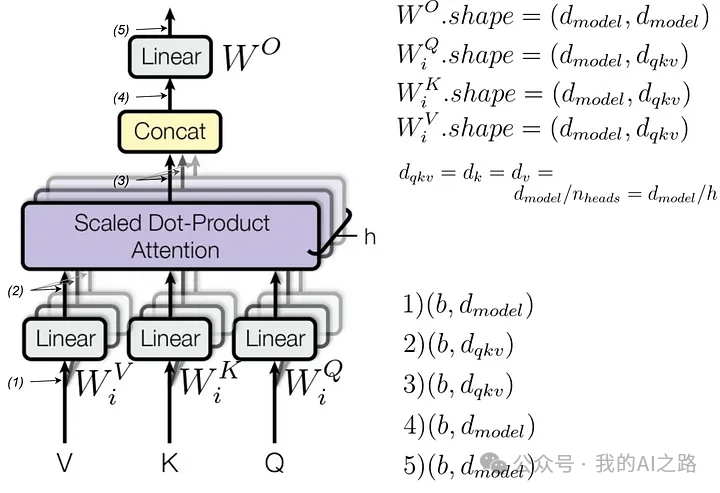
在为每个 head 计算完 Attention 之后，我们将所有的 heads 拼接在一起，并通过一个线性层（即 WO 矩阵）。每个 head 进行的是Scaled Dot-Product Attention，并且分别针对 query、key 和 value 进行了三次独立的矩阵乘法（对应的矩阵分别为 WQ,WK 和 WV）。这些矩阵对于每个 head 都是不同的，这也是为什么公式中带有下标 i。

最终的线性层 WO 的形状为dmodel X dmodel，而其余的三个矩阵WQ,WK 和WV 的形状相同，都是 dmodel X dqkv。

这些矩阵的作用是将输入向量分别映射到 query、key 和 value 空间中，随后通过 Scaled Dot-Product Attention 机制计算各个 tokens 之间的相关性，再将结果组合后通过线性变换以确保输出维度与输入一致。

在为每个 head 计算完 Attention 之后，我们将所有的 heads 拼接在一起，并通过一个线性层（即矩阵）。每个 head 进行的是Scaled Dot-Product Attention，并且分别针对 query、key 和 value 进行了三次独立的矩阵乘法（对应的矩阵分别为 , 和）。这些矩阵对于每个 head 都是不同的，这也是为什么公式中带有下标。最终的线性层的形状为，而其余的三个矩阵 , 和的形状相同，都是。

请注意，在上图中在原始论文中被表示为或。我选择使用这个名称，因为虽然这些矩阵的形状可能不同，但它们在计算中维度一致。另外需要注意的是，（在论文中用 h 表示）。因此，必须能够被 num_heads 整除，以确保后续拼接时形状正确。这种设计保证了每个 head 处理的维度相同，最终可以将多个 attention heads 的结果拼接在一起，而不会出现维度不匹配的问题。这也是 Transformer 架构能够并行处理不同注意力机制的关键所在。

你可以通过检查上图中各个中间阶段的形状来测试自己（正确的形状已在右下角标出）。

最终，我们为每个 head 需要三组较小的矩阵，以及一个较大的最终矩阵。那么，总共需要多少参数呢？（不要忘记还需要计算 bias 参数。）

矩阵的参数计算：这里的是拼接了多个 heads 的输出后通过的线性变换矩阵，它的参数量为：（线性层通常带有偏置参数，偏置的维度等于输出的维度。因此，偏置的参数数量是）。
、和的参数计算：每个 head 都有自己的 query、key 和 value 矩阵，其参数量为：由于有个 head，每个 head 需要 3 个这样的矩阵，因此总共的参数量为：。这个公式展示了 Multi-head Attention 中每个 head 的 query、key 和 value 矩阵的参数数量。

近似的参数数量之所以这样计算，是因为我们可以忽略与相比的影响。让我们使用 PyTorch 来验证这个结论。通常在大模型中，平方项（如）会比线性项（如）大得多。因此，在计算参数量时，可以忽略较小的线性项，这就是为什么近似参数数量可以简化为。接下来，我们可以使用 PyTorch 来检验这个公式是否正确。通过简单的代码，我们可以快速验证理论计算与实际的模型参数数量是否一致。

from torch import nn  # 导入 PyTorch 中的神经网络模块

# 设置模型的维度参数 d_model 和注意力头的数量 n_heads
d_model = 512  # d_model 表示 Transformer 中的特征维度
n_heads = 8  # n_heads 表示多头注意力中的 head 数量，必须能整除 d_model

# 定义一个 PyTorch 的多头注意力层，使用 nn.MultiheadAttention
# embed_dim 参数对应 d_model，num_heads 参数对应 n_heads
multi_head_attention = nn.MultiheadAttention(embed_dim=d_model, num_heads=n_heads)

# 使用之前定义的 count_parameters 函数计算多头注意力层的参数数量
# 这个函数会返回该层中所有可训练参数的总数量
print(count_parameters(multi_head_attention))  # 输出 1050624，即多头注意力机制的总参数量

# 理论上，我们可以使用公式 4 * (d_model * d_model + d_model) 计算参数数量
# 这个公式是根据我们之前的推导得到的近似参数数量，忽略了较小的线性项
print(4 * (d_model * d_model + d_model))  # 输出 1050624，验证公式计

数对的上，说明成功了。

针对所有自学遇到困难的同学们，我帮大家系统梳理大模型学习脉络，将这份 LLM大模型资料 分享出来：包括LLM大模型书籍、640套大模型行业报告、LLM大模型学习视频、LLM大模型学习路线、开源大模型学习教程等, 😝有需要的小伙伴，可以 扫描下方二维码领取🆓↓↓↓

👉[CSDN大礼包🎁：全网最全《LLM大模型入门+进阶学习资源包》免费分享（安全链接，放心点击）]()👈

Feed-forward Network

Transformer 中的 Feed-forward Network (FFN) 由两层全连接层组成，中间夹有一个 ReLU 激活函数。这个网络的设计使得其内部层（隐藏层）的表达能力比输入和输出更强大，而输入和输出的维度必须保持一致（正如我们之前提到的）。

一般情况下，FFN 的结构如下：

在原始论文中, 被设置为 2048，这意味着网络的隐藏层维度是输入/输出维度的 4 倍，从而增强了模型的表达能力。

具体解释：

第一层全连接层：从输入的维度映射到更高的内部维度，即。
ReLU 激活函数：在两层全连接层之间，使用 ReLU 来引入非线性。
第二层全连接层：将内部维度映射回原来的，即。

调整公式：

完整的公式可以表达为：

其中，是隐藏层的维度，是输入/输出的维度。

这种设计通过将输入维度暂时扩展到更高的维度，再缩回到原始维度，从而增加了网络的表达能力。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

一点可视化展示总是有帮助的。

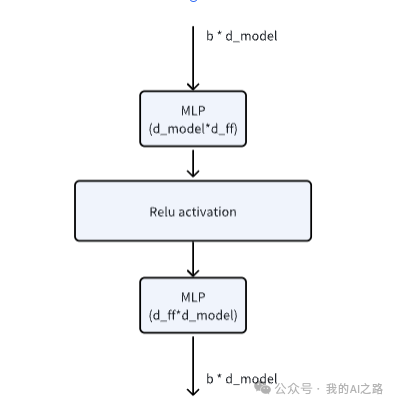
参数的计算相对简单，关键是不要被 biases（偏置）搞混。

我们可以通过以下代码描述这样一个简单的网络，并检查它的参数数量（请注意，PyTorch 的官方实现还使用了 Dropout，我们稍后会在 **Encoder/**Decoder 代码中看到这一点。但正如我们所知，Dropout 层没有可训练的参数，因此这里为了简化，我省略了它）：

在这个例子中，我们的重点是计算网络中的可训练参数，例如权重和偏置。而 Dropout 层的作用是为了防止过拟合，但它不涉及参数的更新，因此在参数计算中可以忽略。

from torch import nn  # 导入 PyTorch 中的神经网络模块

# 定义 Transformer 中的 Feed-forward Network 模块
class TransformerFeedForward(nn.Module):
def __init__(self, d_model, d_ff):
"""
        初始化函数，构造 Feed-forward Network 的结构
        参数:
        - d_model: Transformer 输入和输出的特征维度
        - d_ff: Feed-forward Network 中隐藏层的扩展维度（通常为 d_model 的四倍）
        """
super(TransformerFeedForward, self).__init__()
self.d_model = d_model  # 保存输入输出的特征维度
self.d_ff = d_ff  # 保存隐藏层的特征维度

# 定义第一层线性层 (MLP)，将输入维度从 d_model 扩展到 d_ff
self.linear1 = nn.Linear(self.d_model, self.d_ff)

# ReLU 激活函数，添加非线性
self.relu = nn.ReLU()

# 定义第二层线性层 (MLP)，将维度从 d_ff 压缩回 d_model
self.linear2 = nn.Linear(self.d_ff, self.d_model)

# 定义前向传播函数，x 是输入的张量
def forward(self, x):
# 通过第一层线性层，维度从 d_model 扩展到 d_ff
        x = self.linear1(x)

# 应用 ReLU 激活函数，添加非线性
        x = self.relu(x)

# 通过第二层线性层，维度从 d_ff 压缩回 d_model
        x = self.linear2(x)

# 返回输出
return x

# 设置 Transformer 的输入输出维度 d_model 和隐藏层扩展维度 d_ff
d_model = 512  # 输入和输出的特征维度
d_ff = 2048  # 隐藏层的特征维度（通常是 d_model 的 4 倍）

# 初始化一个 Feed-forward Network 实例
feed_forward = TransformerFeedForward(d_model, d_ff)

# 打印 Feed-forward Network 中可训练参数的总数量
print(count_parameters(feed_forward))  # 2099712

# 计算公式 2 * d_model * d_ff + d_model + d_ff，用来验证总参数数量
print(2 * d_model * d_ff + d_model + d_ff)  # 2099712

通过该公式计算出的结果也是 2099712，与 count_parameters 函数得到的结果一致。

Layer Normalization

Transformer 架构中的最后一个重要模块是 Layer Normalization。简而言之，它是一种可学习的归一化方法，通过引入缩放（scaling）和偏移（shift），可以显著提高训练过程的稳定性。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

这里的可训练参数是两个向量：和，每个向量的维度为。在 Layer Normalization 中，和分别用于缩放和偏移归一化后的输出结果。由于每个输入特征都有一个相应的缩放和偏移参数，因此和的维度与输入特征的维度相同。具体来说，Layer Normalization 的输出公式为：

其中：

和是第个特征对应的缩放和偏移参数，均为可学习的。
是归一化后的第个特征。因此，Layer Normalization 的总可训练参数数量为，因为每个输入特征有一个和一个参数。

总结：

和是 Layer Normalization 中的两个可学习参数，分别用于缩放和偏移。
每个输入维度都有相应的和参数，因此总的可训练参数数量为。

from torch import nn  # 导入 PyTorch 中的神经网络模块

# 设置 Transformer 中的特征维度 d_model
d_model = 512  # d_model 表示输入和输出的特征维度

# 定义一个 Layer Normalization 模块
# nn.LayerNorm 是 PyTorch 中实现 Layer Normalization 的类，它接受一个 d_model 维度
layer_normalization = nn.LayerNorm(d_model)

# 打印 Layer Normalization 中的可训练参数总数
# 这个函数会返回两个向量 gamma 和 beta 的参数数量，它们的维度都是 d_model
print(count_parameters(layer_normalization))  # 输出 1024

# 理论上，我们知道 Layer Normalization 有两个可学习的向量：gamma 和 beta
# 因此总参数量应该是 2 * d_model，即：
print(d_model * 2)  # 输出 1024

详细解释：

1.设置 d_model：

d_model = 512：表示输入特征的维度。在 Layer Normalization 中，每个输入维度都会有对应的可训练参数和。

2.创建 Layer Normalization 模块：

layer_normalization = nn.LayerNorm(d_model)：这是 PyTorch 中的 Layer Normalization 实现。它会根据给定的特征维度 d_model 初始化两个可训练的参数向量和，用于缩放和偏移归一化后的特征。

3.计算可训练参数：

count_parameters(layer_normalization)：使用之前定义的 count_parameters 函数，计算 Layer Normalization 模块中的可训练参数数量。因为我们有两个向量（和），每个向量的维度为 d_model，因此总参数数量为 512 * 2 = 1024。

4.理论验证：

print(d_model * 2)：这里直接手动计算参数数量。由于 Layer Normalization 包含两个可训练的向量和，每个向量的维度是 d_model，所以总参数量为 512 * 2 = 1024。Layer Normalization 的总参数量是，而 Feed-forward Network 和 Multi-head Attention Block 的参数量通常为的数量级。由于前者的参数量相对较小，即使 Layer Normalization 出现在模型的每一层，其对总参数量的贡献也很小。因此，在总参数计算时，Layer Normalization 的影响通常被忽略。

Encoder和Decoder

现在我们已经具备了计算整个 **Encoder/**Decoder 模块参数的所有基础！

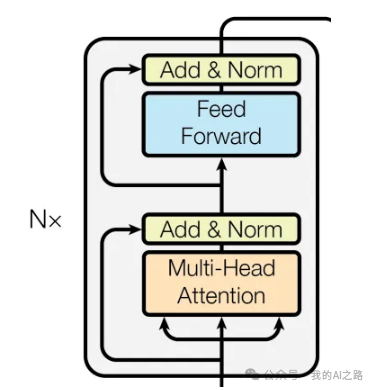
回顾一下，Encoder 由以下模块组成：

一个 Attention Block（注意力模块）
一个 Feed-forward Network（前馈神经网络）
两个 Layer Normalizations（层归一化）

Encoder 的参数计算：

1.Attention Block：

Multi-head Attention 的参数计算公式为：

其中，。

2.Feed-forward Network：

Feed-forward Network 的参数计算公式为：

3.Layer Normalization：

Layer Normalization 的参数量较小，仅为：

总参数公式：因此，一个 Encoder 的总参数量可以表示为：

完整公式为：

from torch import nn

# 创建一个 Transformer Encoder Layer，d_model 设置为 512，n_heads 设置为 8
encoder_layer = nn.TransformerEncoderLayer(d_model=512, nhead=8)

# 输出 encoder_layer 的内部结构
print(encoder_layer)

TransformerEncoderLayer(
  (self_attn): MultiheadAttention(
    (out_proj): NonDynamicallyQuantizableLinear(in_features=512, out_features=512, bias=True)
  )
  (linear1): Linear(in_features=512, out_features=2048, bias=True)
  (dropout): Dropout(p=0.1, inplace=False)
  (linear2): Linear(in_features=2048, out_features=512, bias=True)
  (norm1): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
  (norm2): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
  (dropout1): Dropout(p=0.1, inplace=False)
  (dropout2): Dropout(p=0.1, inplace=False)
)

正如上面提到的，这个实现中在 Feed-forward Network 中包含了 Dropout 层。现在我们也可以看到与 Layer Normalization 相关的 Dropout 层。

Decoder 由两个 Attention Blocks、一个 Feed-forward Network 和三个 Layer Normalizations 组成。

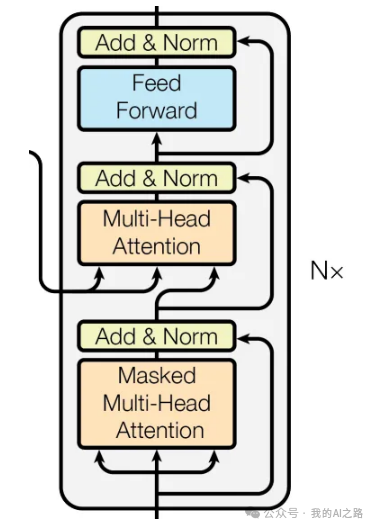
Decoder的结构：

两个 Attention Blocks：

第一个 Attention Block 处理目标序列自身的依赖关系，确保在生成序列时，不会看到未来的 token（通常通过 Masking 实现）。
第二个 Attention Block 从 Encoder 中获取上下文信息，结合编码器的输出进行进一步处理。

Feed-forward Network：

与 Encoder 中的 Feed-forward Network 相同，它包含两个全连接层以及 ReLU 激活函数，通常在两个 Attention Blocks 之后应用。

Layer Normalization：

Decoder 中有三个 Layer Normalizations：一个用于每个 Attention Block 之后，一个用于 Feed-forward Network 之后。每个 Layer Normalization 都有可学习的参数和，用于缩放和偏移归一化结果。

参数公式：

对于 Decoder，总参数量可以表示为：

具体公式为：

这个公式反映了 Decoder 各部分的总参数量，结合了 Multi-head Attention、Feed-forward Network 和 Layer Normalization 的参数贡献。

from torch import nn

# 创建一个 Transformer Decoder Layer，d_model 设置为 512，n_heads 设置为 8
decoder_layer = nn.TransformerDecoderLayer(d_model=512, nhead=8)

# 输出 decoder_layer 的内部结构
print(decoder_layer)

TransformerDecoderLayer(
  (self_attn): MultiheadAttention(
    (out_proj): NonDynamicallyQuantizableLinear(in_features=512, out_features=512, bias=True)
  )
  (multihead_attn): MultiheadAttention(
    (out_proj): NonDynamicallyQuantizableLinear(in_features=512, out_features=512, bias=True)
  )
  (linear1): Linear(in_features=512, out_features=2048, bias=True)
  (dropout): Dropout(p=0.1, inplace=False)
  (linear2): Linear(in_features=2048, out_features=512, bias=True)
  (norm1): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
  (norm2): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
  (norm3): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
  (dropout1): Dropout(p=0.1, inplace=False)
  (dropout2): Dropout(p=0.1, inplace=False)
  (dropout3): Dropout(p=0.1, inplace=False)
)

最终公式

在确认无误后，我们可以编写以下函数来计算参数的数量。事实上，这个函数只需要三行代码，甚至可以合并为一行。其余的部分是用来进行解释的 docstring。

def transformer_count_params(d_model=512, d_ff=2048, encoder=True, approx=False):
"""
    计算 Transformer Encoder/Decoder 的参数数量。

    参数计算公式如下：
        - multi-head attention（多头注意力模块）: 
          4*(d_model^2 + d_model) 如果 approx=False,
          否则为 4*d_model^2。
        - feed-forward（前馈网络）:
          2*d_model*d_ff + d_model + d_ff 如果 approx=False,
          否则为 2*d_model*d_ff。
        - layer normalization（层归一化）:
          2*d_model 如果 approx=False,
          否则为 0（忽略 Layer Normalization 的参数量）。

    **Encoder 模块**包括：
        1 个 multi-head attention 模块，
        1 个 feed-forward 网络，
        2 个 layer normalizations。

    **Decoder 模块**包括：
        2 个 multi-head attention 模块，
        1 个 feed-forward 网络，
        3 个 layer normalizations。

    参数：
    - d_model: (int) 模型的特征维度，即输入和输出向量的维度。
    - d_ff: (int) 前馈网络的隐藏层维度，通常是 d_model 的 4 倍。
    - encoder: (bool) 如果为 True，返回 Encoder 的参数数量，否则返回 Decoder 的参数数量。
    - approx: (bool) 如果为 True，返回近似的参数数量（忽略较小的项），否则返回精确结果。

    返回：
    - (int) Transformer Encoder/Decoder 中可训练的参数数量。
    """

# 计算 multi-head attention 的参数数量
# 如果 approx=True，则忽略较小的线性项，只计算近似的 d_model^2 项
    attention = 4 * (d_model ** 2 + d_model) if not approx else 4 * d_model ** 2

# 计算前馈网络的参数数量
# 如果 approx=True，则忽略偏置部分，简化为 2 * d_model * d_ff
    feed_forward = 2 * d_model * d_ff + d_model + d_ff if not approx else 2 * d_model * d_ff

# 计算 layer normalization 的参数数量
# 如果 approx=True，则忽略 Layer Normalization 的参数量，设置为 0
    layer_norm = 2 * d_model if not approx else 0

# 如果是 Encoder：
# 1 个 multi-head attention + 1 个 feed-forward + 2 个 layer normalization
if encoder:
return attention + feed_forward + 2 * layer_norm
# 如果是 Decoder：
# 2 个 multi-head attention + 1 个 feed-forward + 3 个 layer normalization
else:
return 2 * attention + feed_forward + 3 * layer_norm

现在，我们去测试他是否正确：

from torch import nn  # 导入 PyTorch 中的神经网络模块

# 创建一个 Transformer Encoder Layer，d_model 设置为 512，n_heads 设置为 8
encoder_layer = nn.TransformerEncoderLayer(d_model=512, nhead=8)

# 使用 count_parameters 函数计算 encoder_layer 的参数数量
# 打印结果为 3152384，即 Encoder 中的可训练参数总数
print(count_parameters(encoder_layer))  # 输出 3152384

# 使用 transformer_count_params 函数精确计算 Encoder 的参数数量，设置 approx=False 表示不使用近似计算
# 结果应与 count_parameters 函数一致，为 3152384
print(transformer_count_params(d_model=512, d_ff=2048, encoder=True, approx=False))  # 输出 3152384

# 使用 transformer_count_params 函数进行近似计算，设置 approx=True
# 由于忽略了较小的线性项，近似结果为 3145728，与精确结果有约 0.21% 的差异
print(transformer_count_params(d_model=512, d_ff=2048, encoder=True, approx=True))   # 输出 3145728

# 近似计算与精确计算之间的差异为约 0.21%

# 创建一个 Transformer Decoder Layer，d_model 设置为 512，n_heads 设置为 8
decoder_layer = nn.TransformerDecoderLayer(d_model=512, nhead=8)

# 使用 count_parameters 函数计算 decoder_layer 的参数数量
# 打印结果为 4204032，即 Decoder 中的可训练参数总数
print(count_parameters(decoder_layer))  # 输出 4204032

# 使用 transformer_count_params 函数精确计算 Decoder 的参数数量，设置 approx=False 表示不使用近似计算
# 结果应与 count_parameters 函数一致，为 4204032
print(transformer_count_params(d_model=512, d_ff=2048, encoder=False, approx=False))  # 输出 4204032

# 使用 transformer_count_params 函数进行近似计算，设置 approx=True
# 由于忽略了较小的线性项，近似结果为 4194304，与精确结果有约 0.23% 的差异
print(transformer_count_params(d_model=512, d_ff=2048, encoder=False, approx=True))   # 输出 4194304

# 近似计算与精确计算之间的差异为约 0.23%