更多的更多可以关注we chat公众号:AI wans 我们不见不散
世界坐标系:
🧭 世界坐标系,这是我们平时最常使用的坐标系(笛卡尔坐标系),比如数学里的(x,y)、(x,y,z)。
-
在2D中,一个点是(x,y)
-
在3D中,一个点是(x,y,z)
坐标是没有任何限制的,可能是(100,200,-50),也可能是(0.5,1.2,1.3)
坐标轴的单位一般是真实的物理单位,小到微米,大到光年,或者其他各种各样的虚拟单位。
在计算机图形学中,我们将最初建模、设置物体位置的空间就叫做
✅ 世界坐标系
例如:在3D游戏中建了一个小房子,其中一堵墙的位置是(10,0,-5)
世界坐标系用来描述"场景中物体的 绝对位置"
观察视角:
👁观察视角,从世界坐标到相机坐标
你不会直接看到世界坐标系的所有内容,而是用相机观察它。
所以我们会自然而然地有新的
✅ 相机坐标系
-
世界坐标变换到以相机为原点的坐标系
-
如果你把相机放在(0,0,0),朝向z轴负方向,那么所有场景都要"反向变换"过来
-
得到的点仍然是世界坐标(笛卡尔坐标系),例如(3,4,-10)
投影变换&NDC空间:
🪟投影变换,把三维世界映射到二维平面
真实世界是三维的,但我们的显示器等显示设备都是二维的(包括我们看到的也都是二维图像)。
我们通过投影变换矩阵(如透视投影、正交投影)把3D点映射到一个叫
✅ 裁剪空间(Clip Space)
我们着重了解一下这个变换的过程:
1.问题背景:从3D到2D
我们生活在3D世界,点有(x,y,z)坐标;
但屏幕是2D平面,像素只有(x,y)
✨目标:
如何把3D世界里的点,投影到2D平面上,同时保留近大远小的透视感呢?
2.齐次坐标&齐次变换
在图形学中,我们将3D点(x,y,z)表示为四维齐次坐标(x,y,z,1)
这是为了方便用4*4的投影矩阵来统一处理所有的线性变换(旋转、平移、缩放、透视、投影等)
这里我们补了一个 ... 1?
接下来,我们针对这个“1”做一下具体解析:
一.齐次坐标的本质:用高维空间描述低维空间
齐次坐标通过在n维空间中增加一个维度(即第n+1维),将低维空间的点、向量或变换用线性代数统一表示。对于3D而言,四维齐次坐标(x,y,z,w)中:
-
当w=1时,表示标准3D空间中的点(x,y,z)
-
当w=0时,表示3D空间中的向量(方向)
二.“1”的核心作用:统一变换矩阵运算
在图形学中,模型变换、视图变换、投影变换等均通过矩阵乘法实现。若直接用 3D 坐标 (x, y, z),平移变换需要非线性运算(加法),而旋转、缩放是线性运算(矩阵乘法),这导致变换无法统一表示。
引入齐次坐标后:
1.平移变换可表示为矩阵乘法
例如空间中一点沿x轴平移t的变换矩阵为:

这样坐标为(x,y,z,1)的点,变换后得到的结果是(x+t,y,z,1),等价于三维空间的平移
具体的数学表达为
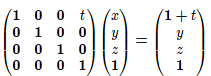
2.线性变换(旋转、缩放)与平移可以统一为4*4矩阵运算
缩放变换矩阵:
具体的使用就是
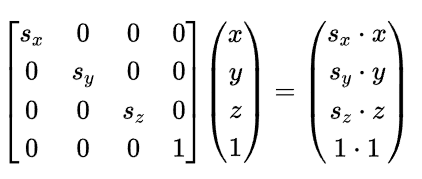
可以看出 s_x,s_y,s_z即为三个方向上的缩放因子
旋转矩阵
例如:

就是一个典型的旋转矩阵
这个是沿着z轴旋转θ角
(一个简单的技巧是从上到下分别为x,y,z,哪一行关于角度的函数即关于哪个轴旋转)
这样通过将点的齐次坐标与旋转矩阵相乘,可以实现点的旋转操作!
综上,通过加了这么一个“1”,我们大大的简化了图形学管线的数学逻辑。
3&4.投影矩阵&从相机空间到裁剪空间
🧮透视变换的核心就在于投影矩阵(以OpenGL为例)
我们常用的透视投影的矩阵,会将相机空间中的点变换为裁剪空间中的4D向量 ![]()
OpenGL中常见的透视投影矩阵为P如下:
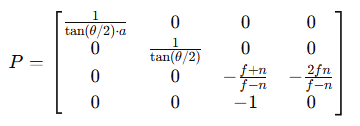
其中:
-
θ:视野角(FOV , Field of View)
-
a: 宽高比(aspect ratio = width/height)
-
n,f:近裁剪面、远裁剪面(near,far)
输出是裁剪空间四维向量:
![]()
接下来我们解释每一项的含义:
第一行(X投影):
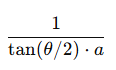
-
控制水平视角
-
比例因子保证 X 投影后被限制在 [−1,1][-1, 1][−1,1]
-
tan(θ/2) 表示相机的可视宽度角
第二行(Y投影):
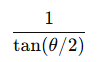
-
控制垂直视角
-
保证 y 值也被映射到 [−1,1]
第三行(Z轴非线性映射)
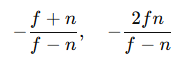
-
把 z 从相机空间中的 [n,f][n, f][n,f] 映射到 NDC 的 [−1,1]
-
映射是非线性的(透视深度不是线性分布)
-
保留深度缓存效果(近处更精细)
第四行(关键!:引入透视)
![]()
这是透视投影的核心:
- 它导致裁剪空间的 w 分量等于 −z
- 后续执行 齐次除法:
-
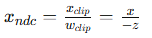
- 从而实现了“z 越小,屏幕上越大”的透视缩放效果!
从相机空间到裁剪空间:
假设相机空间中的一个点是:
![]()
那么通过投影矩阵后,得到:
![]()
但是这时候的x_clip,y_clip,z_clip并不是我们最重要用的值,必须做一次齐次除法:除以w
使用这个矩阵:
我们给定点:
![]()
经过矩阵乘法:
![]()
执行透视除法:
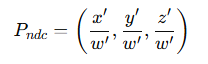
此时就成功进入了标准立方体范围,我们也就成功完成了缩放的工作,同时也成功进入了NDC空间。
NDC空间的意义就在于:
-
把来自各种世界的模型、坐标、大小,全都标准化到 [-1, 1] 范围
-
方便进行裁剪(比如 z > 1 的就太远了,不画了)
-
准备映射到屏幕(像素空间)
5.示例:
我们假设有一个点在世界坐标中就是:(100,50,-200)
我们要
-
用视图矩阵把它变成相机坐标系;
-
用投影矩阵变成裁剪坐标(x,y,z);
-
齐次除法得到NDC;
即为(0.5,-0.7,0.3)
这说明它:
-
x 在画面中心偏右
-
y 在画面中心偏下
-
z 距离在中等深度
最终映射到屏幕上,需要重新映射到实际像素空间,比如:
x_screen = (x_ndc + 1) * screen_width / 2
y_screen = (1 - y_ndc) * screen_height / 2 # 注意 y 方向一般反转
以上是我关于NDC的一些理解。







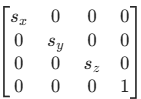
















 530
530

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








