电机控制进阶——PID速度控制_电机 pid 算法

位置式PID

位置式PID是当前系统的实际位置，与想要达到的预期位置的偏差，进行PID控制

• 比例P：e(k) 此次误差
• 积分I：∑e(i) 误差的累加
• 微分D：e(k) - e(k-1) 此次误差-上次误差

因为有误差积分 ∑e(i)，一直累加，也就是当前的输出u(k)与过去的所有状态都有关系。

位置式PID算法的伪代码如下：

//位置式PID（伪代码）
previous_err = 0;
integral = 0;
loop: //根据目标值与测量值(如电机的设定速度与读到的编码器转后后的速度)，循环计算更新输出值（如PWM）
	error = setpoint - measured_value;          /\*误差项：目标值-测量值\*/
	integral += error \* dt;                     /\*积分项：误差项的累计\*/
    derivative = (error - previous_error) / dt; /\*微分项：误差的变化率\*/
	output = Kp\*error + Ki\*integral + Kd\*derivative; /\*三项分别乘以PID系数即为输出\*/
	previous_err = err; //更新误差
	wait(dt); //等待固定的计算周期
	goto loop;

增量式PID

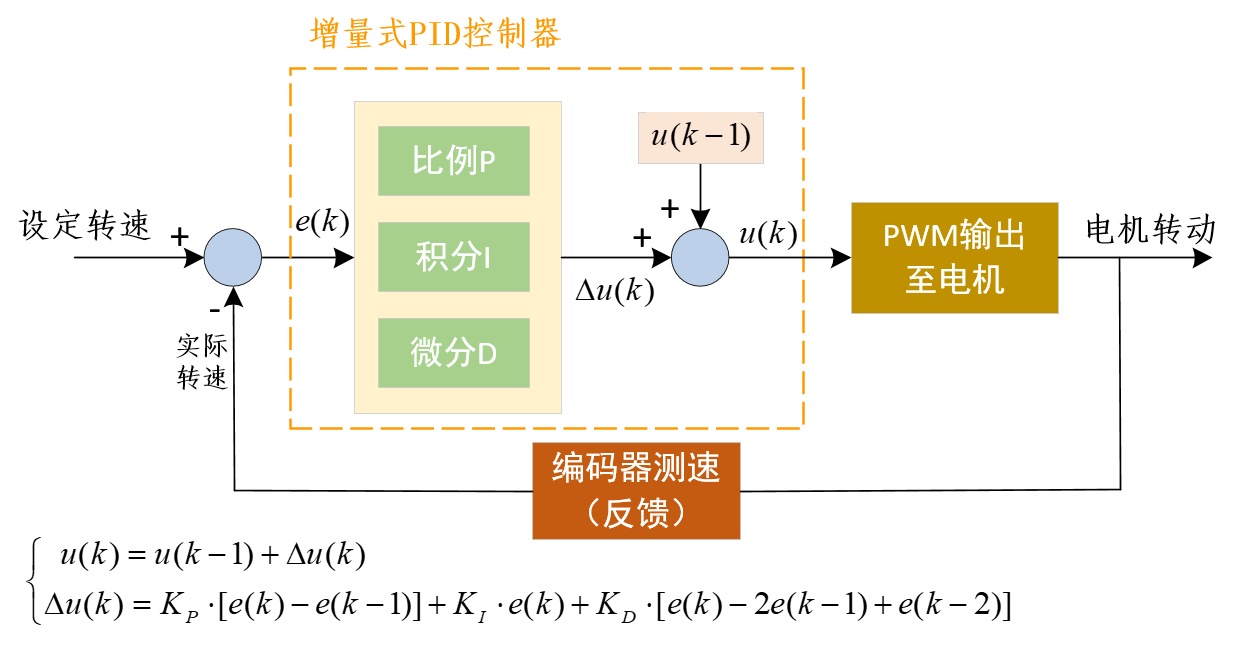
• 比例P：e(k) - e(k-1) 此次误差-上次误差
• 积分I：e(k) 此次误差d
• 微分D：e(k) - 2e(k-1)+e(k-2) 这次误差-2×上次误差+上上次误差

注意增量式PID首先计算的是Δu(k)，然后与上次的输出相加，才是此次的输出结果。增量式PID没有误差累加，控制增量Δu(k)的确定仅与最近3次的采样值有关。

增量式PID算法的伪代码如下：

//增量式PID（伪代码）
previous02_error = 0; //上上次偏差
previous01_error = 0; //上次偏差
integral = 0; //积分和
pid_out = 0; //pid增量累加和
loop:
    error = setpoint − measured_value;  /\*误差项：目标值-测量值\*/
    proportion = error - previous01_error;                            /\*比例项：误差项-上次偏差\*/
    integral = error \* dt;                                            /\*积分项：误差项的累计\*/
    derivative = (error − 2\*previous01_error + previous02_error) / dt;/\*微分项：上次误差与上上次误差的变化率\*/
    /\*或写成：derivative = ( (error − previous01\_error)/dt - (previous01\_error - previous02\_error)/dt )\*/
    pid_delta = Kp × error + Ki × integral + Kd × derivative; //计算得到PID增量
    pid_out = pid_out + pid_delta; //计算最终的PID输出

    previous02_error = previous01_error; //更新上上次偏差
    previous01_error = error; //更新上次偏差
    wait(dt); //等待固定的计算周期
    goto loop;

PID各项的作用

以这个弹簧为例（假设没有重力，只有空气阻力），先是在平衡位置上(目标位置)，拉它一下，然后松手，这时它会震荡起来。

P 比例

P就是比例的意思。这里就类比弹簧的弹力（回复力）：F=k*Δx

• 当物块距离平衡位置越远时，弹力越大，反之，离平衡位置越近，力越小。
• 当物块位于平衡位置上方时，弹性向下，当物块位于平衡位置下方时，弹性向上，即弹力总是使物块朝平衡位置施力。

D 微分/求导/变化率

只有P控制，物块一直在上下震荡，整个系统不是特别稳定。

这是因为空气阻力太小，想象一下整个把它放到水里，物块应该很快会静止下来。这时因为阻力的作用。

D的作用就相当于阻力：

• 它与变化速度（单位时间内的变化量）有关，变化的越大，它施加的阻力也就越大
• 它的方向与目标值无关，比如，当物块从下到上经过平衡位置时，它的方向一直是朝下，

即先是阻止物块靠近平衡位置，再是阻止物块远离平衡位置（对比P的作用，始终阻止物块远离平衡位置）

• 它的作用就是减小系统的超调量了（减少系统在平衡位置震荡）

I 积分/误差累积

有了P的动力和D的阻力，这个物块就可以较快的稳定下来了，那I的作用是什么呢？

想象一下，如果有其它外力的影响，在某一时刻，物块将要到达平衡位置时，恰好P的动力与外力(与P的作用方向相反的恒定力)抵消，则之后物块将停在此处附近（因为此时D的力也趋近0，并很快变为0），一直到达不了平衡位置。

这时，I的误差积分作用就很有必要了：

• 它计算的误差的累计，只要有误差，它就一直增加，开始可能很小，但只要没要到达平衡位置，该值就会越来越大
• 它的作用就是消除系统的静态误差了

PID参数整定

实际应用，进行PID参数调节时，一般使用试凑法，PID参数整定口诀如下：

参数整定找最佳，从小到大顺序查，

先是比例后积分，最后再把微分加，

曲线振荡很频繁，比例度盘要放大，

曲线漂浮绕大湾，比例度盘往小扳，

曲线偏离回复慢，积分时间往下降，

曲线波动周期长，积分时间再加长，

曲线振荡频率快，先把微分降下来，

动差大来波动慢，微分时间应加长，

理想曲线两个波，前高后低4比1，

一看二调多分析，调节质量不会低。

电机PID速度控制

上面介绍了PID的基础知识，接下来就使用位置式PID来实现对直流电机转速的控制。

程序

自定义PID结构体

typedef struct
{
	float target_val;   //目标值
	float err;          //偏差值
	float err_last;     //上一个偏差值
	float Kp,Ki,Kd;     //比例、积分、微分系数
	float integral;     //积分值
	float output_val;   //输出值
}PID;

PID算法实现(位置式PID)

float PID\_realize(float actual_val)
{
	/\*计算目标值与实际值的误差\*/
	pid.err = pid.target_val - actual_val;
	
	/\*积分项\*/
	pid.integral += pid.err;

	/\*PID算法实现\*/
	pid.output_val = pid.Kp \* pid.err + 
				     pid.Ki \* pid.integral + 
				     pid.Kd \* (pid.err - pid.err_last);

	/\*误差传递\*/
	pid.err_last = pid.err;

	/\*返回当前实际值\*/
	return pid.output_val;
}

周期调用PID计算

//周期定时器的回调函数
void AutoReloadCallback()
{
	int sum = 0;/\*编码器值（PID输入）\*/
	int res_pwm = 0;/\*PWM值（PID输出）\*/
	
    /\*读取编码器测量的速度值\*/
	sum = read\_encoder();
    /\*进行PID运算，得到PWM输出值\*/
    res_pwm = PID\_realize(sum);
	/\*根据PWM值控制电机转动\*/
	set\_motor\_rotate(res_pwm);
	
    /\*给上位机通道1发送实际值\*/
	set\_computer\_value(SEND_FACT_CMD, CURVES_CH1, &sum, 1); 
}

上位机

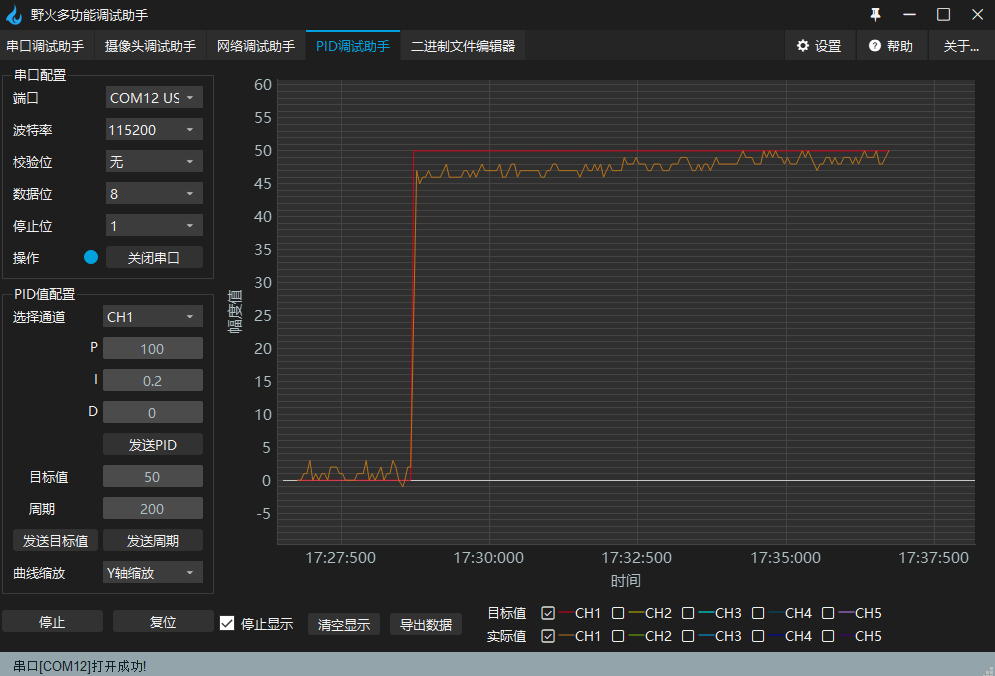
这里使用野火多功能调试助手的"PID调试助手“来进行实验，用于显示PID调节时的电机转速曲线。

实验演示

目标速度值设为50（这里的目标值50使用的是编码器10ms捕获的脉冲数），通过体调节PID的参数，来测试电机能否较快的达到目标速度。

先调节P

P值先使用10看看效果，从速度曲线可以看出，达不到目标速度，且与目标速度相差较大。

P	I	D
10	0	0

P值加大到100，从速度曲线可以看出，还是达不到目标速度。

P	I	D
100	0	0

只使用P，会存在静差，始终达到不了目标值，这时就要使用积分项来消除静差了。

再调节I

P保持100，I使用0.2，从速度曲线可以看出，可以达到目标速度，但跟随的速度较慢。

P	I	D
100	0.2	0

P保持100，加大I，使用1.0，从速度曲线可以看出，可以达到目标速度，跟随的速度加快了。

P	I	D
100	1.0	0

P保持100，继续加大I，使用3.0，从速度曲线可以看出，可以达到目标速度，跟随的速度进一步加快了。

P	I	D
100	3.0	0

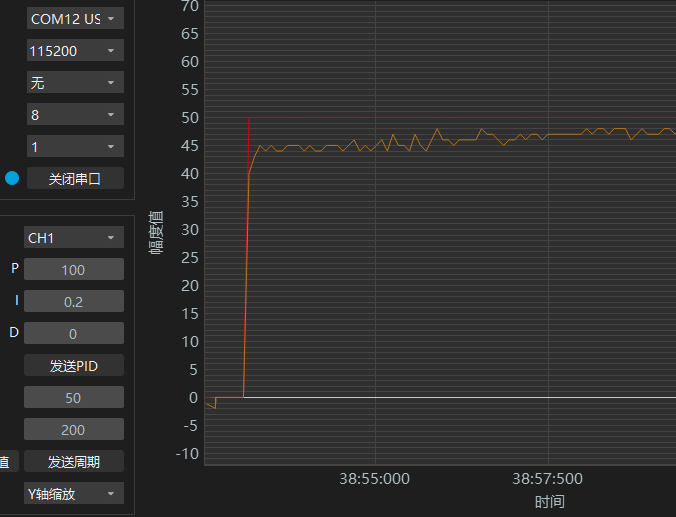
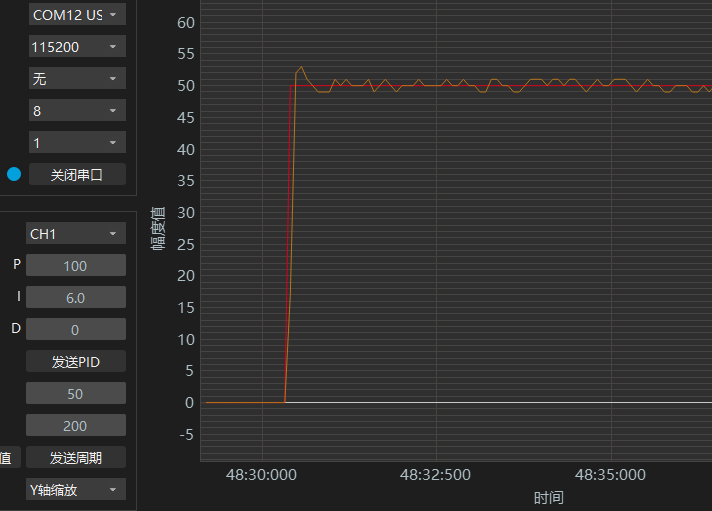
P保持100，再继续加大I，使用6.0，从速度曲线可以看出，可以达到目标速度，跟随速度也很快，但有一点过冲。

P	I	D
100	6.0	0