CSP 梦境巡查

目录

1.CSP 36

题目描述

思路

完整代码如下：

---

 

1.CSP 36

题目描述

梦境中的西西艾弗岛由 n+1n+1 个区域组成。梦境巡查员顿顿每天都会从梦之源（00 号区域）出发，顺次巡查 1,2,⋯,n1,2,⋯,n 号区域，最后从 nn 号区域返回梦之源。

在梦境中穿梭需要消耗美梦能量：

• 从梦之源出发时，顿顿会携带若干初始能量；

• 从第 ii 号区域前往下一区域（0≤i≤n0≤i≤n）需要消耗 aiai 单位能量，因此从第 ii 号区域出发时，顿顿剩余的美梦能量需要大于或等于 aiai 单位；

• 顺利到达第 ii 号区域（1≤i≤n1≤i≤n）后，顿顿可以从当地居民的美梦中汲取 bibi 单位能量作为补给。

假设顿顿初始携带 ww 单位美梦能量，那么首先需要保证 w≥a0w≥a0，这样顿顿便可消耗 a0a0 能量穿梭到 11 号区域、进而获得 b1b1 单位能量补给。巡查 11 号区域后，顿顿剩余能量为 w−a0+b1w−a0+b1，如果该数值大于或等于 a1a1，顿顿便可继续前往 22 号区域。依此类推，直至最后消耗 anan 单位能量从 nn 号区域返回梦之源，便算是顺利完成整个巡查。西西艾弗岛，又迎来安宁的一夜，可喜可贺！

思路

对于题背景不过多描述，主要是处理思路

首先放在最前面的是我意识到自己做题的一个机试题的一个毛病：特别爱凑

具体表现在：遇到输出不一致的情况，不爱推导，爱修改边边角角，希望凑出样例答案！ 我觉得这是一个非常不好的习惯，严重影响完成题目的时间。

我认为应该的做题思路是：

1. 根据题目进行一个理论分析，找到最简单且可行的办法

2. 尝试进行推导，确实可行后，先不写代码

3. 尝试优化，感觉可行

4. 详细推导，证明可行

5. 使用样例进行从输入到输出的推导

6. 最后根据推导写代码

理由是：

1. 写代码，写着写着容易忘记自己的思路是什么，所以先把思路记录下来

2. 理论的演算，相较于代码验证，跟容易判断正确性，以及节省时间

其他的不说了，正式进入题目分析：

首先：如果采用模拟的话，本题思路比较简单，但是复杂度过不去，O（n2）

所以我们需要进行优化：

通过w0,w1,w2...的推导，我们发现

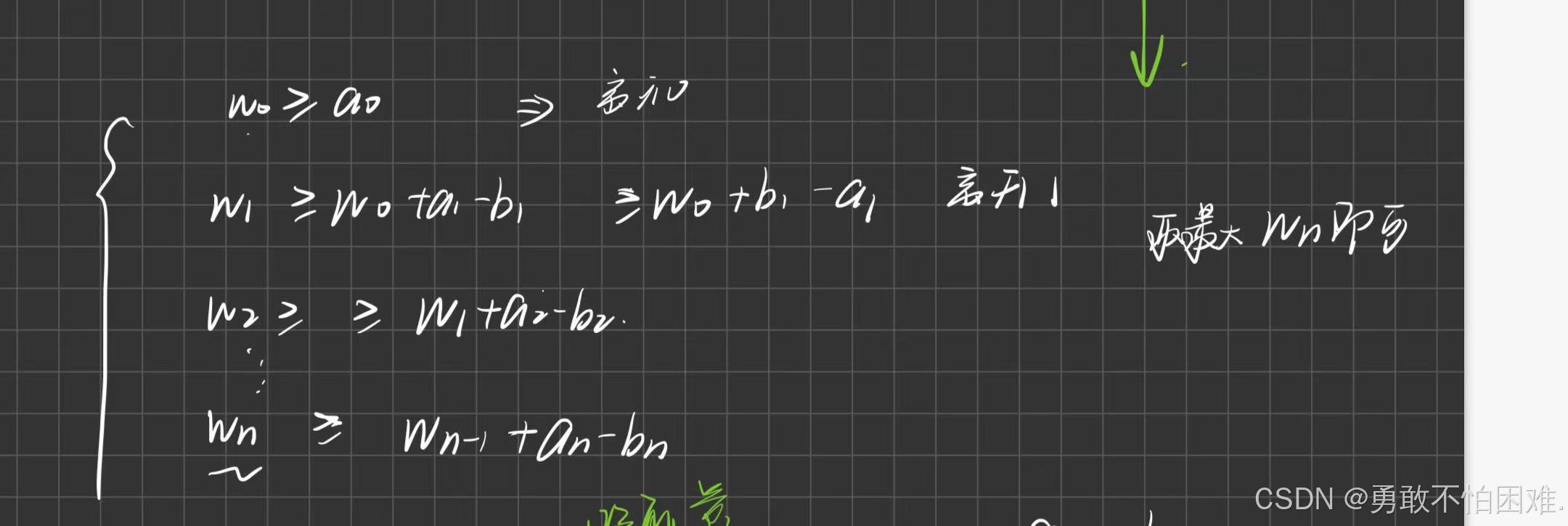
存在这样的关系，就是我如果要能够离开n点，那么我携带的能量wn，要满足离开第n个点的条件（废话！）。

我们从点0开始递推：

如果要离开第0个点，拿我携带的能量必须大于a0

如果要能够离开第1个点，那我携带的能量必须先支持我离开0点(w0)，然后的余下的能量够我离开1点（a1-b1）.

如果要能够离开第2个点，那我携带的能量必须先支持我离开1点(w1)，然后余下的能量够我离开2点（a2-b2）。

所以递推到n就能获得要能够离开第n个点，所需要的能量

所以为了能离开这里面的n个点，我需要选择（w0,w1,...,wn）里面最大的能量，这样就确保，在每一个点都能够离开

以上是不考虑没有能量的情况

所以引入损失能量的情况，

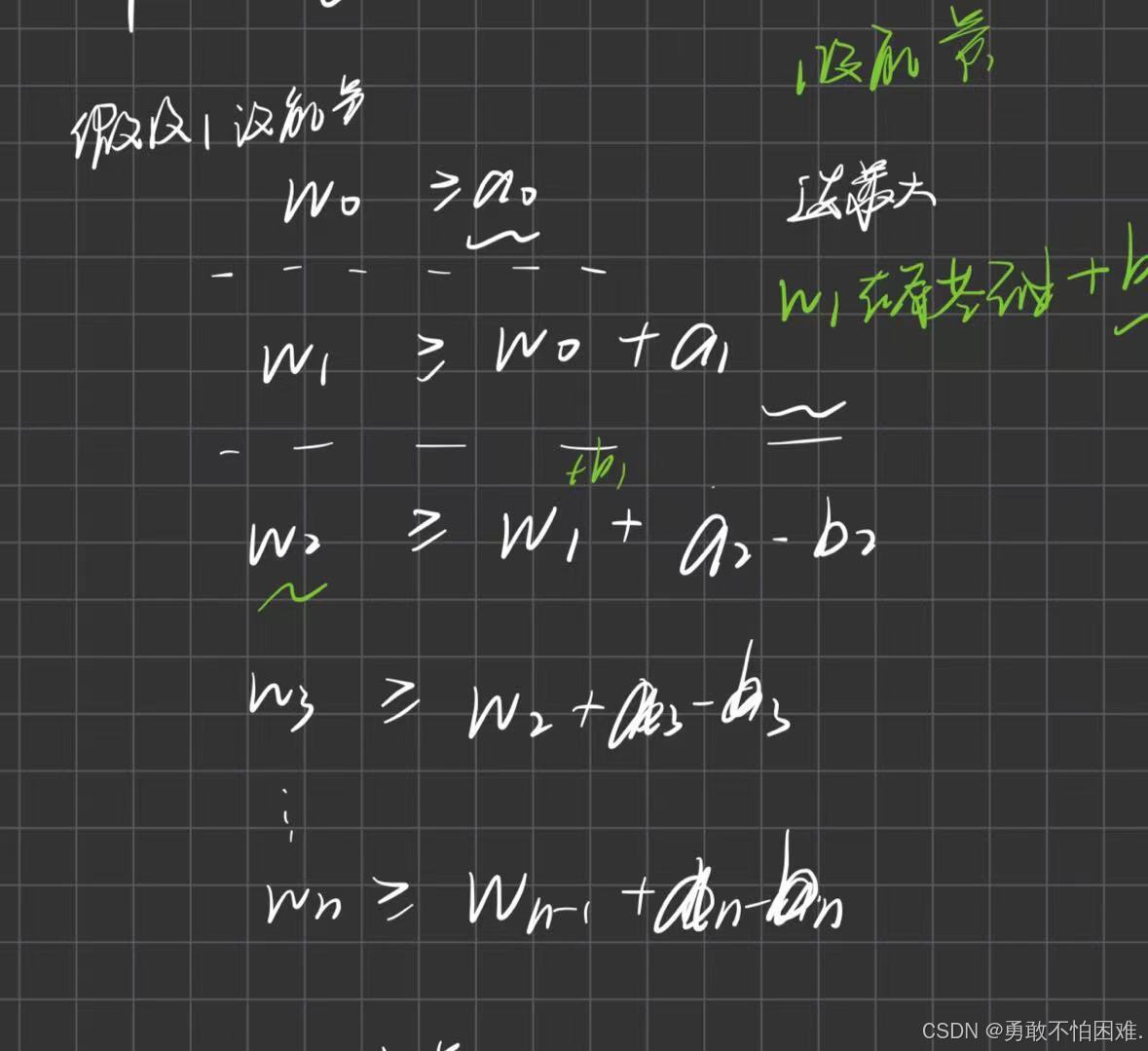
这里假设1的能量没了

所以对于原来的不等式而言，就是在w1这里发生了改变，我在这个位置需要的能量多了，但于此同时，我第1个位置需要的能量多了，后面所需要的能量也就多了相同的一些。

所以这个时候所需要最大的能量就是：a. 保证能够到达1点的能量 b.保能够离开1点的能量 ,a,两个能量取最大即可

同理，对于第i个位置的能量没了,就是要保证

a. 保证能够到达i点的能量

b.保能够离开i点的能量 ,

a,b两个能量取最大即可

这里我们把这两种情况进行一个对比：

对于不损失能量的(w0,w1,...,wn)和损失1的能量（w0,w1...wn）而言

后面的w1会比前面的w1大一个b1 同理w2和w3...wn都是同样的大了一个b1

所以最后的结论就是：

如果第i个位置的能量损失了，

对于前面的w0,w1...,wi-1都不受影响，找最大的就完事了

对于后面的wi,wi+1...,wn都会相同的放大bi

所以我要的答案就是左右两边的最大值，再取一个最大值

所以我们把完全不受影响的(w0,w1...,wn)计算出来

w=[0 for i in range (n+1)]
w[0]=a[0]
for i in range(1,n+1):
    w[i]=w[i-1]+a[i]-b[i]

也就这张图的内容（不损失能量的情况）

然后在记录一下0到i-1中最大的

和i到n中最大的数

prefix=[0 for i in range (n+1)]
suffix=[0 for i in range (n+1)]
for i in range(1,n+1):
    prefix[i]=max(prefix[i-1],w[i-1])
suffix[n]=w[n]
for i in range (n-1,0,-1):
    suffix[i]=max(suffix[i+1],w[i])

最后答案如下：

第1个就是1左边的最大的，和1右边最大的+b[1]即可

res=[0 for i in range (n+1)]
for i in range(1,n+1):
    res[i]=max(prefix[i],suffix[i]+b[i])
res_last=res[1:]

完整代码如下：
 

import copy

n=int(input())
a=list(map(int,input().split()))
b=[0]
c=list(map(int,input().split()))
b=b+c

w=[0 for i in range (n+1)]
w[0]=a[0]
for i in range(1,n+1):
    w[i]=w[i-1]+a[i]-b[i]
prefix=[0 for i in range (n+1)]
suffix=[0 for i in range (n+1)]
for i in range(1,n+1):
    prefix[i]=max(prefix[i-1],w[i-1])
suffix[n]=w[n]
for i in range (n-1,0,-1):
    suffix[i]=max(suffix[i+1],w[i])

res=[0 for i in range (n+1)]
for i in range(1,n+1):
    res[i]=max(prefix[i],suffix[i]+b[i])
res_last=res[1:]
print(*res_last)