基于MATLAB 水下航行器AUV/UUV 水下机器人MATLAB 六自由度基础数学模型（带参数）程序等

于 2025-02-25 15:15:55 发布
阅读量1k 收藏 17
点赞数 10
分类专栏： matlab 文章标签： matlab 机器人 开发语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2501_90314346/article/details/145853791
版权

基于MATLAB 水下航行器AUV/UUV 水下机器人MATLAB 六自由度基础数学模型（带参数）程序
在这里插入图片描述

文章目录


水下航行器（AUV/UUV）的六自由度数学模型通常包括位置和姿态的变化，这六个自由度分别是：沿X轴、Y轴、Z轴的平移运动以及绕这三个轴的旋转运动。下面提供一个简化的MATLAB代码示例，用于描述一个基础的六自由度数学模型。

六自由度数学模型

在建立六自由度模型时，我们首先需要定义航行器的位置向量 ( \mathbf{r} = [x, y, z]^T ) 和姿态角向量 ( \boldsymbol{\theta} = [\phi, \theta, \psi]^T )，其中 ( \phi ), ( \theta ), ( \psi ) 分别代表横滚角、俯仰角和偏航角。此外，还需要考虑速度向量 ( \mathbf{v} ) 和角速度向量 ( \boldsymbol{\omega} )。

动力学方程

水动力学方程可以分为两个部分：线性加速度和角加速度。

  • 线性加速度：[ \dot{\mathbf{v}} = \mathbf{M}^{-1} (\mathbf{f} - \mathbf{C}(\mathbf{v})\mathbf{v} - \mathbf{D}(\mathbf{v})\mathbf{v} + \mathbf{g}) ]
  • 角加速度：[ \dot{\boldsymbol{\omega}} = \mathbf{J}^{-1} (\mathbf{T} - \boldsymbol{\omega} \times \mathbf{J}\boldsymbol{\omega}) ]

其中：

  • ( \mathbf{M} ) 是质量矩阵。
  • ( \mathbf{f} ) 是作用力向量。
  • ( \mathbf{C}(\mathbf{v}) ) 和 ( \mathbf{D}(\mathbf{v}) ) 分别是科里奥利效应和阻尼效应矩阵。
  • ( \mathbf{g} ) 是重力/浮力向量。
  • ( \mathbf{J} ) 是转动惯量矩阵。
  • ( \mathbf{T} ) 是扭矩向量。

MATLAB 示例代码

以下是一个简化的MATLAB代码示例，用于模拟一个基本的六自由度AUV模型。

% 参数设置
m = 100; % 质量 (kg)
Ixx = 5; Iyy = 6; Izz = 7; % 转动惯量 (kg*m^2)
Xu = -50; Yv = -60; Zw = -70; % 线性阻尼系数 (N/(m/s))
Kp = -80; Mq = -90; Nr = -100; % 角速度阻尼系数 (N*m/(rad/s))

% 初始条件
x0 = [0, 0, 0]; % 初始位置 (m)
v0 = [0, 0, 0]; % 初始速度 (m/s)
theta0 = [0, 0, 0]; % 初始姿态角 (rad)
omega0 = [0, 0, 0]; % 初始角速度 (rad/s)

% 时间设置
tspan = [0 100]; % 时间范围 (s)
dt = 0.1; % 时间步长 (s)

% 定义状态变量
state0 = [x0, v0, theta0, omega0];

% ODE求解器
options = odeset('RelTol',1e-6,'AbsTol',1e-6);

[t, state] = ode45(@(t,state) dynamics(t, state, m, Ixx, Iyy, Izz, Xu, Yv, Zw, Kp, Mq, Nr), tspan, state0, options);

% 提取结果
x = state(:,1:3); % 位置
v = state(:,4:6); % 速度
theta = state(:,7:9); % 姿态角
omega = state(:,10:12); % 角速度

% 绘制结果
figure;
subplot(2,2,1);
plot(t, x); title('Position');
legend('x','y','z');

subplot(2,2,2);
plot(t, v); title('Velocity');
legend('vx','vy','vz');

subplot(2,2,3);
plot(t, theta); title('Orientation');
legend('\phi','\theta','\psi');

subplot(2,2,4);
plot(t, omega); title('Angular Velocity');
legend('\omega_x','\omega_y','\omega_z');

function dstate_dt = dynamics(~, state, m, Ixx, Iyy, Izz, Xu, Yv, Zw, Kp, Mq, Nr)
    % 解包状态变量
    x = state(1:3); % 位置
    v = state(4:6); % 速度
    theta = state(7:9); % 姿态角
    omega = state(10:12); % 角速度
    
    % 计算旋转矩阵 R_b_to_i
    phi = theta(1); theta_val = theta(2); psi = theta(3);
    R_b_to_i = [cos(theta_val)*cos(psi), sin(phi)*sin(theta_val)*cos(psi)-cos(phi)*sin(psi), cos(phi)*sin(theta_val)*cos(psi)+sin(phi)*sin(psi);
                cos(theta_val)*sin(psi), sin(phi)*sin(theta_val)*sin(psi)+cos(phi)*cos(psi), cos(phi)*sin(theta_val)*sin(psi)-sin(phi)*cos(psi);
                -sin(theta_val), sin(phi)*cos(theta_val), cos(phi)*cos(theta_val)];
    
    % 计算角速度到体坐标系的转换矩阵 T
    T = [1, sin(phi)*tan(theta_val), cos(phi)*tan(theta_val);
         0, cos(phi), -sin(phi);
         0, sin(phi)/cos(theta_val), cos(phi)/cos(theta_val)];
    
    % 力和扭矩
    f = [0; 0; 0]; % 外部力 (N)
    T = [0; 0; 0]; % 外部扭矩 (N*m)
    
    % 阻尼力和扭矩
    C_v = diag([Xu, Yv, Zw]);
    C_omega = diag([Kp, Mq, Nr]);
    D_v = C_v * v;
    D_omega = C_omega * omega;
    
    % 动力学方程
    dv_dt = inv(m) * (f - D_v);
    domega_dt = inv([Ixx, 0, 0; 0, Iyy, 0; 0, 0, Izz]) * (T - cross(omega, [Ixx, Iyy, Izz] .* omega));
    
    % 积分更新
    dx_dt = R_b_to_i * v;
    dtheta_dt = T * omega;
    
    % 返回导数
    dstate_dt = [dx_dt; dv_dt; dtheta_dt; domega_dt];
end

这段代码通过定义一个简单的六自由度动态模型来模拟AUV的运动，并使用ode45求解器进行数值积分。这个模型非常简化，实际应用中可能需要考虑更多因素，如非线性效应、流体动力学参数等。根据具体需求调整参数和模型结构将有助于获得更准确的结果。
在这里插入图片描述
假设这是一个典型的六自由度（6-DOF）水下航行器（AUV/UUV）模型的仿真结果。

假设的信号

  1. 第一个信号可能是线速度 ( v_x )。
  2. 第二个信号可能是线速度 ( v_y )。
  3. 第三个信号可能是线速度 ( v_z )。
  4. 第四个信号可能是角速度 ( \omega_z )。

MATLAB/Simulink 代码示例

1. 定义系统参数和初始条件
% 系统参数
m = 100; % 质量 (kg)
Ixx = 5; Iyy = 6; Izz = 7; % 转动惯量 (kg*m^2)
Xu = -50; Yv = -60; Zw = -70; % 线性阻尼系数 (N/(m/s))
Kp = -80; Mq = -90; Nr = -100; % 角速度阻尼系数 (N*m/(rad/s))

% 初始条件
x0 = [0, 0, 0]; % 初始位置 (m)
v0 = [0, 0, 0]; % 初始速度 (m/s)
theta0 = [0, 0, 0]; % 初始姿态角 (rad)
omega0 = [0, 0, 0]; % 初始角速度 (rad/s)

% 时间设置
tspan = [0 300]; % 时间范围 (s)
dt = 0.1; % 时间步长 (s)

% 定义状态变量
state0 = [x0, v0, theta0, omega0];
2. 定义动力学方程
function dstate_dt = dynamics(t, state, m, Ixx, Iyy, Izz, Xu, Yv, Zw, Kp, Mq, Nr)
    % 解包状态变量
    x = state(1:3); % 位置
    v = state(4:6); % 速度
    theta = state(7:9); % 姿态角
    omega = state(10:12); % 角速度
    
    % 计算旋转矩阵 R_b_to_i
    phi = theta(1); theta_val = theta(2); psi = theta(3);
    R_b_to_i = [cos(theta_val)*cos(psi), sin(phi)*sin(theta_val)*cos(psi)-cos(phi)*sin(psi), cos(phi)*sin(theta_val)*cos(psi)+sin(phi)*sin(psi);
                cos(theta_val)*sin(psi), sin(phi)*sin(theta_val)*sin(psi)+cos(phi)*cos(psi), cos(phi)*sin(theta_val)*sin(psi)-sin(phi)*cos(psi);
                -sin(theta_val), sin(phi)*cos(theta_val), cos(phi)*cos(theta_val)];
    
    % 计算角速度到体坐标系的转换矩阵 T
    T = [1, sin(phi)*tan(theta_val), cos(phi)*tan(theta_val);
         0, cos(phi), -sin(phi);
         0, sin(phi)/cos(theta_val), cos(phi)/cos(theta_val)];
    
    % 力和扭矩
    f = [0; 0; 0]; % 外部力 (N)
    T = [0; 0; 0]; % 外部扭矩 (N*m)
    
    % 阻尼力和扭矩
    C_v = diag([Xu, Yv, Zw]);
    C_omega = diag([Kp, Mq, Nr]);
    D_v = C_v * v;
    D_omega = C_omega * omega;
    
    % 动力学方程
    dv_dt = inv(m) * (f - D_v);
    domega_dt = inv([Ixx, 0, 0; 0, Iyy, 0; 0, 0, Izz]) * (T - cross(omega, [Ixx, Iyy, Izz] .* omega));
    
    % 积分更新
    dx_dt = R_b_to_i * v;
    dtheta_dt = T * omega;
    
    % 返回导数
    dstate_dt = [dx_dt; dv_dt; dtheta_dt; domega_dt];
end
3. 运行仿真
% ODE求解器
options = odeset('RelTol',1e-6,'AbsTol',1e-6);

[t, state] = ode45(@(t,state) dynamics(t, state, m, Ixx, Iyy, Izz, Xu, Yv, Zw, Kp, Mq, Nr), tspan, state0, options);

% 提取结果
x = state(:,1:3); % 位置
v = state(:,4:6); % 速度
theta = state(:,7:9); % 姿态角
omega = state(:,10:12); % 角速度

% 绘制结果
figure;
subplot(2,2,1);
plot(t, v(:,1)); title('Linear Velocity in X');
legend('vx');

subplot(2,2,2);
plot(t, v(:,2)); title('Linear Velocity in Y');
legend('vy');

subplot(2,2,3);
plot(t, v(:,3)); title('Linear Velocity in Z');
legend('vz');

subplot(2,2,4);
plot(t, omega(:,3)); title('Angular Velocity in Z');
legend('\omega_z');

说明

  • dynamics 函数：定义了六自由度的动力学方程。
  • ode45 求解器：用于数值积分，求解微分方程。
  • plot 函数：用于绘制仿真结果。

在这里插入图片描述
假设这是一个典型的六自由度（6-DOF）水下航行器（AUV/UUV）模型的仿真结果。

假设的信号

  1. 第一个信号可能是线速度 ( v_x )。
  2. 第二个信号可能是线速度 ( v_y )。
  3. 第三个信号可能是线速度 ( v_z )。
  4. 第四个信号可能是角速度 ( \omega_z )。

MATLAB/Simulink 代码示例

1. 定义系统参数和初始条件
% 系统参数
m = 100; % 质量 (kg)
Ixx = 5; Iyy = 6; Izz = 7; % 转动惯量 (kg*m^2)
Xu = -50; Yv = -60; Zw = -70; % 线性阻尼系数 (N/(m/s))
Kp = -80; Mq = -90; Nr = -100; % 角速度阻尼系数 (N*m/(rad/s))

% 初始条件
x0 = [0, 0, 0]; % 初始位置 (m)
v0 = [0, 0, 0]; % 初始速度 (m/s)
theta0 = [0, 0, 0]; % 初始姿态角 (rad)
omega0 = [0, 0, 0]; % 初始角速度 (rad/s)

% 时间设置
tspan = [0 300]; % 时间范围 (s)
dt = 0.1; % 时间步长 (s)

% 定义状态变量
state0 = [x0, v0, theta0, omega0];
2. 定义动力学方程
function dstate_dt = dynamics(t, state, m, Ixx, Iyy, Izz, Xu, Yv, Zw, Kp, Mq, Nr)
    % 解包状态变量
    x = state(1:3); % 位置
    v = state(4:6); % 速度
    theta = state(7:9); % 姿态角
    omega = state(10:12); % 角速度
    
    % 计算旋转矩阵 R_b_to_i
    phi = theta(1); theta_val = theta(2); psi = theta(3);
    R_b_to_i = [cos(theta_val)*cos(psi), sin(phi)*sin(theta_val)*cos(psi)-cos(phi)*sin(psi), cos(phi)*sin(theta_val)*cos(psi)+sin(phi)*sin(psi);
                cos(theta_val)*sin(psi), sin(phi)*sin(theta_val)*sin(psi)+cos(phi)*cos(psi), cos(phi)*sin(theta_val)*sin(psi)-sin(phi)*cos(psi);
                -sin(theta_val), sin(phi)*cos(theta_val), cos(phi)*cos(theta_val)];
    
    % 计算角速度到体坐标系的转换矩阵 T
    T = [1, sin(phi)*tan(theta_val), cos(phi)*tan(theta_val);
         0, cos(phi), -sin(phi);
         0, sin(phi)/cos(theta_val), cos(phi)/cos(theta_val)];
    
    % 力和扭矩
    f = [0; 0; 0]; % 外部力 (N)
    T = [0; 0; 0]; % 外部扭矩 (N*m)
    
    % 阻尼力和扭矩
    C_v = diag([Xu, Yv, Zw]);
    C_omega = diag([Kp, Mq, Nr]);
    D_v = C_v * v;
    D_omega = C_omega * omega;
    
    % 动力学方程
    dv_dt = inv(m) * (f - D_v);
    domega_dt = inv([Ixx, 0, 0; 0, Iyy, 0; 0, 0, Izz]) * (T - cross(omega, [Ixx, Iyy, Izz] .* omega));
    
    % 积分更新
    dx_dt = R_b_to_i * v;
    dtheta_dt = T * omega;
    
    % 返回导数
    dstate_dt = [dx_dt; dv_dt; dtheta_dt; domega_dt];
end
3. 运行仿真
% ODE求解器
options = odeset('RelTol',1e-6,'AbsTol',1e-6);

[t, state] = ode45(@(t,state) dynamics(t, state, m, Ixx, Iyy, Izz, Xu, Yv, Zw, Kp, Mq, Nr), tspan, state0, options);

% 提取结果
x = state(:,1:3); % 位置
v = state(:,4:6); % 速度
theta = state(:,7:9); % 姿态角
omega = state(:,10:12); % 角速度

% 绘制结果
figure;
subplot(2,2,1);
plot(t, v(:,1)); title('Linear Velocity in X');
legend('vx');

subplot(2,2,2);
plot(t, v(:,2)); title('Linear Velocity in Y');
legend('vy');

subplot(2,2,3);
plot(t, v(:,3)); title('Linear Velocity in Z');
legend('vz');

subplot(2,2,4);
plot(t, omega(:,3)); title('Angular Velocity in Z');
legend('\omega_z');

说明

  • dynamics 函数：定义了六自由度的动力学方程。
  • ode45 求解器：用于数值积分，求解微分方程。
  • plot 函数：用于绘制仿真结果。

请根据您的具体需求调整参数和模型结构。如果您有更具体的模型或参数，请提供详细信息，以便进一步优化代码。

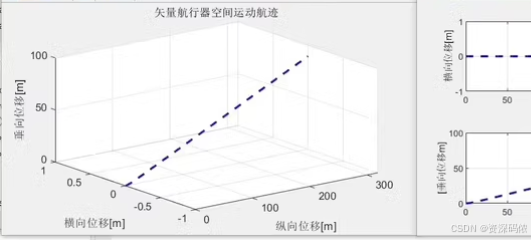
三维轨迹绘制

% 绘制三维轨迹
figure;
plot3(x(:,1), x(:,2), x(:,3), 'b.-');
xlabel('横向位移 (m)');
ylabel('纵向位移 (m)');
zlabel('垂向位移 (m)');
title('矢量航行器空间运动轨迹');
grid on;

这样，您可以得到三维空间中的运动轨迹图。希望这些代码和说明对您有所帮助！

毕设题目：Matlab飞行器
订阅付费专栏Matlab（奶茶价版），可赠送奶茶价版付费专栏指定代码1份；
11-27 982
毕设题目：Matlab飞行器 完整代码，直接运行，适合小白！可提供运行操作视频！
【AUV模型】基于matlab水下机器人AUV 六自由度模型（含位移 速度 航迹）【含Matlab源码 8044期】.mp4
09-28
Matlab领域上传的视频均有对应的完整代码，皆可运行，亲测可用，适合小白； 1、代码压缩包内容 主函数：main.m； 调用函数：其他m文件；无需运行 运行结果效果图； 2、代码运行版本 Matlab 2019b；若运行有误，根据提示修改；若不会，私信博主； 3、运行操作步骤 步骤一：将所有文件放到Matlab的当前文件夹中； 步骤二：双击打开main.m文件； 步骤三：点击运行，等程序运行完得到结果； 4、仿真咨询 如需其他服务，可私信博主或扫描视频QQ名片； 4.1 博客或资源的完整代码提供 4.2 期刊或参考文献复现 4.3 Matlab程序定制 4.4 科研合作
【无人潜水器】UUV的仿真和控制（Matlab实现）
weixin_67304359的博客
08-18 808
UUV（Unmanned Underwater Vehicle，无人水下航行器）是一种能够在水下环境中自主或遥控操作的设备。UUV广泛应用于海洋科学研究、资源勘探、军事侦察、水下搜救等多种领域。UUV的设计与开发涉及多个技术领域，其中仿真技术和控制系统是两个非常关键的部分。UUV的仿真与控制技术通常紧密结合，在开发过程中需要不断地迭代优化。仿真平台可以帮助工程师在真实环境下测试之前就发现并解决潜在问题，从而减少实际试验的成本和风险。而良好的控制系统则是保证UUV高效完成任务的关键因素之一。
可发射回收的“Yellow Moray”UUV简介
qq_50761331的博客
12-25 250
可发射回收的“Yellow Moray”UUV简介，希望为水下研究者提供参考。
【无人水下航行器】(UUV)与(UAS)的空间与时间会合（Matlab实现）
weixin_67304359的博客
12-16 590
UUV是一种能够在水下自主或遥控航行的无人平台，根据控制方式可分为遥控型水下航行器（ROV）和自主式水下航行器（AUV）。UUV具有小型化、智能化、机动范围大和隐蔽性好等特点，可用于水下警戒、侦察、监视、跟踪、探雷、布雷、中继通信和隐蔽攻击等多种任务。
无人水下航行器(UUV)仿真研究（Matlab代码实现）
weixin_67304359的博客
07-16 1272
无人水下航行器（UUV）的仿真研究是指利用计算机模拟和仿真技术对UUV进行模拟和测试的活动。这种研究可以帮助开发人员更好地了解UUV的性能、操控特性和系统行为，从而指导设计优化、控制算法开发和任务规划等方面的工作。以下是进行UUV仿真研究时可能涉及的一些关键方面：1. **动力系统仿真：** 模拟UUV的推进系统，包括水声发动机、螺旋桨、舵和电池等，以评估其功耗、速度性能和续航能力。2. **水动力学仿真：** 通过数值方法模拟UUV在水下的运动特性，包括水下航行时的阻力、操纵性能和稳定性。
水下航行器(UUV/AUV)纵垂面深度跟踪控制的MATLAB Simulink反演滑膜控制实现与仿真
最新发布
04-18
内容概要：本文详细介绍了利用反演滑膜控制实现水下航行器(UUV/AUV)纵垂面深度跟踪的方法及其在MATLAB Simulink中的实现。主要内容涵盖系统建模、控制器设计、参数调整以及仿真实验。反演滑膜控制结合了反演控制和...
6自由度AUV的matlab仿真
09-21
这是基于matlab对AUV的模型仿真，无缆水下机器人的英文缩写。 水下工程设备，水下机器人的一种。习惯称为自主式水下潜器(Autonomous Underwater Vehicle，简称AUV)。 水下机器人主要分为两大类：一类是有缆水下...
MATLAB Simulink控制仿真：欠驱动UUV-AUV六自由度模型指南
在水下航行器的背景下，这意味着航行器有六个自由度（六自由度模型：沿x、y、z轴的移动和绕这三个轴的旋转），但控制输入（如推力和舵面控制）可能少于六个。这导致欠驱动系统控制更为复杂。 #### 3. MATLAB ...
AUV 六自由度模型 MATLAB 仿真
05-19
AUV 六自由度模型 MATLAB 仿真
无人水下航行器（UUV）的技术发展
06-05
近年来，由于科学技术的进步和军事作战观念的变化，武器系统发生了巨大变化。 所有这些变更的核心是一个无人驾驶系统。 特别是在海洋环境下，由于作战的中心阶段已从海洋转移到沿海地区，现有海军很难在浅水区有效作战。 因此，无人驾驶水下航行器（UUV）的需求正在日益增长。 在本文中，我们分析了已经开发的UUV的特征，它们是未来海洋战场环境中的关键无人系统。 通过对开发案例的分析和对关键技术的研究，阐述了UUV的关键设计问题。 我们还根据案例分析提出UUV技术的未来方向。
【UUV控制】基于龙格库塔法无人水下航行器UUV六自由度运动Matlab仿真（含速度 位移 艏向角 纵倾角）
Matlab_jiqi的博客
01-26 594
无人水下航行器（UUV）在海洋探索、资源开发、军事应用等领域扮演着日益重要的角色。精确的运动建模是UUV控制的基础。本文深入探讨了基于龙格-库塔法求解UUV六自由度运动方程，并详细阐述了速度、位移、艏向角、纵倾角的动力学建模过程。通过建立精确的数学模型，并采用龙格-库塔法进行数值求解，可以为UUV的控制算法设计、仿真分析以及实际应用提供可靠的理论基础和技术支持。本文旨在为相关领域的学者和工程师提供一份全面且深入的参考。引言无人水下航行器（UUV）是一种能够在水下自主或遥控执行任务的智能机器人。
异构系统中的UUV、异构系统模型统一化及单应矩阵在异构系统中的应用
qq_45830323的博客
11-15 891
主要做法是在跟踪前获取设定的图像信息，在跟踪过程中，利用设定的图像信息和当前的图像信息计算出单应性矩阵Hc，再对该矩阵进行奇异值分解，得到UAV与船舶的相对旋转矩阵，从而为设计控制器提供依据。文献[7]中虽然也是首先统一异构系统的模型，但不同于前面文献[3-6]引入虚拟控制量的方式，文献[7]是通过选取合适的状态变量，将异构系统表示成形式一样的线性状态空间模型。同样对另一异构模型，做同样的操作引入虚拟控制量，便可以得到如式（3）所示的形式，从而实现模型的统一化，为后续设计控制器奠定基础。
无人机6自由度仿真模型简介
热门推荐
Apache_mm的博客
11-06 3万+
无人机6自由度仿真模型简介      本文使用的是simulink 中的飞行器设计框架搭建的无人机的仿真模型。    大致的仿真步骤如下图所示：           在Simulink中提供了航空宇航模块 Aerospace Blockset, 它是用于在 Simulink中进行航空航天飞行器建模、 集成与仿真的模块。 Aerospace Blockset将航
UUV、AUV和ROV
06-17 6884
 
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值