基于多元线性回归（MLR）与径向基函数神经网络（RBFNN）组合模型的纯电动汽车能耗预测

于 2025-05-19 07:30:00 发布
阅读量641 收藏 12
点赞数 31
文章标签： 线性回归 神经网络 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2501_90583334/article/details/148024052
版权
#新星杯·14天创作挑战营·第11期#

引言：为什么能耗预测是纯电动汽车的“命门”？

纯电动汽车的续航里程焦虑一直是制约其普及的核心问题。根据行业数据，70%的潜在消费者因续航不足放弃购买。而续航里程的准确性直接依赖能耗预测模型的精度。传统单一模型（如线性回归）难以捕捉复杂的非线性因素（如温度、驾驶行为），导致预测误差较大。本文将解析一种多元线性回归（MLR）与径向基函数神经网络（RBFNN）的组合模型，通过工程实践验证其显著提升预测精度的能力。

第一篇 多元线性回归（MLR）：原理、流程与工程应用详解

一、什么是多元线性回归？

多元线性回归（Multiple Linear Regression, MLR）是一种统计建模方法，用于研究一个因变量（目标）与多个自变量（特征）之间的线性关系。其核心目标是找到一组最优的回归系数，使得模型能够准确预测因变量的值。
公式表示：
在这里插入图片描述

二、MLR建模全流程（附流程图）

流程图
数据收集
数据预处理
模型构建
参数估计
假设检验
模型评估
应用与优化

步骤详解

  1. 数据收集

    • 采集与目标相关的多维度数据。例如，纯电动汽车能耗预测需包括：
      • 行驶参数：速度、加速度、坡度
      • 环境参数：温度、风速
      • 电池参数：电压、电流、SOC（电池荷电状态）

  2. 数据预处理

    • 缺失值处理：删除或插补（如均值填充）。

    • 异常值处理：3σ原则或箱线图筛选。

    • 标准化/归一化：消除量纲差异。
      在这里插入图片描述

    • 多重共线性检测：通过VIF（方差膨胀因子）判断，若VIF >10，需删除或合并相关变量。

  3. 模型构建

    • 确定自变量与因变量的数学关系。例如：
      在这里插入图片描述

  4. 参数估计

    • 使用**最小二乘法（OLS）**求解回归系数，目标是最小化残差平方和：
      在这里插入图片描述
      在这里插入图片描述

  5. 假设检验

    • t检验：检验单个回归系数是否显著。 在这里插入图片描述

    • F检验：验证模型整体显著性（至少一个自变量显著）。

    • 显著性水平：通常取(\alpha=0.05)，若p值<0.05则拒绝原假设。

  6. 模型评估

    • R²（决定系数）：解释模型对因变量的方差贡献，R²越接近1，拟合越好。
    • 调整R²：惩罚过多自变量，避免过拟合。
    • 残差分析：检查残差是否服从正态分布、是否异方差。

  7. 应用与优化

    • 预测新数据：输入自变量，输出因变量预测值。
    • 优化方向：
      • 添加交互项（如速度×温度）捕捉复杂关系。
      • 使用正则化（Lasso/Ridge）解决过拟合。

三、MLR的局限性及应对策略

  1. 线性假设限制：无法捕捉非线性关系（如温度平方项需手动添加）。
    • 解决方案：与神经网络组合（如MLR+RBFNN）。
  2. 多重共线性问题：自变量高度相关导致系数不稳定。
    • 解决方案：VIF检测后剔除冗余变量，或使用主成分回归（PCR）。

多元线性回归是能耗预测的基石，优势在于解释性强、计算高效，但需结合领域知识优化变量选择。在工程实践中，MLR常作为组合模型的“第一层”，用于捕捉主要线性趋势，再通过其他模型（如神经网络）补偿残差，实现高精度预测。

第二篇 径向基函数神经网络（RBFNN）：原理、流程与实战解析

一、什么是RBF神经网络？

径向基函数神经网络（Radial Basis Function Neural Network, RBFNN）是一种三层前馈网络，擅长解决局部非线性问题。其核心思想是：通过隐含层的径向基函数（如高斯函数）对输入数据进行非线性映射，再通过输出层的线性组合实现复杂函数逼近。
优势：训练速度快、结构简单、适合高维数据。
劣势：隐含层节点数敏感，中心选择影响性能。

二、RBFNN结构与数学原理

网络结构
输入层
隐含层: 径向基函数
输出层: 线性加权和
  1. 输入层：接收原始数据（如速度、温度），节点数=特征维度。
    在这里插入图片描述

三、RBFNN训练全流程（附流程图）

流程图
数据预处理
确定隐含层中心
计算隐含层宽度
求解输出层权重
模型验证与调优

步骤详解

  1. 数据预处理

    • 归一化：将输入数据缩放到[0,1]或[-1,1]，消除量纲影响。
      在这里插入图片描述

    • 划分数据集：70%训练集、15%验证集、15%测试集。

  2. 确定隐含层中心

    • K均值聚类：将训练数据聚类，类心作为隐含层中心(\mathbf{c}_j)。
    • 随机选择：随机选取部分训练样本作为中心（适合小数据集）。
    • 先验知识：根据问题领域手动指定（如温度分段中心）。

  3. 计算隐含层宽度

    • 经验公式：在这里插入图片描述
      ，其中dmax是中心间最大距离，(m)为隐含层节点数。
    • 优化算法：通过梯度下降或遗传算法调整σj。

  4. 求解输出层权重

    • 最小二乘法：直接计算权重矩阵W，公式：
      在这里插入图片描述

      • H：隐含层输出矩阵
      • Y：目标输出向量

  5. 模型验证与调优

    • 评价指标：均方误差（MSE）、平均绝对误差（MAE）。
    • 调优策略：
      • 增加隐含层节点数以提升拟合能力（可能过拟合）。
      • 调整高斯函数宽度σj平衡平滑性与灵敏度。

四、RBFNN在能耗预测中的实战案例

场景：补偿多元线性回归（MLR）模型的非线性残差

  1. 输入数据：
    • MLR预测值、环境温度（归一化后）。
  2. 隐含层设计：
    • 中心数(m=10)（通过K均值聚类确定）。
    • 宽度σj=0.5（经验公式计算）。
  3. 输出层：
    • 目标值为MLR模型的残差（实际值 - MLR预测值）。
  4. 结果：
    • 组合模型（MLR+RBFNN）平均误差从4.32%降至2.97%。

五、RBFNN的工程应用与注意事项

应用场景

  • 非线性回归：如电池SOC估计、电机效率拟合。
  • 模式分类：如驾驶行为识别（激进/保守）。
  • 时序预测：结合滑动窗口处理能耗时序数据。

注意事项

  1. 隐含层节点数：过少导致欠拟合，过多引发过拟合（需交叉验证）。
  2. 中心选择：推荐使用聚类算法（如K均值）代替随机选择。
  3. 实时性：RBFNN推理速度快，适合车载嵌入式部署。

六、RBFNN与其他神经网络的对比

特性RBFNNBP神经网络LSTM
训练速度快（单次最小二乘）慢（需反向传播迭代）慢（时序依赖计算复杂）
非线性能力局部非线性全局非线性时序非线性
参数敏感度中心与宽度敏感学习率、层数敏感时间步长敏感
适用场景静态非线性问题通用模型时序依赖问题

七、总结

RBFNN通过局部感知和快速训练的特性，成为解决工程非线性问题的利器。在新能源汽车领域，其与线性模型的组合（如MLR+RBFNN）能显著提升预测精度。核心要点：合理选择隐含层中心与宽度，平衡模型复杂度与泛化能力。

第三篇 基于多元线性回归（MLR）与径向基函数神经网络（RBFNN）组合模型的纯电动汽车能耗预测

一、纯电动汽车能耗的“三大流向”

纯电动汽车的能耗并非仅用于行驶，其能量流向可分解为三部分：

1. 行驶阻力能耗（占比约60%-80%）

  • 公式：
    在这里插入图片描述

  • 通俗解释：车辆需克服地面摩擦、爬坡阻力和空气阻力，高速行驶时空气阻力占比显著上升（与速度平方成正比）。

2. 制动能量回收（回收效率约15%-30%）

  • 公式：
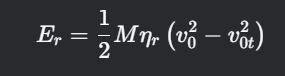
    在这里插入图片描述

    其中，ηr为制动回收效率。

  • 关键点：能量回收效率受电池状态、制动强度限制，频繁启停场景回收效果更佳。

3. 附件能耗（占比约10%-30%）

  • 公式：
    在这里插入图片描述

    pa为附件功率（如空调、车机系统），低温制热工况下空调能耗可飙升3倍。

二、数据采集：从CAN总线到云端监控

1. 车载数据采集系统架构

[车载终端] → [CAN总线数据] → [4G模块] → [云端服务器] → [数据库]
  • 核心硬件：英飞凌TC275主控芯片（高性能实时处理）、U9300 4G模块（支持GPS定位）。
  • 关键数据：速度、加速度、电池电压/电流、温度、海拔差（通过Google Maps API获取）。

2. 数据预处理

  • 片段划分：每5秒为一个片段，计算平均速度、加速度、百公里能耗（公式：(E_{bat} = \int V_t I_t , dt / \text{行驶里程})）。
  • **示例数据：
    速度(m/s)加速度(m/s²)海拔差(m)百公里能耗(kWh/100km)
    13.65-0.86226.82

三、组合模型原理：线性回归 + 神经网络的“双剑合璧”

1. 多元线性回归（MLR）模型

  • 公式：
    在这里插入图片描述

    • (T)为环境温度，二次项捕捉U型关系（低温/高温均增加能耗）。

  • 参数估计：

    参数估计值t值显著性
    β₁0.87352.230.000
    λ₁0.020-4.890.013

2. RBF神经网络补偿非线性残差

  • 网络结构：

    输入层（2节点：MLR预测值 + 温度） → 隐含层（高斯核函数） → 输出层（残差）

  • 高斯核函数：
    在这里插入图片描述

  • 训练流程：

    1. 数据归一化（Min-Max Scaling）
    2. 使用MATLAB newrbe函数自动优化隐含层节点数。

3. 组合模型工作流程
原始数据
MLR模型
线性预测值
RBFNN
非线性残差
最终预测值 = 线性预测 + 残差

四、实验结果：误差从4.32%降至2.97%

1. 性能对比

模型最大误差平均误差
单一MLR5.89%4.32%
MLR+RBFNN3.95%2.97%

五、行业应用与未来展望

1. 应用场景

  • 续航里程实时估算：结合导航数据动态调整剩余里程显示。
  • 智能充电规划：根据能耗预测推荐最佳充电时机。
  • 车队能耗管理：物流企业优化路线与电池调度。

2. 技术延伸

  • 融合LSTM神经网络捕捉时序特征（如拥堵路况）。
  • 引入边缘计算实现车载端实时预测。

六、讨论：你认为哪些因素最影响电动汽车能耗？

欢迎在评论区留言，分享你的观察或实践案例。关注我的专栏，获取更多新能源汽车硬核技术解析！🔥

关键词：纯电动汽车能耗预测、RBF神经网络、多元线性回归、续航里程优化
相关标签：#新能源汽车 #人工智能 #算法优化 #电池管理

十一、机器学习进阶知识：径向基神经网络（RBFNN）的实现（Python，附源码及数据集）
weixin_42051846的博客
01-29 1万+
本文对径向基神经网络（RBFNN）的理论基础及建模步骤进行介绍，之后使用Python实现基于RBFNN的数据预测，通俗易懂，适合新手学习，附源码及实验数据集。
深度学习之径向基函数神经网络RBFNN
热门推荐
liuy9803的博客
08-08 3万+
  径向基函数（Radial Basis Function）神经网络是具有唯一最佳逼近（克服局部极小值问题）、训练简洁、学习收敛速度快等良好性能的前馈型神经网络，目前已证明RBFNN能够以任意精度逼近任意连续的非线性网络，被广泛用于函数逼近、语音识别、模式识别、图像处理、自动控制和故障诊断等领域。 全局逼近网络：网络的一个或多个权值对任一输出都有影响。由于每次输入都要对所有权值进行修正，因此这...
模型预测控制（MPC）在混合动力汽车能量管理策略开发上的运用。 [1]利用车速预测模型（BP或者RBF神经
YyuWmFvY的博客
03-06 437
动态规划算法作为全局优化的代表，可以与MPC相结合，实现基于模型预测的能量管理策略的预测时预内的局部最优近似全局最优的优化效果。[2]动态规划算法作为全局优化的代表，恰好作为模型预测控制的算法求解器，再与车速预测模型结合实现基于模型预测（MPC）的能量管理策略的预测时预内的局部最优近似全局最优的优化效果，实现混动车辆的燃油经济性最优！好的，根据您提供的主题和要求，我将为您撰写一篇关于“模型预测控制（MPC）在混合动力汽车能量管理策略开发上的运用”的技术博客文章。二、模型预测控制（MPC）的应用。
多元线性回归（MLR）预测模型及其Python和MATLAB实现
qq_45441438的博客
08-06 1089
这两个实现展示了如何在Python和MATLAB中构建和评估多元线性回归模型。y = 3 + 2 * X[:, 0] + 3 * X[:, 1] + np.random.randn(100) # 生成y值。X = np.random.rand(100, 5) # 100个样本和5个特征。fprintf('均方误差 (MSE): %.4f\n', mse);
MLR（mixed logistic regression）模型
很吵请安静
04-26 7178
基本形式 MLR模型是阿里巴巴12年提出（17年发表）点击率预估模型，它利用分段方式对数据进行拟合，相比LR模型，能够学习到更高阶的特征组合。其基本表达式如下 p(y=1∣x)=g(∑j=1mσ(ujTx)η(wjTx))(1) p(y=1 | x)=g\left(\sum_{j=1}^{m} \sigma\left(u_{j}^{T} x\right) \eta\left(w_{j}^{T} x...
多元线性回归MLR多变量预测模型，多变量输入结构，可以拟合出方程，评价指标包括:R2、MAE、MSE、RMSE等，代码质量极高，方便学习和替换数据。
机器学习-深度学习
04-17 480
多元线性回归MLR多变量预测模型，多变量输入结构，可以拟合出方程，评价指标包括:R2、MAE、MSE、RMSE等，代码质量极高，方便学习和替换数据。
【回归预测】MLR多元线性回归-MATLAB
2303_77200324的博客
02-16 1357
在数据分析和机器学习领域，回归分析是一种广泛应用于预测和建立模型的技术。本文将探讨如何利用多元线性回归模型进行数据预测，并通过MATLAB实现其在实际数据集上的应用。多元线性回归通过建立自变量与因变量之间的线性关系，能够帮助我们预测未知数据的结果，广泛应用于经济学、工程学、医学等多个领域。 本文将详细介绍多元线性回归的基本原理、相关公式、模型训练过程，并通过代码实现模型的建立、预测以及评估。我们将以一个实际数据集为例，展示如何使用MATLAB进行数据的预处理、回归模型的训练、结果预测及模型
MLR算法[Paper笔记]
weixin_33868027的博客
12-10 862
介绍 MLR算法是alibaba在2012年提出并使用的广告点击率预估模型，2017年发表出来。 如下图，LR不能拟合非线性数据，MLR可以拟合非线性数据，因为划分-训练模式。 　　 讨论，非线性拟合能力： 数据划分规则如下公式，特征分片数m=1时，退化为LR；上图MLR中m=4。m越大，模型的拟合能力越强，一般m=12。 　　　　 基础知识 优化方...
【漫话机器学习系列】178.多元逻辑回归（Multinomial Logistic Regression）
最新发布
IT古董
04-03 1106
在机器学习和统计建模中，分类问题是一类常见的任务，尤其是多分类问题（multi-class classification）。当需要对一个数据点归类到多个类别之一时，普通的逻辑回归（Logistic Regression）已经无法满足需求，而 多元逻辑回归（Multinomial Logistic Regression，简称 MLR） 就是一种扩展后的方法，可以有效地处理这类问题。
基于AR模型及MLR模型的汽车行驶姿态预测 (2014年)
05-15
运用自回归(AR)建模预测方法及多层递阶(MLR)建模预测方法对汽车行驶姿态进行预测。在详细分析了两种的建模预测方法的基础上,以汽车的侧倾角速度预测为例讨论了两种建模预测方法在汽车行驶姿态预测中的应用。结果显示AR 建模预测方法有一定的预测效果,1 s 预测平均相对误差为10.56%,MLR 建模预测方法由于充分考虑到了汽车运动的时变性和非线性特性,其预测效果更佳,1 s 及2 s 的预测精度分别比AR 建模预测法提高6.44%和7.09%。
深度学习与推荐系统（十五）——LS-PLM（MLR）模型
livan1234的博客
09-15 2795
CTR预估的发展过程中，LR模型是比较常用的方法，因为其计算量小容易并行，工业上应用非常广泛，同时也引发了各位大佬基于LR模型的优化改进，这一改进通常有两个方向，一个是走融合路，即GBDT+LR样式，将LR模型与其他的模型算法结合，达到优势互补的效果；另一个就是因子分解，即FM系列探索，它们的主要思想就是构造交叉特征或者是二阶的特征来一起进行训练。 除此之外也会有一些大佬给出一些新的思路，比如本文中介绍的LS-PLM模型（又叫MLR模型），这一模型是用传统的机器学习方法模仿了深度学习的结构，采用divid
二阶系统级联_（读论文）推荐系统之CTR预估-MLR算法模型
weixin_39808953的博客
11-28 314
本人才疏学浅，不足之处欢迎大家指出和交流。文有配图... 放假迟更几天，今天继续带来传统模型之MLR算法模型，这是一篇来自阿里盖坤团队的方案（LS-PLM），发表于2017年，但实际在2012年就已经提出并应用于实际业务中（膜拜ing），当时主流仍然是我们上一篇提到过的的LR模型，而本文作者创新性地提出了MLR(mixed logistic regression, 混合逻辑斯特回归)算法，引领...
闲聊DNN CTR预估模型
weixin_34406061的博客
08-03 421
原文：http://www.52cs.org/?p=1046 闲聊DNN CTR预估模型 Written by b manongb 作者：Kintocai， 北京大学硕士， 现就职于腾讯。 伦敦大学张伟楠博士在携程深度学习Meetup[1]上分享了Talk《Deep Learning over Multi-field Categorical Data – A Case Study ...
MLR（mixed logistic regression）算法原理及实现
惠小惠
05-29 1万+
MLR（mixed logistic regression）算法 参考https://zhuanlan.zhihu.com/p/77798409?utm_source=wechat_session 原文：《Learning Piece-wise Linear Models from Large Scale Data for Ad Click Prediction》 MLR算法创新地提出并实现了直接在原始空间学习特征之间的非线性关系 MLR算法模型，这是一篇来自阿里盖坤团队的方案（LS-PLM），发表于2
回归模型的不稳定性
CoderPai的博客
11-02 7588
作者：chen_h 微信号 &amp; QQ：862251340 微信公众号：coderpai 介绍 由于各种原因，回归系数可能存在且不稳定。这篇文章会简单介绍这种情况。 回归分析允许我们估计函数中的系数，该函数用于设计的多个数据集。我们假设这个函数的一个特定形式，然后找到适合数据的系数，假设偏离模型可以被认为是噪声。 在构建这样的模型时，我们接受它不能完美的预测因变量。在这里，我们想要评估模型...
从ctr预估问题看看f(x)设计—DNN篇
Bryan__的专栏
08-24 7141
转自：https://zhuanlan.zhihu.com/p/28202287 把DNN引入ctr预估无非看重两点： 一，改进模型结构，提高“信息利用率”，发现高阶非线性特征，挖掘以前挖不到潜在模式，比如DIN引入attention机制；一般来说Embedding+MLP是标配。 二，扩充“信息量”，把图片/文本这类不好处理的数据利用起来，比如DeepCTR； #0 RoadMa
机器学习的R实现（mlr包）
Christina
08-20 3343
https://www.analyticsvidhya.com/blog/2016/08/practicing-machine-learning-techniques-in-r-with-mlr-package/ Table of Content Getting Data Exploring Data Missing Value Imputation Feature Engineering Outlier Removal by Capping New Features Machine
基于MLR资讯多分类
baymax_007的博客
09-17 1948
针对海量资讯，通过机器学习实现多分类，从而减轻人工打标工作量，具有重要意义。 资讯分类可以拆解为两个问题： 文本分词，提取特征 多分类模型 针对文本分词，常见中文分词工具有：HanLP、ansj、jieba和fudannlp。这里选取HanLP。而多分类模型有逻辑回归（Logistic regression）、决策树（Decision tree classifier）、随机森林（Random...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值