(第一章)深度学习标准化技术综述: 从BatchNorm到DeepNorm的演进与实战

最新推荐文章于 2025-06-05 16:53:26 发布

Shannon@

最新推荐文章于 2025-06-05 16:53:26 发布

阅读量1k

点赞数 29

文章标签：深度学习归一化技术 BatchNorm DeepNorm LayerNorm Transformer 模型优化

本文链接：https://blog.csdn.net/2501_91903104/article/details/148410084

版权

#王者杯·14天创作挑战营·第2期#

Normalization作用是通过标准化隐藏层的输出，稳定训练过程，缓解梯度消失或爆炸问题，同时加速收敛并提高模型泛化能力

这里的“Add”就是残差操作，缓解深层网络梯度消失问题

Normalization（归一化）：目的是通过对激活值或特征张量进行规范化处理，使得缓解梯度消失、加速模型收敛、增强模型泛化能力.

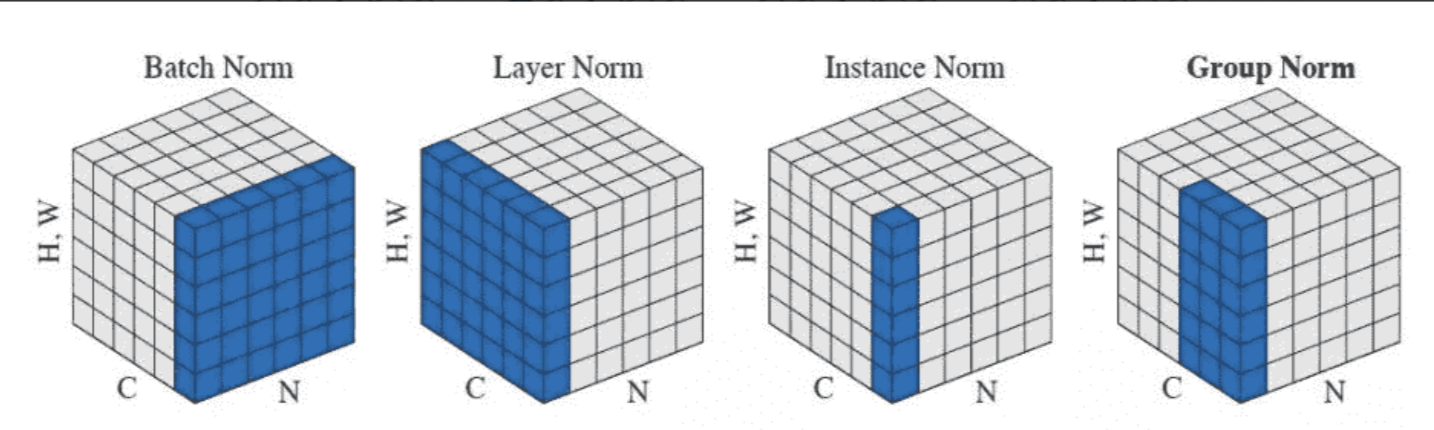
又有其它多种归一化技术，如Batch Normalization(BN)、Layer Normalization(LN)、Instance Normalization(IN)、Group Normalization(GN)、RMS Norm以及超深层模型有效的Deep Norm等。

BatchNorm

为什么进行BN?

深度神经网络训练过程中，采用mini-batch进行梯度下降时，每个batch数据分布不同，使得网络各层的输入分布在训练过程中不断发生漂移（ICS），使得模型训练变得困难，收敛速度变慢。

ICS是指前面batch训练时会影响到后续batch的训练，让模型在这条道路一直训练，起了形象的名字——漂移。

BN核心思想是在激活函数前，对每个通道在batch维度上计算均值与方差，并将激活值约束到均值为0、方差为1的分布 （再加上可学习的缩放与偏置系数），可减小ICS问题

BN的计算过程

如果某层输出维度为[N,C,H,W]，其中N表示batch_size,C为通道数，H和W分别为表示特征图的高和宽。

沿着通道方向计算每个batch的均值和方差，即对同一通道内的所有样本像素进行统计：

1.计算均值\ $\mu_c$ ： $\mu_c = \frac{1}{N\times H\times W}\sum_{n=1}^N \sum_{h=1}^H\sum_{w=1}^W x_{n,c,w,h}$

2.计算方差 $\sigma_c^2$ : $\sigma_c^2=\frac{1}{N\times H\times W\times}\sum_{n=1}^N \sum_{h=1}^H \sum_{w=1}^W (x_{n,c,h,w}-\mu_c)^2$

3.归一化 $\hat{x}_{n,c,h,w}$ : $\hat{x}_{n,c,h,w}=\frac{x_{n,c,h,w}-\mu_c}{\sqrt{\sigma^2+\epsilon}}$

$\epsilon$ 是一个非常小的正数，它的作用是防止分母为零或接近零的情况，从而避免计算时出现数值不稳定或错误。

4.缩放和平移： $y_{h,c,w,h}=\gamma_c \hat{x}_{n,c,w,h}+\beta_c$ ,其中 $\gamma_c, \beta_c$ 为可学习参数，初始时 $\gamma_c=1,\beta_c=0$

BN的作用

减少ICS,避免梯度消失、爆炸
允许使用较大的学习率
降低对权重初始化的敏感度
对隐藏层输出有轻微的正则化效果（类似在隐藏层加入噪声）

BN存在的问题

当batch_size太小：统计的均值、方差估计不准确，不足以代表整体数据分布
当batch_size太大：消耗显存且训练慢
不适用于对序列长度较不固定或batch_size=1的场景，BN效果不佳

Layer Normalization(LN)

在很多任务里，batch_size很小，甚至为1；在RNN里，每一步输入大小各异， BN难以奏效。LN则解决这一问题，不依赖batch维度，在单个样本内对特征进行归一化。

LN计算公式

统计量计算维度：

对于每个样本 $n$ ，在其 所有通道 + 所有空间位置 上计算均值和方差。
即：每个样本自己内部做归一化。

数学公式：

对于第 $n$ 个样本：

$\mu_n = \frac{1}{C \cdot H \cdot W} \sum_{c,h,w} x_{n,c,h,w}$

$\sigma_n^2 = \frac{1}{C \cdot H \cdot W} \sum_{c,h,w} (x_{n,c,h,w} - \mu_n)^2$

然后进行归一化：

$\hat{x}_{n,c,h,w} = \frac{x_{n,c,h,w} - \mu_n}{\sqrt{\sigma_n^2 + \epsilon}}$

最后缩放和平移（对每个样本可以独立设置参数，也可以共享）：

$y_{n,c,h,w} = \gamma \hat{x}_{n,c,h,w} + \beta$

（注意：这里 $\gamma, \beta$ 可以是每个通道一个，也可以是整个层共享）

nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)

normalized_shape 指出在特征张量的哪些维度上做LN;
eps 为防止分母的方差估计趋近于0
elementwise_affine 指是否使用可学习的 $\gamma, \beta$

特点

不依赖batch: 适用与batch_size很小的情况，以及在序列建模（RNN、Transformer）的场景
对序列建模效果明显：由于不依赖batch_size大小和时间序列长度，在循环网络中能稳定激活分布，加快收敛。
在CNN上效果比BN差： LN统计范围相当于每个通道都被参与计算，会损失某些图像特征的局部性。

总结

BN（BatchNorm）：对一个 batch 内的每个通道（channel）单独计算均值和方差。
LN（LayerNorm）：对单个样本的所有通道、空间位置一起计算均值和方差。

BN vs LN 的关键对比

特性	BatchNorm (BN)	LayerNorm (LN)
统计维度	同一通道下，跨 batch 和空间	同一批次下，跨通道和空间
是否依赖 batch 大小	是	否
是否适合 RNN / Transformer	否	是 ✅
对 batch size 敏感	是（小 batch 影响效果）	否
是否保留样本差异性	否（batch 内共享统计）	是 ✅
应用场景	CNN 图像任务	NLP、Transformer、小 batch 场景

举个例子说明差异

假设你有一个 batch 中有 2 张图片，每张图片有 3 个通道（RGB），尺寸是 $64 \times 64$ ：

BN：对每个通道（如 R 通道）把这 2 张图的所有像素（共 $2 \times 64 \times 64$ ）拿来算均值和方差。
LN：对每一张图，把它所有的像素（共 $3 \times 64 \times 64$ ）拿来算均值和方差。

实际应用中的选择建议

模型类型	推荐使用
CNN 图像分类	BatchNorm ✅
RNN / LSTM / GRU	LayerNorm ✅
Transformer	LayerNorm ✅
小 batch size	LayerNorm 更稳定
分布变化大或 batch 不稳定	LayerNorm 更鲁棒

总结

层面	BatchNorm	LayerNorm
统计对象	每个通道（C）	每个样本（N）
统计范围	batch + 空间	通道 + 空间
是否依赖 batch	是	否
适用网络	CNN	RNN、Transformer
数学表达	均值 $\mu_c$ 、方差 $\sigma_c^2$	均值 $\mu_n$ 、方差 $\sigma_n^2$

Transformer中的LayerNorm解释

对这张图可能会做出这样的转化： $N \sim Batch_size, C \sim seq_len, H W\sim hidden_sim$

不过这样转化对BatchNorm是可以的，但对于LayerNorm就不对了。

Examples:

# NLP Example
>>> batch, sentence_length, embedding_dim = 20, 5, 10
>>> embedding = torch.randn(batch, sentence_length, embedding_dim)
>>> layer_norm = nn.LayerNorm(embedding_dim)
>>> # Activate module
>>> layer_norm(embedding)

# Image Example
>>> N, C, H, W = 20, 5, 10, 10
>>> input = torch.randn(N, C, H, W)
>>> # Normalize over the last three dimensions (i.e. the channel and spatial dimensions)
>>> layer_norm = nn.LayerNorm([C, H, W])
>>> output = layer_norm(input)

可以看到对于NLP model(Bert之后的)LayerNorm有着不同的用法，可以用下面这张图描述， LayerNorm是对每一个token的hidden_dim做归一化：

torch.nn.LayerNorm( normalized_shape, eps=1e-05, elementwise_affine=True, bias=True,device=None,dtype=None)

LN的归一化需要两个trainable参数，以及分母上的eps

手撕LayerNorm (deepseek面试题)

import torch
import torch.nn as nn

class LayerNorm(nn.Module):

    def __init__(self, featurea, eps=1e-6):
        super().__init__()
        self.gamma = nn.Parameter(torch.ones(features))
        self.beta = nn.Parameter(torch.zero(features))
        self.eps = eps


    def forward(self, x):
        mean = x.mean(-1, keepdim = True)
        std = x.std(-1, keepdim = True, unbiased = False)
        return self.gamma * (x - mean) / (std + self.eps) + self.beta

fearures = 768
layer_norm = LayerNorm(features)

x = torch.randn(10, 20, features)
normalized_x = layer_norm(x)
print(normalized_x)

如果您认为博文还不错，请帮忙点赞、收藏、关注。您的反馈是我的原动力

	原创文章
1	FFN前馈网络与激活函数技术解析：Transformer模型中的关键模块
2	Transformer掩码技术全解析：分类、原理与应用场景
3	【大模型技术】Attention注意力机制详解一
4	Transformer核心技术解析LCPO方法：精准控制推理长度的新突破
5	Transformer模型中位置编码（Positional Embedding）技术全解析(二)
6	Transformer模型中位置编码（Positional Embedding）技术全解析(一)
7	自然语言处理核心技术词嵌入（Word Embedding），从基础原理到大模型应用
8	DeepSeek-v3：基于MLA的高效kv缓存压缩与位置编码优化技术
9	【Tokenization第二章】分词算法深度解析：BPE、WordPiece与Unigram的原理、实现与优化
10	Tokenization自然语言处理中分词技术：从传统规则到现代子词粒度方法
11	[预训练]Encoder-only架构的预训练任务核心机制
12	【第一章】大模型预训练全解析：定义、数据处理、流程及多阶段训练逻辑