【剑指Offer】剪绳子问题——四种解法

题目描述：

给你一根长度为n的绳子，请把绳子剪成整数长的m段（m、n都是整数，n>1并且m>1，m<=n），每段绳子的长度记为k[1],…,k[m]。请问k[1]x…xk[m]可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

输入描述：

输入一个数n(2<=n<=60)

返回值描述：

输出答案。

示例1：

输入：8
输出：18

解题思路：

将题目描述转换成数学语言为：给定一个数n，求n=a1+a2+…+am，（m>1）在此条件下，s=a1a2…*am，s最大。
首先思考一个问题：什么样的题适合用动态规划？对于本题来说，假设我们使用暴力枚举的思路，会出现以下问题：

1. 这段绳子到底应该分为几段，才能得到最优的结果？
2. 假设已经知道要分m段，那么每段长度该如何确定？
3. …
   上面仅仅是两个最容易想到的问题。如何才能处理各种情况，并从中选出一个最优的。

方法1：暴力递归

提到暴力递归，就要想到递归三部曲：

1. 递归函数的设计和功能：backTrack(int n)，含义是：计算长度为n的数，最后分段后的最大乘积，这里不需要关心分成多少段。
2. 递归函数的终止条件：如果n<=4，显然backTrack(int n) = n，初始条件也就是我们不需要计算就能得到的。
3. 下一步递归：对于长度n，我们需要减少递归参数n，如果第一段为1，显然下一步递归为backTrack(int n-1)，如果第一段为2，则下一步递归为backTrack(int n-2)…因为要至少分2段，所以，最后一次可能的情况为最后一段为n-1，显然下一步递归为backTrack(1)，因此，每一步可能得结果为1backTrack(n-1)，2backTrack(n-2)，…，(n-1)*backTrack(1)。在n-1种情况下取一个最大值即可。这里不用关心backTrack(n-1)的值为多少，因为最终会递归到我们的终止条件，因此可以求出来。

    // 方法1, 暴力递归， 时间复杂度为O(n!)，空间复杂度为O(n)，最多分n段，每段长度为1，递归深度为n
    public static int cutRope(int target) {
        if (target == 2) {
            return 1;
        } else if (target == 3) {
            return 2;
        } else {
            return backTrack(target);
        }
    }

    private static int backTrack(int n) {
        // n<=4，表明不分割的时候，长度是最长的。
        if (n <= 4) {
            return n;
        }
        int res = 0;
        for (int i = 1; i < n; i++) {
            res += Math.max(res, i * backTrack(n - i));
        }
        return res;
    }

方法2：记忆化递归

根据方法一，假设求backTrack(7)，如下图：

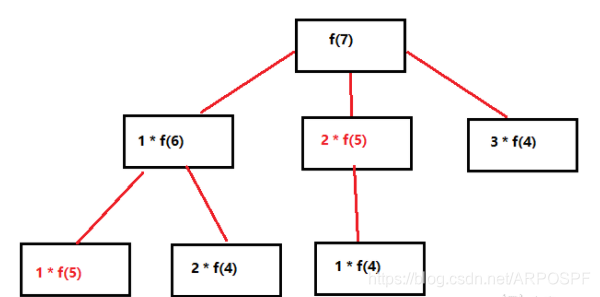
用f()替代backTrack()，可知，红色部分重复了。因此，可以开一个数组，把计算过的结果存起来。步骤如下：

• 初始化一个大小为n+1的数组，初始值为-1，也可以为-2，只要是不可能得到的值即可。
• 在方法一的代码上，记录一下。
  详细代码如下：

    // 记忆化递归，时间复杂度为O(n^2)，空间复杂度为O(n)
    static int[] mark = null;
    public static int cutRope2(int target) {
        if (target == 2) {
            return 1;
        } else if (target == 3) {
            return 2;
        }
        // 创建一个数组,初始值为0
        mark = new int[target+1];
        return backTrack2(target);
    }

    private static int backTrack2(int target) {
        if (target <= 4) {
            return target;
        }
        if (mark[target] != 0) {
            return mark[target];
        }
        int ret = 0;
        for (int i = 1; i < target; i++) {
            ret = Math.max(ret, i * backTrack2(target - i));
        }
        return mark[target] = ret;
    }

方法三：动态规划

    // 动态规划, 时间复杂度为O(n^2)，空间复杂度为O(n)
    public static int cutRope3(int target) {
        if (target == 2) {
            return 1;
        } else if (target == 3) {
            return 2;
        }
        int[] mark = new int[target + 1];
        for (int i = 1; i <= 4; i++) {
            mark[i] = i;
        }
        for (int i = 5; i <= target; i++) {
            for (int j = 1; j < i; j++) {
                mark[i] = Math.max(mark[i], j * mark[i - j]);
            }
        }
        return mark[target];
    }

思考：什么样的题目适合动态规划？一般来说，动态规划有以下几种分类：

1. 最值型动态规划，比如，求最大、最小值是多少？
2. 计数型动态规划，比如换硬币，有多少种换法？
3. 坐标型动态规划，比如在m*n矩阵求最值型，计数型，一般是二维矩阵
4. 区间型动态规划，比如在区间种求最值

方法四，数学原理

首先引入一个一般性问题：周长一定为n，这时候长length与宽width在什么情况下，达到面积s最大。
s=lengthwidth，设length=x, 则width=n/2-x。
所以s=x(n/2-x) = -x^2+nx/2。
对其求导数，得到s’ = -2x+n/2，
当s’=0，即x=n/4，
在（0，n/4）区间，s’>0，s单调递增，
在（n/4，n）区间，s’<0，s单调递减
n/4为极大值点。所以在长度x=n/4的时候，s的面积最大。此时，width=n/2-x = n/4
通过这个一般性问题，可知，截取的子段长度相等的时候，乘积最大。
对于本题来说，绳子长度为n，分成m份，那么设每份长度为x，份数为m=n/x，那么结果就是n/x个x相乘f(x) = x^(n/x)
求导，如下图

因此，问题就回到了n/3的个数上面，当n能被3整除的时候，乘积=3^(n/3)
当n除3余1的时候，这时候发现多了一个1，但是如果把前面一个3拿出来，这个时候就可以分解为22,所以乘积为3^(n/3-1)*4
当n除3余2的时候，乘积为3^(n/3)*2
代码如下：

    // 方法四，数学分析
    public static int cutRope4(int target) {
        if (target <= 0) {
            return 0;
        } else if (target == 1 || target == 2) {
            return 1;
        } else if (target == 3) {
            return 2;
        } else {
            int m = target % 3;
            switch (m) {
                case 0:
                    return (int) Math.pow(3, target / 3);
                case 1:
                    return (int) Math.pow(3, target / 3 - 1) * 4;
                case 2:
                    return (int) Math.pow(3, target / 3) * 2;
                default:
                    return 0;
            }
        }
    }