【线性代数】矩阵分解（Matrix Factorization）笔记：非负矩阵分解（实践）

已于 2023-03-13 19:28:25 修改
阅读量1.9k 收藏 15
点赞数 1
分类专栏： 高等数学基础 文章标签： 线性代数 推荐系统 非负矩阵分解 图像处理 NMF
于 2022-01-13 08:30:00 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/ARPOSPF/article/details/122441427
版权

@[TOC](非负矩阵分解(Non-negative Matrix Factorization)实践)

1. 应用概述

NMF可以应用的领域很广，源于其对事物的局部特性有很好的解释。

  • 在众多应用中，NMF能被用于发现数据库中的图像特征，便于快速自动识别应用；
  • 能够发现文档的语义相关度，用于信息自动索引和提取；
  • 能够在DNA阵列分析中识别基因等等。

其中，最有效的就是图像处理领域，是图像处理的数据降维和特征提取的一种有效方法。

1.1 特征学习

类似主成分分析（Principal Component Analysis），但是在实际工程环境当中都要比PCA效果要好，其中思想如下：

  1. 测试数据在NMF算法上学习 V t r a i n → d i c t i o n a r y W V_{train} \rightarrow dictionaryW Vtrain​→dictionaryW
  2. 利用基矩阵W去分解新的测试example V n V_n Vn​：
    v n ≈ ∑ n = 1 K h k n w k , 其中 k n > = 0 v_n\approx \sum_{n=1}^{K}h_{kn}w_k,其中k_n>=0 vn​≈n=1∑K​hkn​wk​,其中kn​>=0
  3. 把 h n h_n hn​作为example n的特征向量。
    例如，下面是对人脸进行NMF特征学习的结果：
    人脸特征学习

1.2 图像分析

NMF最成功的一类应用是在图像的分析和处理领域。图像本身包含大量的数据，计算机一般将图像的信息按照矩阵的形式进行存放，针对图像的识别、分析和处理也是在矩阵的基础上进行的。这些特点使得NMF方法能很好地与图像分析处理相结合。

  • 人们已经利用NMF算法，对卫星发回的图像进行处理，以自动辨别太空中的垃圾碎片；
  • 使用NMF算法对天文望远镜拍摄到的图像进行分析，有助于天文学家识别星体；
  • 美国还尝试在机场安装由NMF算法驱动的识别系统，根据事先输入计算机的恐怖分子的特征图像库来自动识别进出机场的可疑恐怖分子。

学术界中：
（1）NMF首次被Lee教授用于处理人脸识别。
（2）LNMF被宋教授后面提出用于提取人脸子空间，将人脸图像在特征空间上进行投影，得到投影系数作为人脸识别的特征向量，用来进行人脸识别。一定程度上提高了识别率。
（3）GNMF被杨教授提出，该算法是基于gamma分布的NMF进行构建特征子空间，采用最小距离分类对ORL人脸库部分图像进行识别。

对于人脸识别，其中以LNMF最为有效突出，比普通的NMF高效且精度高。

1.3 话题识别

文本在人类日常接触的信息中占有很大分量，为了更快更精确地从大量的文本数据中取得所需要的信息，针对文本信息处理的研究一直没有停止过。文本数据不光信息量大，而且一般是无结构的。此外，典型的文本数据通常以矩阵的形式被计算机处理，此时的数据矩阵具有高维稀疏的特征，因此，对大规模文本信息进行处理分析的另一个障碍便是如何削减原始数据的维数。NMF算法正是解决这方面难题的一种新手段。
NMF在挖掘用户所需数据和进行文本聚类研究中都有着成功的应用例子。由于NMF算法在处理文本数据方面的高效性，著名的商业数据库软件Oracle在其第10版中专门利用NMF算法来进行文本特征的提取和分类。
为什么NMF对于文本信息提取得很好呢？原因在于智能文本处理的核心问题是以一种能捕获语义或相关信息的方式来表示文本，但是传统的常用分析方法仅仅是对词进行统计，而不考虑其他的信息。而NMF不同，它往往能达到表示信息的局部之间相关关系的效果，从而获得更好的处理结果。

话题识别的Topic跟概率隐语义分析（Probabilistic Latent Semantic Analysis）相似：

  • 首先假设 V = [ v f n ] V=[v_{fn}] V=[vfn​]是一个单词-文本的矩阵， v f n v_{fn} vfn​是单词 m f m_f mf​在文本 d n d_n dn​的出现频率。
  • 假设 w f k = P ( t k ) P ( m f ∣ t k ) w_{fk}=P(t_k)P(m_f|t_k) wfk​=P(tk​)P(mf​∣tk​)和 h k n = P ( d n ∣ t k ) h_{kn}=P(d_n|t_k) hkn​=P(dn​∣tk​)，那么模型可以写成：
    [ P ( m f , d n ) ] = [ v f n ] = W H [P(m_f,d_n)]=[v_{fn}]=WH [P(mf​,dn​)]=[vfn​]=WH
    这里， w k w_k wk​可以被解释成为与数据 h k h_k hk​的主题相关度
    主题识别

1.4 语音处理

语音的自动识别一直是计算机科学家努力的方向，也是未来智能应用实现的基础技术。语音同样包含大量的数据信息，识别语音的过程也是对这些信息处理的过程。
NMF算法在这方面也为我们提供了一种新方法，在已有的应用中，NMF算法成功实现了有效的语音特征提取，并且由于NMF算法的快速性，对实现机器的实时语音识别有着促进意义。也有使用NMF方法进行音乐分析的应用。复调音乐的识别是个很困难的问题，三菱研究所和MIT(麻省理工学院)的科学家合作，利用NMF从演奏中的复调音乐中识别出各个调子，并将它们分别记录下来。实验结果表明，这种采用NMF算法的方法不光简单，而且无须基于知识库。

NMF处理声频产生局部特征数据示例：
NMF语音识别示例

1.5 时序分割（temporal segmentation）

引用隐马尔科夫模型hidden markov models HMM，可以处理时间序列的数据，例如音频视频：
NMF在时序分割中的示例
NMF可以通过阈值设置把文件序列数据分割成不同兴趣主题，下面为挖掘电影剪辑结构的一个例子：
电影示例同样基于时序分割的想法下有了这样一个语音处理项目，对很多人说的一段话进行语音特征分割，识别出每段话属于哪个人说的：
语音特征分割
不同K值下的语音分割效果

1.6 聚类

聚类最常用的方法是K-means，俗称K均值算法，NMF算法比K-means算法更优之处因为它是一种软聚类方法（也就是一个元素可以被分为多种类型，不是K-means那种非彼则此），对于有可能重复的聚类方法NMF是简单高效的。
NMF聚类

1.7 机器人控制

如何快速准确地让机器人识别周围的物体对于机器人研究具有重要的意义，因为这是机器人能迅速作出相应反应和动作的基础。机器人通过传感器获得周围环境的图像信息，这些图像信息也是以矩阵的形式存储的。已经有研究人员采用NMF算法实现了机器人对周围对象的快速识别，根据现有的研究资料显示，识别的准确率达到了80%以上。

1.8 生物医学工程和化学工程

生物医学和化学研究中，也常常需要借助计算机来分析处理试验的数据，往往一些烦杂的数据会耗费研究人员的过多精力。NMF算法也为这些数据的处理提供了一种新的高效快速的途径。

  • 科学家将NMF方法用于处理核医学中的电子发射过程的动态连续图像，有效地从这些动态图像中提取所需要的特征。
  • NMF还可以应用到遗传学和药物发现中。因为NMF的分解不出现负值，因此采用NMF分析基因DNA的分子序列可使分析结果更加可靠。
  • 同样，用NMF来选择药物成分还可以获得最有效的且负作用最小的新药物。

1.9 滤波和源分离

参考独立成分分析(Independent Component Analysis, ICA):
独立成分分析
在滤波当中，有一篇SCI使用了一个例子，即基于深度轮廓进行动作识别Action Recognition using depth silhouettes，NMF算法作为特征学习的算法。最后论文使用微软开源的Kinect的骨骼特征、PCA算法、NMF算法进行轮廓特征学习对比，发现NMF的精确率最高91%，而微软开源的骨骼特征识别度只达到78%。

NMF在电影推荐系统中的应用案例

有用户和电影两个集合。给出每个用户对部分电影的打分，希望预测该用户对其他没看过电影的打分值，这样可以根据打分值为其做出推荐。用户和电影的关系，可以用一个矩阵来表示，每一列表示用户，每一行表示电影，每个元素的值表示用户对已经看过的电影的打分。
相关的包：from sklearn.decomposition import NMF
下面简单介绍一下基于NMF的推荐算法：
数据
电影的名称，使用10个电影：

# 电影列表
item = ['Avatar', 'Unforgiven', 'Leon: The Professional', 'The Hurt Locker', 'Back to the Future',
        'The Dark Knight', 'Brave heart', 'The Notebook', 'Princess Bride', 'The Iron Giant']

用户的名称，使用15个用户：

# 用户列表
user = ['Rose', 'Lily', 'Daisy', 'Bond', 'Mask',
        'Poppy', 'Violet', 'Kong', 'Oli', 'Daffodil',
        'Camellia', 'Rust', 'Rosemary', 'Aron', 'Chen']

用户的评分矩阵：

# 用户评分矩阵
RATE_MATRIX = np.array(
    [[5, 5, 3, 0, 5, 5, 4, 3, 2, 1, 4, 1, 3, 4, 5],
     [5, 0, 4, 0, 4, 4, 3, 2, 1, 2, 4, 4, 3, 4, 0],
     [0, 3, 0, 5, 4, 5, 0, 4, 4, 5, 3, 0, 0, 0, 0],
     [5, 4, 3, 3, 5, 5, 0, 1, 1, 3, 4, 5, 0, 2, 4],
     [5, 4, 3, 3, 5, 5, 3, 3, 3, 4, 5, 0, 5, 2, 4],
     [5, 4, 2, 2, 0, 5, 3, 3, 3, 4, 4, 4, 5, 2, 5],
     [5, 4, 3, 3, 2, 0, 0, 0, 0, 0, 0, 0, 2, 1, 0],
     [5, 4, 3, 3, 2, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1],
     [5, 4, 3, 3, 1, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2],
     [5, 4, 3, 3, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1]]
)

用户和电影的NMF分解矩阵，其中nmf_model为NMF的类，user_dis为W矩阵，item_dis为H矩阵，R设置为2：

# 用户和电影的NMF分解，其中nmf_model为NMF的类，user_dis为W矩阵，item_dis为H矩阵，R设置为2:
nmf_model = NMF(n_components=2, init='nndsvd')  # 设置有2个主题
item_dis = nmf_model.fit_transform(RATE_MATRIX)
user_dis = nmf_model.components_
print('用户的主题分布：')
print(user_dis)
print('电影的主题分布：')
print(item_dis)

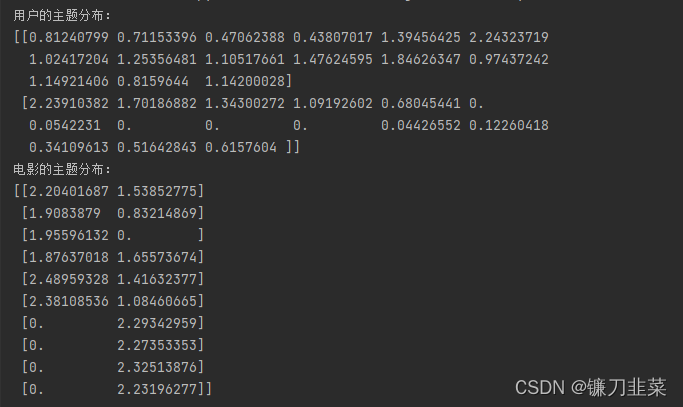矩阵分解的结果可以把电影主题分布矩阵和用户分布矩阵画出来：

# 把电影主题分布矩阵和用户分布矩阵画出来
plt1 = plt
plt1.plot(item_dis[:, 0], item_dis[:, 1], 'ro')
plt1.draw()  # 直接画出矩阵，只打了点，下面对图plt1进行一些设置

plt1.xlim((-1, 3))
plt1.ylim((-1, 3))
plt1.title(u'the distribution of items (NMF)')  # 设置图的标题

count = 1
zipitem = zip(item, item_dis)  # 把电影标题和电影的坐标联系在一起

for item in zipitem:
    item_name = item[0]
    data = item[1]
    plt1.text(data[0], data[1], item_name,
              fontproperties='SimHei',
              horizontalalignment='center',
              verticalalignment='top')
plt1.show()

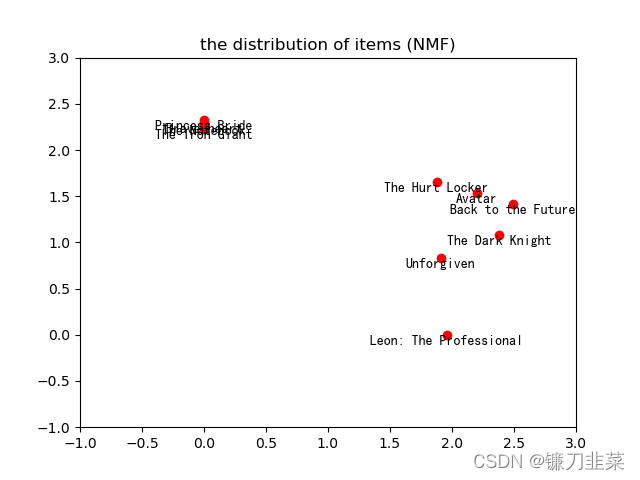
电影的主题分布
从上面的图可以看出电影主题划分出来了，使用KNN或者其他距离度量算法可以把电影分为两大类，也就是根据之前的NMF矩阵分解时候设定的n_components=2有关。后面对这个n_components的值进行解释。

再来看看用户的主题划分：

# 用户的主题划分
user_dis = user_dis.T  # 把用户分布矩阵进行转置
plt2 = plt
plt2.plot(user_dis[:, 0], user_dis[:, 1], 'ro')
plt2.xlim((-1, 3))
plt2.ylim((-1, 3))
plt2.title(u'the distribution of user (NMF)')  # 设置图的标题

zip_user = zip(user, user_dis)  # 把电影标题和电影的坐标联系在一起
for user in zip_user:
    user_name = user[0]
    data = user[1]
    plt2.text(data[0], data[1], user_name,
              fontproperties='SimHei',
              horizontalalignment='center',
              verticalalignment='top')
# 直接画出矩阵，只打了点，下面对图plt2进行一些设置
plt2.show()

用户的主题分布
从上图中可以看出，用户’Rose’、’Lily‘，’Daisy‘，’Bond‘具有类似的距离度量相似度，其余11个用户具有类似的距离度量相似度。
推荐
对于NMF的推荐很简单，具体过程如下：

  1. 求出用户没有评分的电影，因为在numpy的矩阵里面保留小数位8位，判断是否为零使用1e-8（后续可以方便调节参数），当然，如果没有那么严谨的话可以用= 0。
  2. 求出过滤评分的新矩阵，使用NMF分解的用户特征矩阵和电影特征矩阵点乘。
  3. 求出要求得用户没有评分得电影列表，并根据大小排列，就是最后要推荐给用户得电影ID了。
filter_matrix = RATE_MATRIX < 1e-8
rec_mat = np.dot(item_dis, user_dis)
print('重建矩阵，并过滤掉已经评分的物品：')
rec_filter_mat = (filter_matrix * rec_mat).T
print(rec_filter_mat)

# 需要进行推荐的用户
rec_user = 'Camellia'
# 推荐用户ID
rec_userid = user.index(rec_user)
# 推荐用户的电影列表
rec_list = rec_filter_mat[rec_userid, :]

print('推荐用户的电影：')
print(np.nonzero(rec_list))
执行结果如下：
重建矩阵，并过滤掉已经评分的物品：
[[0.         0.         1.5890386  0.         0.         0.
  0.         0.         0.         0.        ]
 [0.         2.7740907  0.         0.         0.         0.
  0.         0.         0.         0.        ]
 [0.         0.         0.92052211 0.         0.         0.
  0.         0.         0.         0.        ]
 [2.64547255 1.74465262 0.         0.         0.         0.
  0.         0.         0.         0.        ]
 [0.         0.         0.         0.         0.         4.0586019
  0.         0.         0.         0.        ]
 [0.         0.         0.         0.         0.         0.
  0.         0.         0.         0.        ]
 [0.         0.         2.0032409  2.01150506 0.         0.
  0.12435687 0.12327804 0.12607624 0.12102394]
 [0.         0.         0.         0.         0.         0.
  0.         0.         0.         0.        ]
 [0.         0.         0.         0.         0.         0.
  0.         0.         0.         0.        ]
 [0.         0.         0.         0.         0.         0.
  0.         0.         0.         0.        ]
 [0.         0.         0.         0.         0.         0.
  0.10151985 0.10063914 0.10292348 0.09879899]
 [0.         0.         1.90583476 0.         2.59943825 0.
  0.28118406 0.27874473 0.28507174 0.27364798]
 [0.         0.         2.24781825 2.72111639 0.         0.
  0.         0.         0.79309584 0.76131387]
 [0.         0.         1.59599481 0.         0.         0.
  0.         1.17411736 0.         0.        ]
 [0.         2.69178372 2.23370837 0.         0.         0.
  1.41220313 0.         0.         0.        ]]
推荐用户的电影：
(array([6, 7, 8, 9], dtype=int64),)

通过上面结果可以看出来，推荐给用户’Camellia’的电影可以有’The Dark Knight’, ‘Brave heart’, ‘The Notebook’, ‘Princess Bride’。
误差
查看分解后的误差：

a = NMF(n_components=2)  # 设有2个主题
W = a.fit_transform(RATE_MATRIX)
H = a.components_
print(a.reconstruction_err_)

b = NMF(n_components=3)  # 设有3个主题
W = b.fit_transform(RATE_MATRIX)
H = b.components_
print(b.reconstruction_err_)

c = NMF(n_components=4)  # 设有4个主题
W = c.fit_transform(RATE_MATRIX)
H = c.components_
print(c.reconstruction_err_)

d = NMF(n_components=5)  # 设有5个主题
W = d.fit_transform(RATE_MATRIX)
H = d.components_
print(d.reconstruction_err_)

上面的误差分别是

13.823891101850649
10.478754611794432
8.223787135382624
6.120880939704367

在矩阵分解当中忍受误差是有必要的，但是对于误差的多少呢，我们认为通过NMF计算出来的误差不用太着迷，更要的是看你对于主题的设置分为多少个。很明显的是主题越多，越接近原始的矩阵误差越少，所以先确定好业务的需求，然后定义应该聚类的主题个数。

总结

以上虽使用NMF实现了推荐算法，但是根据Netfix的CTO所说，NMF他们很少用来做推荐，用得更多的是SVD。对于矩阵分解的推荐算法常用的有SVD、ALS、NMF。对于哪种更好和对于文本推荐系统来说很重要的一点是搞清楚各种方法的内在含义。
另外，补充SVD、ALS、NMF三种算法在实际工程应用中的区别。

  • 对于一些明确的数据使用SVD（例如用户对item的评分）
  • 对于隐含的数据使用ALS（例如purchase history购买历史，watching habits浏览兴趣 and browsing activity活跃记录等）
  • NMF用于聚类，对聚类的结果进行特征提取。

在上面的实践当中就是使用了聚类的方式对不同的用户和物品进行特征提取，特征可以看成是推荐的相似度，所以可以用来作为推荐算法。但是并不推荐这样做，因为和SVD对比，NMF的精确率和召回率并不显著。

参考资料

  1. https://blog.csdn.net/qq_26225295/article/details/51211529
  2. https://blog.csdn.net/qq_26225295/article/details/51165858
[论文笔记] 概率矩阵分解：Probabilistic Matrix Factorization
心宝的博客
11-12 1862
Abstract 许多现有的协作过滤方法都不能处理非常大的数据,也不容易处理评分很少的用户。 在本文中，我们提出了概率矩阵分解(PMF)模型，该模型 与观测数据的数量成线性关系（为什么线性），更重要的是，在大型、稀疏和非常不平衡的Netflix数据集上表现良好。 我们进一步扩展了PMF模型，以包括一个自适应的先验模型参数，并展示了如何自动控制模型容量。 最后，我们介绍了PMF模型的一个受限制的版本，该模型基于这样一个假设:对类似电影集进行评级的用户可能有类似的偏好。 此模型能够对评分很少的...
矩阵分解笔记（Notes on Matrix Factorization）
热门推荐
mingo_敏
07-04 1万+
本博文主要讨论 基本矩阵（Basic MF），非负矩阵（Non-negative MF）和正交非负矩阵（Orthogonal non-negative MF）三种常见的矩阵分解方法。并分别推导了它们的更新规则，收敛性，以及它们的应用。 本文地址：http://blog.csdn.net/shanglianlm/article/details/46755239
机器学习 -- Matrix Factorization
01-30
Matrix Factorization More about Matrix Factorization Matrix Factorization for Topic analysis
Matrix Factorization
绿箭侠
07-31 178
Matrix Factorization ①linearNetwork Hypothesis 机器学习的作用就是要从一堆数据中学习到学习到某种能力，然后用这种skill来预测未来的结果。比如一个电影推荐的例子，我们手上有很多的电影数据，现在就需要训练一个机器学习的模型来使得这个模型可以预测一个新来的用户会喜欢什么电影，然后推荐过去。或者是对用户没有看过的电...
Matrix Factorization（矩阵分解）
王利锋Fandy
11-30 3298
http://www.quuxlabs.com/blog/2010/09/matrix-factorization-a-simple-tutorial-and-implementation-in-python/ http://langvillea.people.cofc.edu/NISS-NMF.pdf?referrer=webcluster& http://www.intellige
用于社区检测的类深度自动编码器非负矩阵分解——中南大学彭汪祺--论文研读笔记11
08-04
【用于社区检测的类深度自动编码器非负矩阵分解】这篇论文主要探讨的是如何利用深度学习的方法改进非负矩阵分解（NMF）技术，以更好地应用于社区检测。社区检测是网络分析的重要部分，旨在识别网络中具有紧密内部...
非负矩阵分解matlab代码-pyh2nmf:分层rank-2非负矩阵分解的python端口
06-12
非负矩阵分解的 python 端口。 2014年 原始matlab代码在这里： 论文：参见 N. Gillis、D. Kuang 和 H. Park，“使用 Rank-Two Nonnegative Matrix Factorization 的高光谱图像分层聚类”，IEEE Trans。 地球科学与...
MATRIX FACTORIZATION TECHNIQUES FOR RECOMMENDER SYSTEMS论文笔记；推荐系统中的矩阵分解（MF）
qq_37959202的博客
04-08 745
MATRIX FACTORIZATION TECHNIQUES FOR RECOMMENDER SYSTEMS Yehuda Koren, Yahoo Research Robert Bell and Chris Volinsky, AT&T Labs—Research 在看到MF的时候不太清楚，这个具体是个啥，说是根据SVD进行矩阵的分解，在看了论文后有了一个大体的了解。现在先大概的介...
Probabilistic Matrix Factorization
10-25
最经典和最基础的概率矩阵分解算法，广泛运用于推荐系统
GNMF_GNMF_非负矩阵分解_梯度下降_
09-29
一种梯度下降来迭代优化的矩阵分解的方法，并添加了迭代因子加速
非负矩阵分解—NMF应用实例
theagao&leozhang
09-18 4834
NMF应用示例 对于一个混合语音，如鼓点和管乐器混合的单通道声音，可以利用非负矩阵进行分解，实现语音信号的分离。 思路：  语音的时频分析，得到的语谱图是一个二维数据矩阵，其中鼓点、管乐器的概率分布不同，利用NMF可以实现信号的分离。 对应代码（NMF调用上面任何一个都可以）： % Read in audio file [x0 fs] = audioread('test_audio.w...
Matrix factorization
ER
08-18 738
以为降维是很多认知(广义的分类)问题的最终目的，现流行的推荐系统大多数都在做降维工作，Matrix factorization是足够简洁华丽的降维方法 Information-theoretical label embeddings for large-scale image classification
matrix factorization
guo_tt的博客
02-26 790
matrix factorization
数据挖掘实验--非负矩阵分解
萝卜丝儿皮尔
11-13 562
注：活跃集方法速度比较慢，尚且没验证上述活跃集算法的MATLAB程序是否可执行????
机器学习技法 之 矩阵分解（Matrix Factorization）
士杰的博客
05-02 2062
推荐系统 这里用推荐系统的应用实例引出矩阵分解： 现在有一个电影评分预测问题，那么数据集的组成为： {(x~n=(n),yn=rnm): user n rated movie m} \left\{ \left( \tilde { \mathbf { x } } _ { n } = ( n ) , y _ { n } = r _ { n m } \r...
【机器学习基础04】矩阵分解（Matrix Factorization）
chadlee
01-21 509
完成了机器学习基础的学习，笔者还分享了基于矩阵分解的CTR模型供参考 矩阵分解进阶：FM、FFM 矩阵分解与深度学习：DeepFM、xDeepFM 矩阵分解与特征交叉：Wide & Deep、Deep & Cross Network 矩阵分解（Matrix Factorization） 对于数据集 D\mathcal DD ，该假设函数的基于平方误差的误差测量为： Ein ({wm},{vn})=1∑m=1M∣Dm∣∑user n rated mov
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

镰刀韭菜

看在我不断努力的份上，支持我吧

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值