矩阵论极简笔记（2）:列空间、正交补、零空间、行空间

本篇讲解线性代数的4个基本空间

Vector space, subspace, linear space 是同一个东东

子空间（subspace）可以想象成一个超平面，根据线性空间的定义，0元素必须在超平面上才是子空间。

上式不是子空间。因为

直线当然是平面的子空间，直线、平面当然是三维空间的子空间。

例1

频域是有限带宽的复数空间的信号x是子空间：

子空间的直和direct sum

Span你理解正确了吗？

span{S} = {set of all possible linear combinations of vectors in S}

例2

the set

虽然向量集合是一条直线，但是张成的子空间是平面。

例3

所以，集合并集union不等于集合加和sum。该例并集是一个点和y轴，sum为过（1，0）平行y轴的一条直线。

Two subspaces are called disjoint when the only vector common to both is 0. When two subspaces S and T are disjoint, then their sum is called a direct sum (denoted S ⊕ T ).

代数补algebraic complements

或正交补(orthogonal complement)

可见，代数补并不是集合补集。

T和S是R2的代数补，T和Q也是R2的代数补，

因为，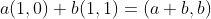

正交补(orthogonal complement)

正交补定义为：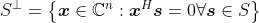

例4

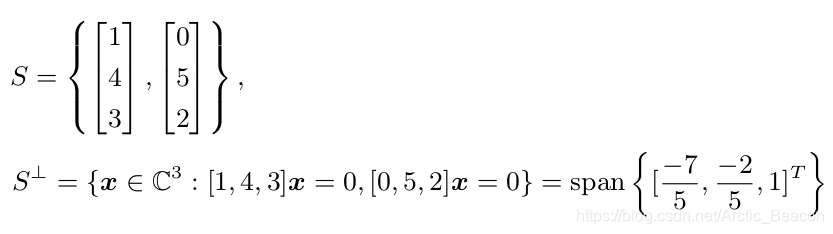
证明：S是子空间，那么其正交补也是子空间。

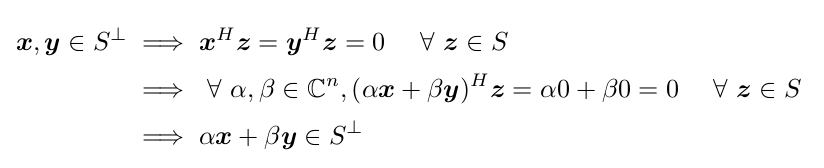
以上，即得到一个重要的向量分解思想：向量+其正交补，且唯一。

上式证明：

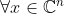,P是子空间S的投影算子

正交补的重要性质

根据定义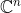，的正交补只有0元素。

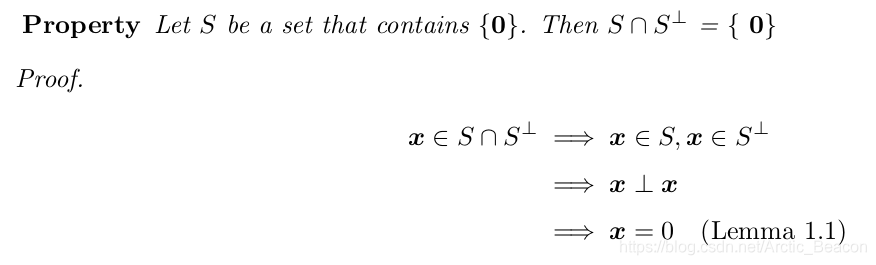
列空间Range space: Subspaces Associated with Linear Maps

例5 

固定FIR滤波器响应, h, x为复数空间任意值，所有可能的信号输出y是子空间：

所以y属于R(H)，那就存在一个信号x，卷积得到y。这在反卷积求x具有应用意义。

列空间还有一个典型应用就方程组求解，对于Ax=b，显然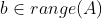，方程组有解

上述定理当然须m ≤ n，即方程个数不能多于未知数，否则可能无解也可能有解；且须行满秩，否则会出现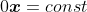，无解。

A是行满秩，一定有解，包括无穷多解。只有列大于等于行才可能行满秩。

A是列满秩序，无解或有唯一解。只有行大于等于列可能列满秩。

行满秩，且行比列少，解系肯定有自由变量。无穷多解。

列满秩，存在唯一映射  ，且b不可能为0，即A的零空间N（A）={0}

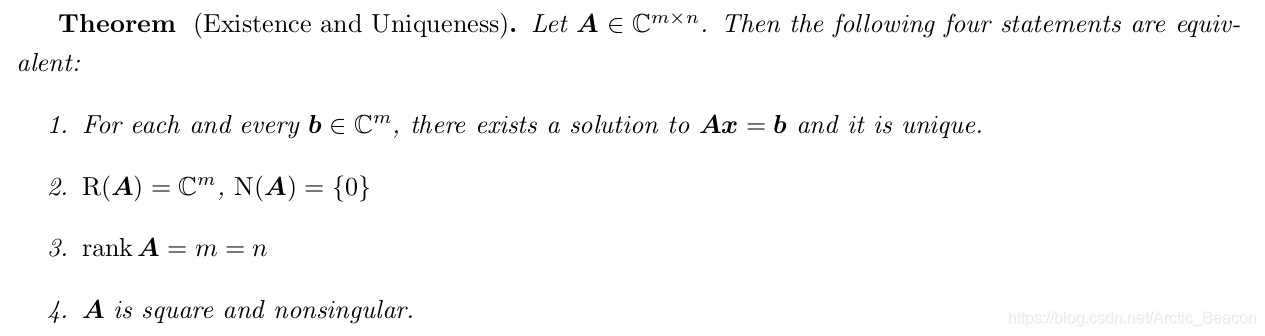
对于Ax=b的解结构可称之为仿射子空间

投影

投影的重要性质

1. 投影唯一，矩阵P是投影算子，Px是投影（垂足）
2. 子空间S垂足的投影还是本身。
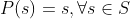
3. 子空间S的投影算子P是一个矩阵，在正交补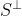的投影=0。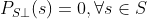
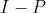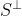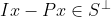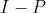4. 子空间S的投影算子P，那么是正交补的投影算子，因为,所以是正交补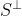的投影算子。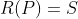
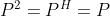
5. 
6. 

4个基本子空间

复数空间可以分解为矩阵A的列空间+矩阵A的列空间的正交补，而矩阵A的列空间的正交补=矩阵A转置的零空间。

附录  灵魂问答

矩阵乘法怎么用希格码求和表达？

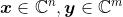
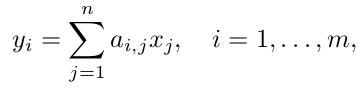
矩阵转置怎么用元素表示？

以及