对 Transformer 中位置编码 Position Encoding 的理解

LegendBIT

已于 2024-03-26 23:21:27 修改

阅读量2.1k

点赞数 33

分类专栏：深度学习--基础知识文章标签： transformer 深度学习人工智能

于 2024-03-26 22:12:25 首次发布

本文链接：https://blog.csdn.net/BIT_Legend/article/details/137042032

版权

深度学习--基础知识专栏收录该内容

5 篇文章

订阅专栏

文章详细探讨了Transformer中使用位置编码的不同方法，包括Sinusoidal位置编码、RoPE（旋转位置编码）和ALiBi（注意力带有线性偏置的输入长度外推），强调了它们在捕捉序列顺序信息和可解释性方面的特点，以及在大语言模型中的可延长性需求。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

什么是位置编码 Position Encoding

一、将绝对位置编码加在 Transformer 的输入端 (Sinusoidal 位置编码或可学习位置编码)

二、将绝对位置编码乘在 q k v (RoPE 位置编码)

三、将相对位置编码加在注意力权重 (ALiBi 位置编码)

什么是位置编码 Position Encoding

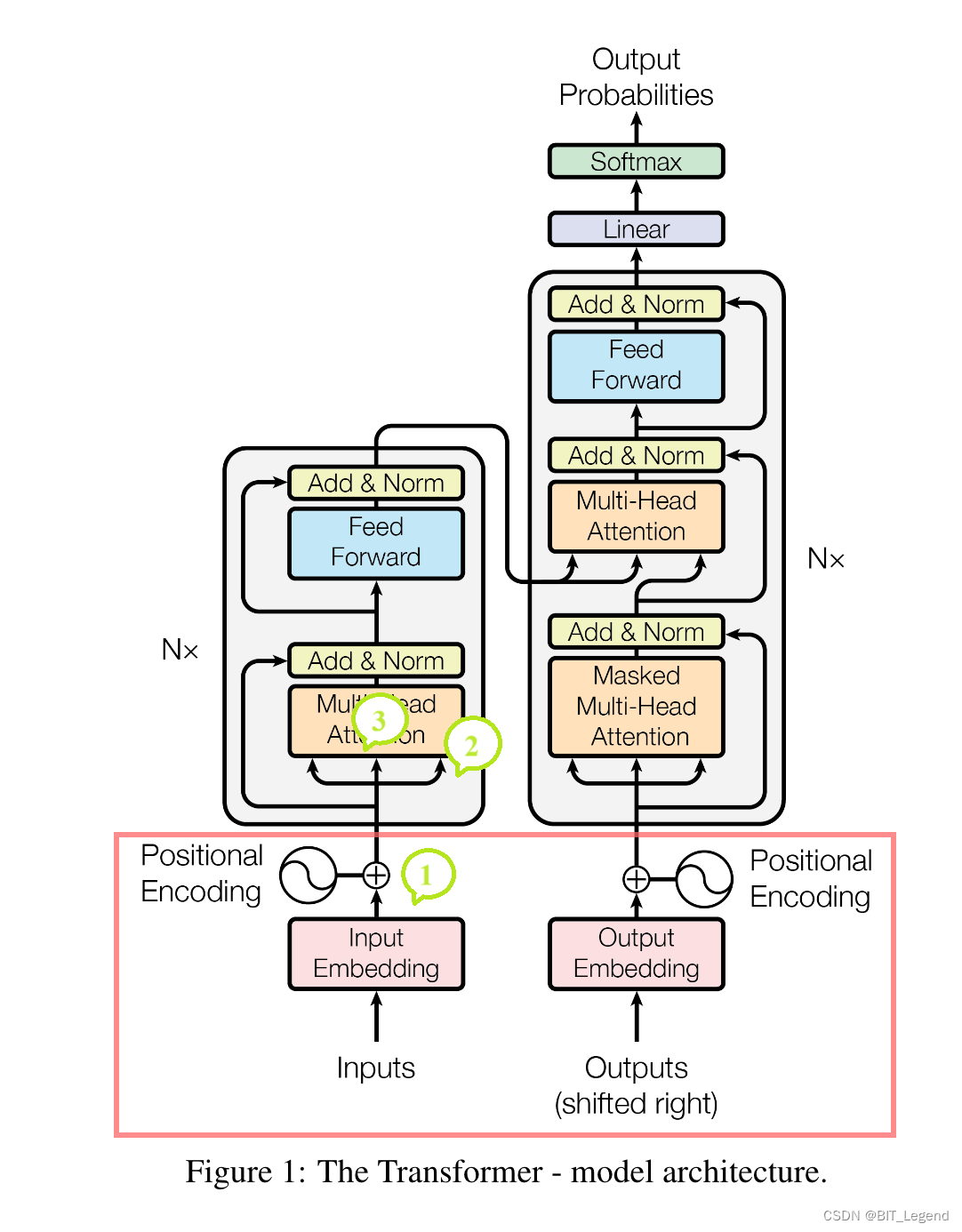
Transformer 的本质是一种全局注意力机制，它将输入序列中任意两个点之间的距离变为 1，可以实现长时或长距离的注意力机制。但这样带来的问题是，输入序列丧失了顺序信息，而对 NLP 来说输入字符的顺序是十分重要的，所以就需要位置编码 Position Encoding 来帮助 Transformer 感知输入序列的顺序信息。关于 Transformer 的基本原理和计算过程可以参考。基于位置编码 Position Encoding 的加载位置，可以将位置编码 Postion Encoding 分为：

如上图位置 1，将绝对位置编码加在 Transformer 的输入端，典型代表是 Sinusoidal 位置编码和可学习位置编码；
如上图位置 2，将绝对位置编码乘在 q k v ，典型代表是 RoPE 位置编码；
如上图位置 3，将相对位置编码加在注意力权重 $q^{T}k$ ，典型代表是 ALiBi 位置编码。

绝对位置编码指的是可以施加在某向量上的位置编码向量或者位置编码矩阵，在位置编码向量或者位置编码矩阵中包含位置或序列信息。相对位置编码并不是具体的位置编码向量或者位置编码矩阵，而是直接把基于两个位置的相对距离计算的权重直接加在注意力系数上。

一般而言，对于绝对位置编码的要求是：

位置编码中的数值必须是有界的，不能类似于 1 .. n 的形式，这样不利于模型训练
不同位置编码之间可以通过线性变换进行转换，且线性变换矩阵仅仅与两位置之间的相对位置有关，这样便于模型的学习
不同位置编码之间的内积需要具有衰减特性，以体现距离近的位置相关度更强，距离远的位置相关度更弱

相对位置编码不存在具体数值，所以对其要求仅仅是：

不同位置之间的编码值仅仅与两位置之间的相对距离有关，且这个编码值需要具有衰减特性，以体现距离近的位置相关度更强，距离远的位置相关度更弱

位置编码的原理是什么，在 Transfomer 计算中如何起作用，这个很难说清楚，深度学习本就具有不可解释性，更多的是通过大量实验尝试出来的结果。但是从可解释性上来说，从1 到 2 到 3，可解释性逐步变强。

在大语言模型中，对位置编码 Position Encoding 有一个新的要求，就是可延长性。所谓可延长性指的是训练时模型只看到了 1 .. n 位置的位置编码，但测试时可能出现 n+1 或者更远位置的位置编码。想要让位置编码具有可延长性，就需要让模型仅仅学习位置编码的相对特征而不是绝对特征，即任意两个位置，只要距离相同，那对加权系数的影响应该相同，从 1 到 2 到 3，理论上位置编码的可延长性逐步增强。但当前在大语言模型中，方案 2 的应用更广泛。

但实际上，深度学习模型是不可解释的，是没有严格理论逻辑的，很多都是总结的规律而已，在实际应用中可能需要多次尝试，选取最佳方案。

一、将绝对位置编码加在 Transformer 的输入端 (Sinusoidal 位置编码或可学习位置编码)

对于绝对位置编码最容易想到的就是二进制编码，假设输入特征的维度是 3，那二进制编码如下图所示：

可以获得 8 个位置的绝对位置编码，但此种编码方式不满足绝对位置编码要求中的后两点，所以实际使用效果并不好。

当前最常用的绝对位置编码方式为 Sinusoidal 编码，它满足所有要求。位置 t 处的绝对位置编码为：

其中， $\omega _{k}=\frac{1}{10000^{\frac{2k}{d}}}$ ，d 是特征长度，k 取值范围是 1 ~ d/2。可以看出来上面位置编码每两个为一组，对于长度为 d 的位置编码，总共包含 d/2 组 sin 与 cos 的组合，每一组组合中的角速度是相同的，从上往下角速度逐步变小，最后一组组合的角速度为 1/10000，足以保证有 2*3.1415*10000 个绝对位置编码而不重复。可以把这个位置编码想象成一个包含 d/2 个指针的时钟，一个 sin 与 cos 组合构成一根指针，总共 d/2 根指针，这些指针的旋转角速度，从上往下逐步减小，就像从秒针到时针变化一样，也像十进制编码一样从低位到高位变化速度逐步减慢，在最下面的指针完成一圈旋转之前，不会出现重复的位置编码。

Sinusoidal 位置编码的使用方式是直接加在经过 Input Embedding 后的特征向量上，很多人会有疑问，为何选择相加而不是 concat，感觉相加会存在信息损失。但如上图所示，当 Q 与 A 完全相等时，相加和 concat 的效果完全一样。当 Q 与 A 不相等时，如果 head 只有一个，那通过调整 p 的值也可以做到完全等效。当 Q 与 A 不相等时，且 head 有多个时，相加与 concat 相比只是损失了很小一部分自由度，但是却换来了计算速度和内存使用上的优势，且很多时候过多的自由度有可能会增加训练难度、增加过拟合风险和降低模型性能，所以这里一般使用相加而不是 concat。由于深度学习模型本质上其实就是线性特征提取加非线性激活函数，所以最终 q 还是求和得到的，即使相加与 concat 不是完全等效，但最终还是归于求和操作。

接下来分析一下绝对位置编码的原理，绝对位置编码是通过对 q 和 k 施加影响，进而影响 $q^{T}k$ 这个注意力权重系数。所以如上图所示，当把绝对位置编码加在 Input Embedding 后的特征向量上，那对 $q^{T}k$ 的影响很复杂，难以分析 p 对这个注意力权重系数造成了什么影响，所以可解释性很低。

在参考中，通过实际计算证明 Sinusoidal 是存在衰减特性的。从参考中可以知道，不同位置的位置编码可以通过一个仅与两位置相对距离相关的旋转矩阵线性变换得到，且不同位置编码的内积满足衰减性，所以 Sinusoidal 位置编码满足所有 3 点要求。

但 Sinusoidal 位置编码的可延长性并不好，推测原因可能是如上公式所示，当 x1 x2 Q K 固定时， $q^{T}k$ 的结果并不仅仅取决于 p1 和 p2 的相对位置，还取决于其绝对位置。

很多应用下，直接让绝对位置编码变为可学习的参数，虽然效果也很好，但这个的可解释性就更低了。

二、将绝对位置编码乘在 q k v (RoPE 位置编码)

RoPE (Rotary Position Embedding) 旋转式位置编码是通过将一个向量旋转某个角度，为其赋予位置信息。它本质上与 Sinusoidal 位置编码是一样的，都是通过旋转角度来赋予特征向量以位置信息。有时也称 RoPE 为相对位置编码。

还是以从上到下的指针分布举例，对于 Sinusoidal 位置编码，其生成位置编码向量的过程就是，首先让所有指针都从 0 位置开始旋转，每个编码的序列位置对应一个旋转时长，只是从上到下的指针旋转速度不一样，越往下速度越慢。对于 RoPE，它并不会真的生成一个位置编码向量，而是生成一个位置编码旋转矩阵，并作用于 q 和 k 上，q 和 k 也是从上往下，每两个值构成一个指针，长度为 d 的 q 总共包含 d/2 个指针，且 q 确定后，每个指针的指向也就确定好了，且一般肯定不是起于 0 位置，这里与 Sinusoidal 不同。然后基于编码的序列位置对 q 的所有指针旋转一个时间长度，从上到下的旋转角速度从大到小，以实现对 q 的位置编码。这个旋转过程就是由位置编码旋转矩阵实现的，位置编码旋转矩阵的形式为：

其中，i 表示维度分组索引， $\theta _{i}=10000^{\frac{-2i}{d}}$ 表示的是旋转角速度，m 是编码的序列位置，也可以说是旋转时间长度。

接下来分析一下 RoPE 编码的原理，它是直接作用在 q 和 k 之上，从而影响 $q^{T}k$ 这个注意力权重系数。所以如上图所示，当把旋转位置编码矩阵乘在 q 和 k 上时，对 $q^{T}k$ 的影响也很复杂，在参考中存在对这个式子的拆解分析，相比 Sinusoidal 要简单点，所以可解释性稍微好点。

在参考中，通过实际计算证明 RoPE 是存在衰减特性的。RoPE 的旋转位置矩阵显然可以通过线性变换进行变换。所以 RoPE 满足绝对位置编码的 3 个要求。

RoPE 位置编码的可延长性很好，推测原因可能是如上公式所示，当 x1 x2 固定时， $q^{T}k$ 的结果仅仅取决于 x1 和 x2 的相对位置，模型最终计算结果仅仅与相对位置有关，故具有理论上的可延长性。

三、将相对位置编码加在注意力权重 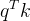$q^{T}k$ (ALiBi 位置编码)

ALiBi (Attention with Linear Biases Enables Input Length Extrapolation)是相对位置编码，它的原理很简单，它直接作用于注意力权重 $q^{T}k$ 之上，AliBi 就是一个如下图所示的矩阵，可以直接与 $q^{T}k$ 求和。观察这个矩阵可以发现，这是一个相对距离矩阵，只要相对位置越近则衰减越小，且衰减的幅度与绝对位置无关。所以，ALiBi 既满足相对位置编码的一个要求，也具有很好的可延长性。ALiBi 的可解释性也非常好。