版权声明:本文为博主原创文章,转载请附上博文链接!
三、掀开EKF2的神秘面纱
EKF2是EKF算法在ardupilot上的代码实现。读到这里你也许已经忘了,EKF的5大公式(虽然下面是7个公式,但你将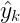
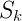

状态转移模型和观测模型如下:
上面这几个公式,一定要烂熟于心,下面给出EKF2使用的公式(这个几个公式是我读了GenerateNavFilterEquations.m后总结出来的):
预测
预测状态估计:
预测协方差估计:
更新
创新或计算剩余
创新(或残差)协方差
接近最优的卡尔曼增益
更新状态估计 
更新的协方差估计 
状态转移矩阵和观测矩阵被定义为以下雅克比行列式:


矩阵 和
和被定义为以下雅克比行列式:


状态转移模型和观测模型如下:


上述的13个公式,就是EKF2所使用的公式,这13个公式在维基百科中有个学名叫非加性噪声公式和方程。单看这个学名有点懵,实际他们的区别就在于状态转移模型和观测模型中噪声所在的位置。因为噪声不能直接加在 和
和 后面,只能写成
后面,只能写成 和
和 的形式,所以叫做非加性噪声公式和方程。实际上
的形式,所以叫做非加性噪声公式和方程。实际上 和
和 是方程
是方程 和
和 的一种更加通用的表示方式。由于状态转移模型和观测模型的不同,EKF2锁使用的方程中,多出了矩阵
的一种更加通用的表示方式。由于状态转移模型和观测模型的不同,EKF2锁使用的方程中,多出了矩阵 和
和 。这两个叫什么我目前也不清楚。
。这两个叫什么我目前也不清楚。
在EKF2实际的应用中,过程噪声矩阵 中有些元素是非加性的,有些不是。观测噪声矩阵
中有些元素是非加性的,有些不是。观测噪声矩阵 中的元素都是加性的,所以上面的公式可以化简为如下公式:
中的元素都是加性的,所以上面的公式可以化简为如下公式:
预测
预测状态估计:
预测协方差估计:
更新
创新或计算剩余
创新(或残差)协方差
接近最优的卡尔曼增益
更新状态估计 
更新的协方差估计 
状态转移矩阵和观测矩阵被定义为以下雅克比行列式:


矩阵 被定义为以下雅克比行列式:
被定义为以下雅克比行列式:

状态转移模型和观测模型如下:


过程噪声矩阵 中有些元素是非加性的,有些是加性的,所以在EKF2的实现中,预测协方差估计方程中的协方差矩阵
中有些元素是非加性的,有些是加性的,所以在EKF2的实现中,预测协方差估计方程中的协方差矩阵 有些元素加的是
有些元素加的是 有些加的是
有些加的是 。
。












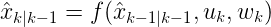
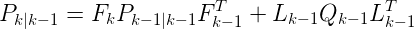

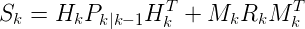
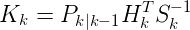
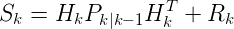

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








