超图hypergraph

   最近看了篇Paper，里面出现了一个超图（Hypergraph）的概念，论文里的解释不是很清楚，所以不是很懂，这里研究下子。

      超图（Hypergraph）是什么

      简单的来说，对于我们熟悉的图而言，它的一个边（edge）只能和两个顶点连接；而对于超图来讲，人们定义它的边（这里叫超边，hyperedge）可以和任意个数的顶点连接。一个图和超图的示意图如下所示：

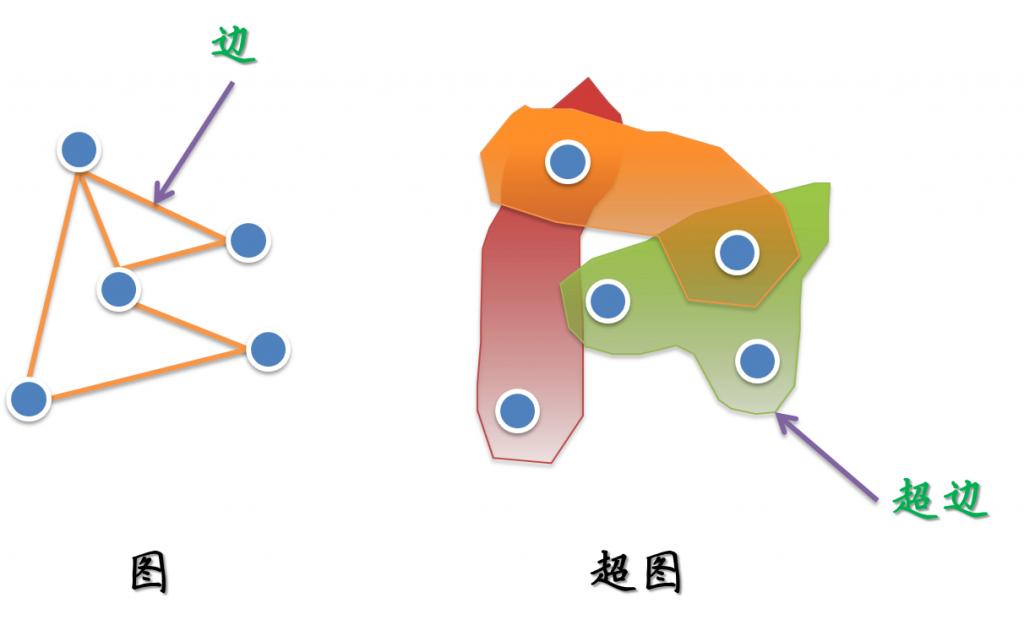
      而对于超图的一个严格的数学定义，维基百科上是这样写的：

      In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = (X,E) where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links.

      k-均匀超图（k-uniform hypergraph）

      对于超图而言，还有一个k-均匀超图的概念（k-uniform hypergraph）。它指超图的每个边连接的顶点个数都是相同的，即为个数k。所以2-均匀超图就是我们传统意义上的图，3-均匀超图就是一个三元组的集合，以此类推。

      While graph edges are pairs of nodes, hyperedges are arbitrary sets of nodes, and can therefore contain an arbitrary number of nodes. However, it is often useful to study hypergraphs where all hyperedges have the same cardinality: a k-uniform hypergraph is a hypergraph such that all its hyperedges have size k. (In other words, it is a collection of sets of size k.) So a 2-uniform hypergraph is a graph, a 3-uniform hypergraph is a collection of triples, and so on.