参考:马同学马同学提供线性代数,微积分,概率论与数理统计,机器学习等知识讲解 https://www.matongxue.com/madocs/243/
https://www.matongxue.com/madocs/243/
在我学习微积分的过程中,我对导数的认知经历了三次变化:(1)导数是变化率、是切线的斜率、是速度、是加速度;(2)导数是用来找到“线性近似”的数学工具;(3)导数是线性变换。
我认为第一种认知比较片面,在多元函数的情况下甚至是错误的。第二种认知更接近微积分的本质,第三种认知是为了实现第二种认知发展出来的。因为种种原因,我们的学习都是从第一种认知开始的。我会在本文分别介绍一下这三种认知。最后会通过第三种认知回答“多元微积分中,可微函数的切线为什么会共面(此平面即切平面)?”
1、导数是变化率、是切线的斜率、是速度、是加速度
微积分的发明人之一是牛顿,牛顿主要还是研究物理为主,微积分不过是他发明出来研究物理的一个数学工具(大师就是这么厉害)。因为牛顿研究物理的缘故,所以牛顿用变化率的方式引入了导数(牛顿称之为“流数”)。在物理里面变化率还是很自然的概念,比如为了求瞬时速度:

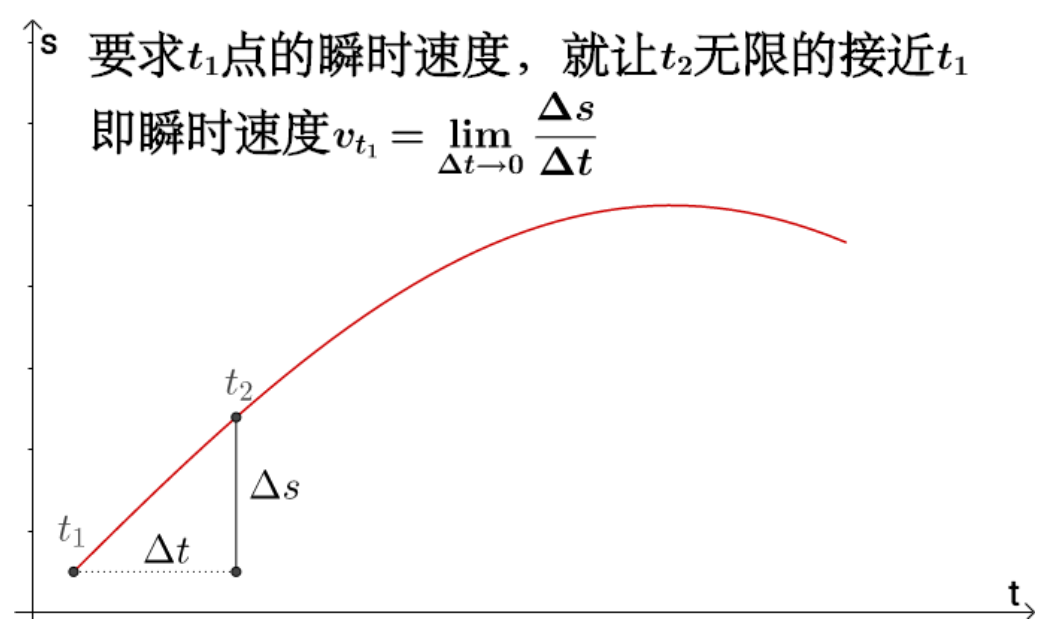
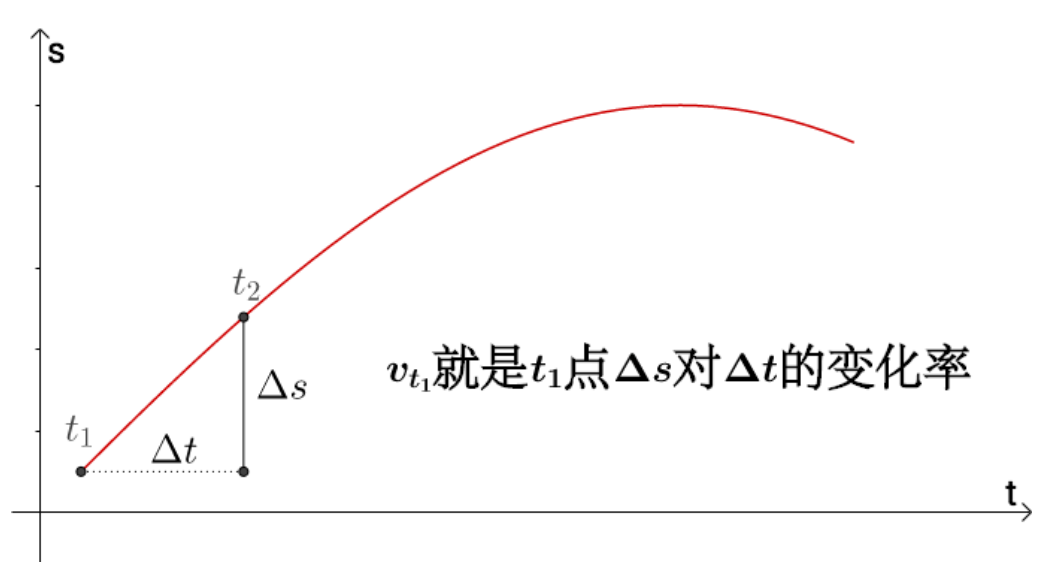
同理,求加速度的话就是求速度对于时间的变化率,这里就不赘述了。学习物理的一般习惯把导数看作变化率。还可以顺便得到了切线的斜率:
 我们一般是上面这样的学习过程,所以我们认为,导数是曲线的变化率、是瞬时速度、是加速度,还可以是切线的斜率。
我们一般是上面这样的学习过程,所以我们认为,导数是曲线的变化率、是瞬时速度、是加速度,还可以是切线的斜率。
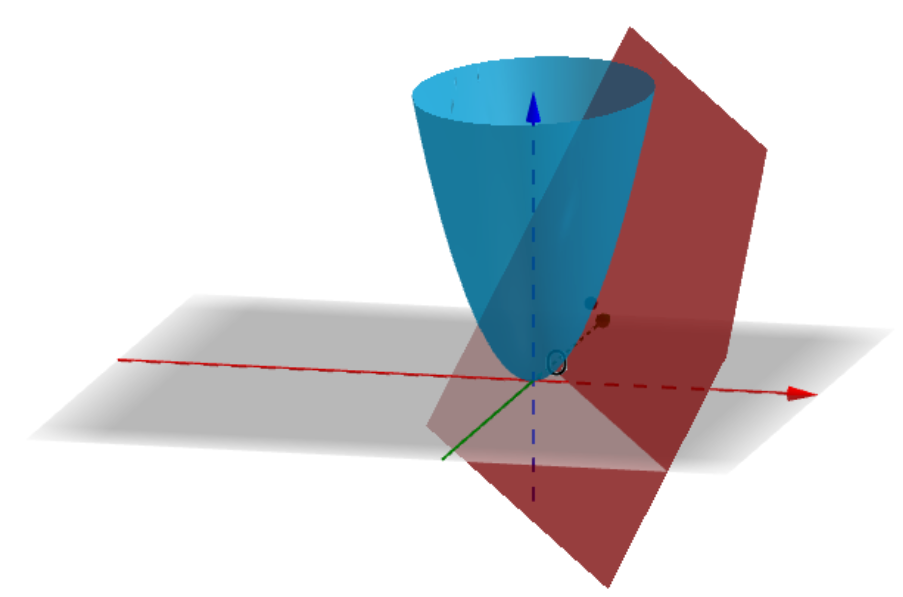
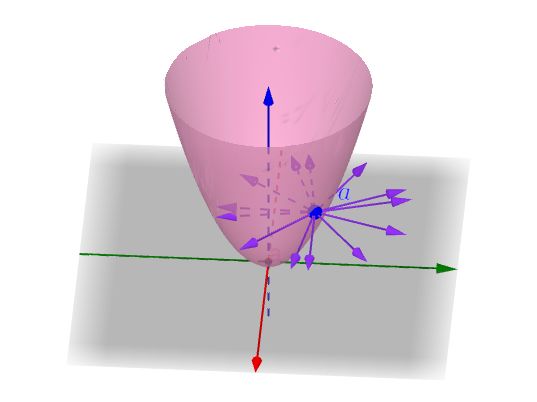
但是!把导数看作是变化率、是切线的斜率,在一元函数的时候是正确的,但是,敲黑板,说但是了哈。在二元函数中,比如这样一个曲面上的一点a,在曲面上可以做无数条过a点的曲线(图上随便画了三根):


把导数看作是变化率、是切线的斜率,在多元函数中是片面的,甚至是不正确的。我们必须要重新审视“导数是什么”这个问题。顺便说一下,把导数继续看作变化率,切线的斜率,可以得到偏导数、方向导数、全导数,可以参看我之前写过的一个回答:什么是全导数? - 知乎
导数是用来找到“线性近似”的数学工具。讲这个之前,我们要先理解微积分的基本思想。这个思想在我的很多回答中都提到了,这里简单的阐述下。
2 导数是用来找到“线性近似”的数学工具
2.1 微积分的基本思想
微积分的基本思想是“以直代曲”:

“以直代曲”的意思就是,切线可以在切点附近很好的近似曲线:

如果在曲线上多选几个点,都作出附近的切线,我们可以透过切线看到曲线的轮廓:

切线可以在切点附近很好的近似曲线。如果仔细看泰勒公式、洛必达法则等,还会通过代数发现这一事实。
2.2 导数是用来找到“线性近似”的数学工具
因为“以直代曲”是微积分的基础,所以我们首要任务就是要找到这个“直”,也就是切线,也就是所谓的“线性近似”。导数就是为了完成这个任务需要使用的数学工具。我们来看看,在一元函数中:

因此,在一元函数中,我们把导数看作斜率,可以找到我们想要的“线性近似”(切线),但是在二元中,我们需要新的技术手段。
3 导数是线性变换
3.1 二元函数的“线性近似”
导数最主要的目的是找到“线性近似”,在一元函数的时候是要找到切线,在二元函数的时候是要找到一个切平面(可以参考我之前的回答:求解全微分的意义?最好感性一点的认识 - 知乎)
3.2 线性变换
对线性代数不熟悉的话,可以先看下我之前的回答 如何通俗地讲解「仿射变换」这个概念? - 知乎。下面就会用到大量的线性代数基础知识,我不再进行解释了。还是从一元的时候开始推:

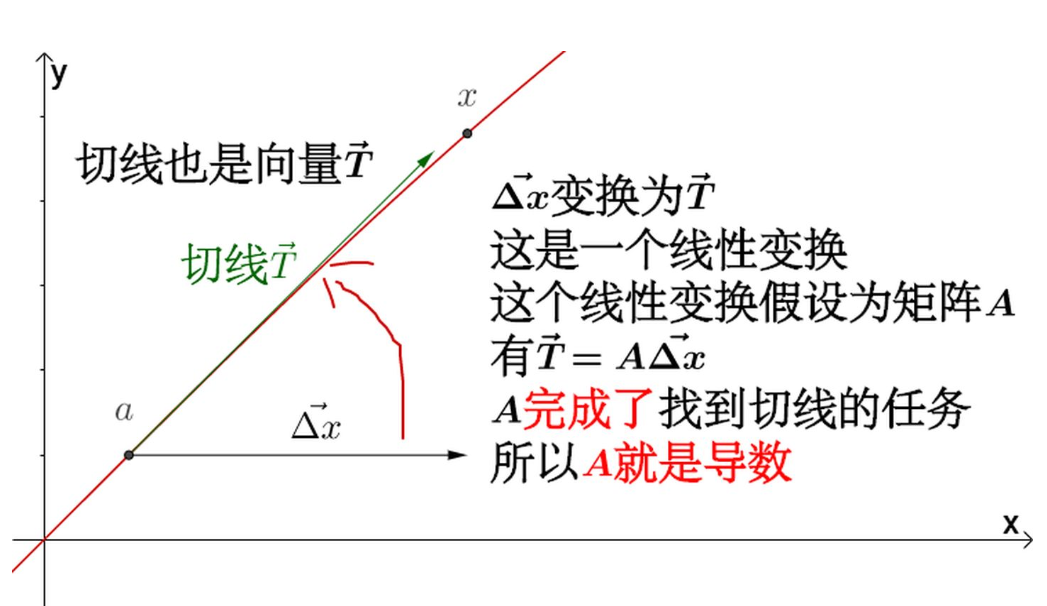
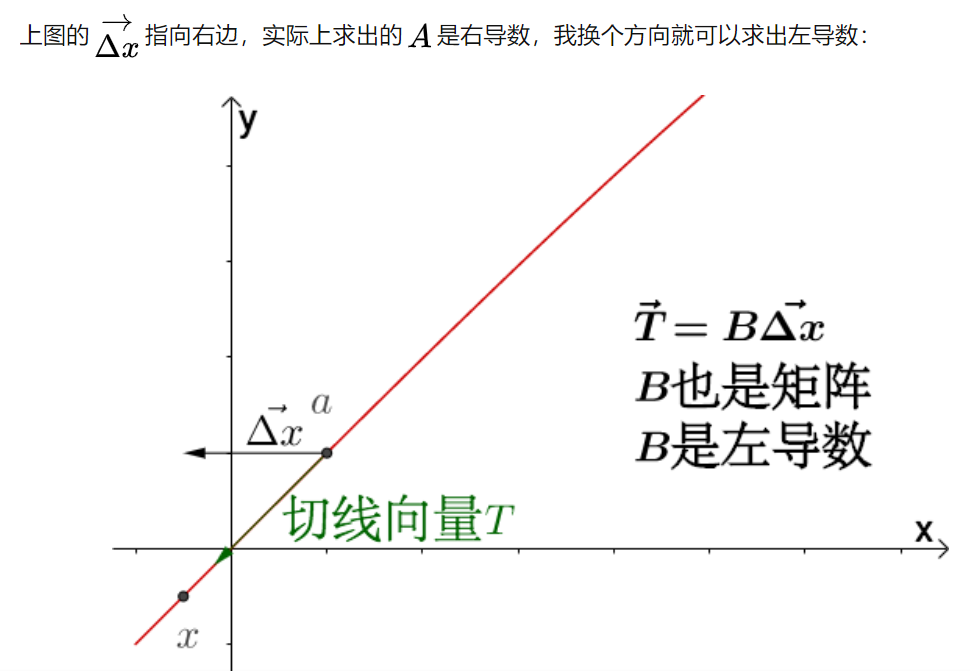


3.3 通过导数A来找到切平面



至此,导数完成了找到“线性近似”的任务。这里也很自然的回答了“多元微积分中,可微函数的切线为什么会共面(此平面即切平面)?”
























 2947
2947

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








