Fourier分析入门——第2章——正弦曲线、相量和矩阵

ComputerInBook

已于 2023-05-27 16:38:22 修改

阅读量726

点赞数

分类专栏：数学与应用数学文章标签：矩阵线性代数相量正弦波傅里叶

于 2023-05-15 23:52:18 首次发布

本文链接：https://blog.csdn.net/ComputerInBook/article/details/130694859

版权

数学与应用数学专栏收录该内容

85 篇文章 11 订阅

订阅专栏

第 2 章正弦曲线，向量，矩阵

2.1 正弦波的向量表示(Phasor representation of sinusoidal waveforms)

2.2 矩阵代数(Matrix algebra)

2.2.1 旋转矩阵(Rotation matrices)

2.2.2 基向量(Basis vectors)

2.2.3 基向量和正交分解的变化

第 2 章正弦曲线，向量，矩阵

2.1 正弦波的向量表示(Phasor representation of sinusoidal waveforms)

正弦波具有两个属性，幅度(或称“大小”)(magnitude)和相位(phase)(译注：“相”指“可视，出现，重现”，而不是“方向”，“相位”即决定周期性的波某个状态位置再现的物理量)，因此正弦波是用相量表示的天然候选者(译注：相量是向量的特例)。为什么选择用相量表示正弦波？

原因之一在于它简化了正弦波形的描述，因为完整的空间或时间波形简化为(复平面中)仅由相量箭头尖端表示的单个点(译注：相量表示正弦波在计算时更为简单)。此外，随着相位角 Φ 与时间成比例增加，箭头尖端在复平面中的轨迹(trajectory)再现了随时间或空间发展的波形变化。

-----------------------------图2.1 正弦波的相量表示--------------------------

原因之二在于它可以帮助我们形象地理解任意正弦波如何分解为纯正弦波形和纯余弦波形的总和。如练习 1.4 所示，使用三角函数执行分解是一项乏味的工作(译注：计算复杂)。然而，如果正弦曲线由相量表示，那么在第1章中使用的向量正交分解法可用于将正弦曲线分解为其正交正弦和正交余弦分量。这种方法如图 2.2 所示。

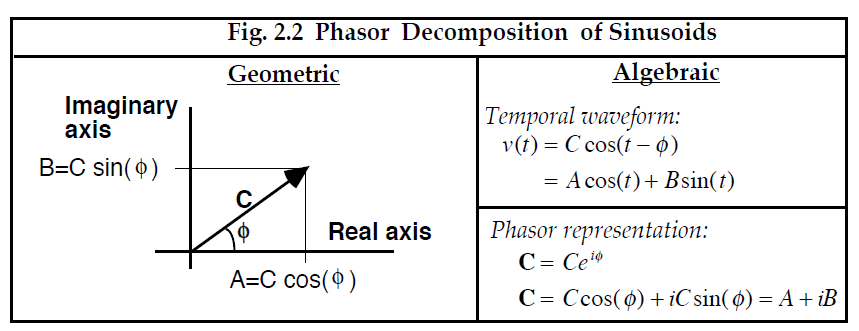
(译注：Temporal waveform(时间波形)。)

-----------------------------图2.2 正弦波的相量分解--------------------------

相量C在代数上可以按两种方式表示。按极坐标形式表示时，相量C是调制信号(modulation)的幅度(amplitude)C与表示波形相位的复数指数 $e^{i\phi}$ 的乘积。令相位随时间线性变化，就会重新创建波形。按笛卡尔坐标形式表示时，C是“实(real)”量(余弦分量的幅度)与“虚(imaginary)”量(正弦分量的幅度)之和。这些表示法的优点在于可以使用基本的代数加法和乘法对正弦曲线进行相加和缩放，而无需求助于繁琐的三角函数。例如，时间波形 v(t)和ω(t)分别用相量P和Q表示，则其和v(t) + ω(t)对应于图1.8中的向量 P + Q 。类似地，如果波形v(t)通过一个按以复数Q所描述的方式进行幅度伸缩和相位变换的滤波器，则滤波器的输出将会对应图1.9所示的相量 S = PQ。

2.2 矩阵代数(Matrix algebra)

如第 1 章所示，两个向量的内积反映了两个向量指向同一方向的程度。因此，内积对于确定一个向量在另一个向量方向上的分量很有用。在练习 1.1 中发现计算内积的紧凑公式是

$d = \sum_{i=1}^{N}(a_i b_i) = sum(a.*b) = dot(a,b)$ -------------------------------------[2.1]

[注：Courier 字体的文本表示 MATLAB 命令]。

矩阵代数中常用的内积的另一种表示法产生相同的答案(但具有符号差异，a.*b 对 a*b’)：

$d =\begin{bmatrix} a_1& a_2& a_3 \end{bmatrix}.\begin{pmatrix} b_1\\ b_2 \\ b_3 \end{pmatrix} = a*b{}'$ (如果,a,b 是行向量)

------------------------------------= a’*b (如果,a,b 是列向量) ----------------------------------------[2.2]

最初，等式[2.1]、[2.2] 是为具有实值元素的向量开发的。要推广内积的概念以处理复数值元素的情况，必须首先将其中一个向量转换为其复共轭(conjugate)。这是获得正确答案所必需的，正如我们在第 1 章讨论相量的长度或复数的大小时所发现的那样。线性代数的标准教科书(例如 Ben Nobel 的 Applied Linear Algebra (线性代数的应用)) 和 MATLAB计算语言采用将计算的两个向量中的第一个共轭(即改变列向量虚部的符号)的约定。因此，对于复值列向量，等式2.2 重写为

$d = \begin{bmatrix} a_{1}^* & a_{2}^* & a_{3}^* \end{bmatrix}.\begin{bmatrix} b_1\\ b_2 \\ b_3 \end{bmatrix}= sum(conj(a).*b) =dot(a,b) =a'*b----[2.3]$

因为等式[2.2]对于实数向量只是[2.3]对于复值向量的特例，所以许多教科书使用更通用、更复杂的符号来发展理论。在 Matlab 中，相同的符号适用于这两种情况。但是，顺序对于复值向量很重要，因为 dot(a,b) = (dot(b, a))* 。为了使代数符号尽可能简单，我们将继续假设向量和矩阵的元素是实值的，直到后面的章节。

矩阵符号的一个优点是它很容易扩展以允许向量与矩阵相乘以计算一系列内积。例如，矩阵方程

$\begin{bmatrix} p_1\\ p_2 \\ p_3 \end{bmatrix}=\begin{bmatrix} a_1 & a_2 &a_3 \\ b_1&b_2 & b_3\\ c_1& c_2 &c_3 \end{bmatrix}.\begin{bmatrix} d_1\\d_2 \\ d_3 \end{bmatrix}$ -------------------------------------------------------------[2.4]

解释为指的是：“执行(行)向量 a 与(列)向量 d 的内积，并将结果存储为向量 p 的第一个分量。接下来，执行(行)向量 b 与(列)向量 d 的内积，并将结果存储为向量 p 的第二个分量。最后，将(行)向量 c 与(列)向量 d 进行内积，并将结果存储为向量 p 的第三个分量。” 换句话说，可以通过将矩阵分解为行向量并依次对每一行执行给定向量的内积来计算矩阵和向量的乘积。简而言之，矩阵乘法只不过是将一个向量转换为另一个向量的重复内积。

等式 [2.4] 的形式提出了一种非常通用的方案，用于将“输入”向量 d 转换为“输出”向量 p 。也就是说，我们可以说，如果 p = [M].d，则矩阵 M 已将向量 d 转换为向量 p 。通常 M 的元素被认为是“加权因子(weighting factors)”，应用于向量 d 以产生 p。例如，输出向量 p 的第一个分量等于输入向量分量的加权和，即，

$p_1 = a_1 d_1 + a_2 d_2 + a_2 d_2$ ----------------------------------------------------------------[2.5]

因为输入向量的加权分量(按线性的方式)加在一起以产生输出向量，所以矩阵乘法称为线性转换(或称线性变换)(linear transform),这就解释了为什么矩阵代数(matrix algebra)也称为线性代数(linear algebra)。

矩阵代数广泛用于描述线性物理系统，可以将其视为将输入信号转换为输出信号。例如，来自麦克风(microphone)的电信号被数字化并作为一系列向量数据记录在光盘上(compact disk)，每个向量表示一个瞬间的信号强度。这些向量的后续放大和滤波以改变音高(pitch)或响度(loudness)是通过将这些输入向量中的每一个乘以适当的矩阵来产生一系列输出向量，然后驱动扬声器产生声音来完成的。来自视觉科学(vision science)的例子包括眼睛光学系统(optical system)对光图像的处理、视觉通路(visual pathways)内神经图像(neural images)的视网膜(retinal)和皮质(cortical)处理的线性模型，以及眼睛旋转(eye rotations)的运动学(kinematic)控制。

2.2.1 旋转矩阵(Rotation matrices)

通常，矩阵乘法的结果是向量的长度和方向都发生变化。但是，对于某些矩阵，向量的长度保持不变，只有方向发生变化。这种在不改变向量长度的情况下旋转向量的特殊矩阵称为旋转矩阵(译注：方向改变时向矩阵的大小会改变)。图 2.3 说明了转置的几何形状。

----------------------------------------------图2.3 旋转矩阵--------------------------------------------------

假如原向量的坐标是(x , y ), 则按角度δ 旋转后的向量坐标(u , v )为

u = Rcos(α + δ )

v = Rsin(α + δ )。----------------------------------------------------------[2.6]

应用三有恒等

cos(α + δ ) = cos(α) cos(δ )- sin(α) sin(δ )

sin(α + δ ) = cos(α) sin(δ )+ sin(α) cos(δ ) 。---------------------------------[2.7]

以上是练习1.2的主题，得到

u = R cos(α) cos(δ )- R sin(α) sin(δ )

v = R cos(α) sin(δ )+ R sin(α) cos(δ ) 。-------------------------------------[2.8]

但因为 R* cos(α) = 𝘹 ，R* sin(α) = 𝘺，我们有

u = 𝘹 cos(δ )- 𝘺 sin(δ )

v = 𝘹 sin(δ )+ 𝘺 cos(δ ) 。---------------------------------------------------[2.9]

我们将以上等式用矩阵的旋转表示为

$\begin{bmatrix} u \\ v \end{bmatrix}=\begin{bmatrix} cos(\delta )& -sin(\delta )\\ sin(\delta)& cos(\delta) \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$ 。--------------------------------------------[2.10]

基于这个二维旋转矩阵的例子，我们可以得出某些结论，无论矩阵的维数如何，这些结论都是正确的。请注意，如果 [2.10] 中旋转矩阵的每一行都被视为一个向量，则每一行与其他每一行的内积为零。这同样适用于矩阵的列。换句话说，旋转矩阵的行和列是相互正交的。这样的矩阵称为正交矩阵(orthogonal matrix)。此外，请注意，旋转矩阵的每个行向量或列向量的长度是单位(unity)。这样的矩阵称为正规矩阵(normal matrix)。旋转矩阵具有这两种性质，因此称为正交正规矩阵(ortho-normal-matrix)。稍加思考就会使学生相信正交属性负责输入向量的旋转，而正规属性负责保持比例。

鉴于这些结论，应该预期类似的方程会将输出向量 p 旋转回原始输入向量 d。换句话说，旋转变换是可逆的。因此，假如

p = M.d -----------------------------------------------------------------[2.11]

则等式两别分别乘以M的逆矩阵 $M^{-1}$ 产生

$M^{-1}p = M^{-1}M.d$ 。-------------------------------------------------------[2.12]

由于任何矩阵乘以它的逆等于单位矩阵 I(正对角线元素上为1，其他地方为0)，结果是

$M^{-1}p = I.d$ 。------------------------------------------------------------[2.13]

虽然，求逆矩阵一般来说是一件困难的事情，但对于旋转矩阵来说求逆矩阵却非常容易。正交矩阵的逆矩阵只是矩阵的转置(transpose)，它通过交换行和列来确定(即关于它的正对角线翻转矩阵)。因此 [2.10] 的互补等式是

$\begin{bmatrix} u \\ v \end{bmatrix}=\begin{bmatrix} cos(\delta )& sin(\delta )\\ -sin(\delta)& cos(\delta) \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$ 。-------------------------------------------[2.15]

2.2.2 基向量(Basis vectors)

为了准备学习Fourier分析，复习后面提到的线性代数的概念和术语是很有必要的。如果 u 和 v 是指向不同方向的非零向量，则它们是线性无关的(linearly independent)。在这一点上必须避免使用短语“不同方向(different direction)”的潜在陷阱。在日常英语用法中，北方和南方被认为是相反的方向。然而，方向一词的当前数学用法依据内积法则，最好将正交方向 “北(North)” 和 “东(East)” 视为相反方向，而将“北(North)” 和 “南(South)” 方向视为符号相反的相同方向。考虑到这一点，线性独立思想的更精确表达是要求两个向量之间夹角的余弦值不为±1，这等同于说| u • v |≠| u |.| v |(译注：即两个向量不能在同一条直线上，必需呈一定的倾斜角，否则，一个相同总可能用另一个向量表示，则不具有线性独立性)。给定两个线性无关的向量 u 和 v，在 u 和 v 的平面上的任何向量 c 都可以通过线性组合 c = A u + B v 找到。为此，线性独立(但不一定正交)(译注：正交则意味着两个向量之间的方向“完全相反，没有任何同向性”)向量 u 和 v 被称为构成它们所在平面的二维空间的基础(basis)(译注：基础简称“基”，即，有了这个基础，其它向量都可以由这两个基础按一定的线性组合表示出来)。由于任何一对线性无关的向量都将跨越它们自己的空间，因此有无限多的向量对构成空间的基础。如果一对特定的基向量恰好是正交的(即 u•v = 0)，则它们为空间提供了正交基。例如，笛卡尔坐标系的传统 𝘟–𝘠 轴形成二维空间的正交基。正交基向量通常比非正交基向量更方便用作坐标参考系，因为每个向量在另一个方向上的分量为零。

上述表述可以推广到更高维空间，如下所示。N 维空间将由任意一组 N 个线性无关向量构成，这意味着该集合中的每个向量必须指向不同的方向。如果所有 N 个向量相互正交，则它们构成空间的正交基。如下一章所示，Fourier分析可以被认为是从普通笛卡尔坐标到基于三角正弦函数和余弦函数的正交向量集的基础变化。

2.2.3 基向量和正交分解的变化

给定一个由其在同一个参考系(frame)中的坐标指定的向量，我们可能希望在另一个参考系中指定相同的向量。这与更改给定向量所在空间的基向量是同一个问题。如果新的基向量相互正交，则该过程也可以描述为将给定向量分解为正交分量。 (例如，Fourier分析是将测量向量正交分解为表示Fourier系数的参考系。在几何上，这种分解对应于通过旋转和重新缩放改变基向量。) 通过在几何上思考这个变更基向量问题，并回顾一个向量到另一个向量的投影是通过内积计算的，这就引出了基向量变更的代数描述。例如，矢量 V 在 𝘹 方向上的分量是通过形成 V 与单位基向量 𝘹 =[1,0] 的内积来计算的。类似地，矢量 V 在 𝘺 方向上的分量通过形成 V 与单位基向量 𝘺 =[0,1] 的内积来计算。这些操作对应于原始向量 V 与单位矩阵的乘法，如图 2.4 所示。

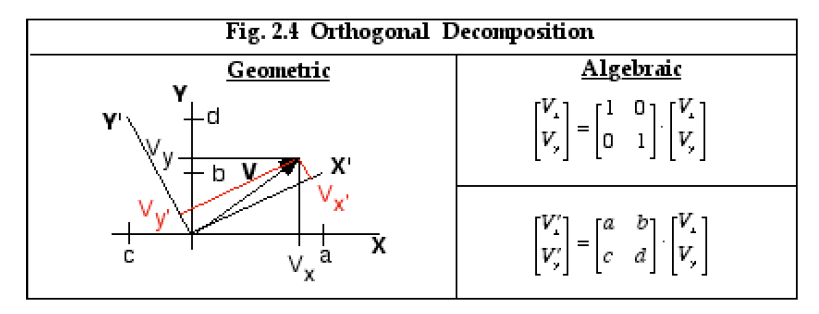
-----------------------------图2.4 正交分量----------------------------------

通常，如果正交基向量 𝘹', 𝘺' 的 (x ,y) 坐标是 𝘹' = [a,b] 和 𝘺' = [c,d]，那么 V 在 (x', y') 坐标系中的坐标是按如下方式将 $V = (V_x, V_y)$ 的坐标投影到 (x', y')轴上来计算：

$V_(x') = V$ 在 x'方向上的分量 = $[a,b]\cdot [V_x, V_y]'$ [V 在x'上的投影]

$V_(y') = V$ 在 y'方向上的分量 = $[c,d]\cdot [V_x, V_y]'$ [V 在y'上的投影]

这一对方程可以用矩阵简记为

$\begin{bmatrix} V_{x'}\\ V_{y'} \end{bmatrix}=\begin{bmatrix} a &b \\ c& d \end{bmatrix}.\begin{bmatrix} V_{x}\\ V_{y} \end{bmatrix}$ ---------------------------------------------------[2.16]