MIT18.06学习笔记 - Lecture 3: Multiplication and Inverse Matrices

最新推荐文章于 2022-09-03 08:00:00 发布

CrazyTensor

最新推荐文章于 2022-09-03 08:00:00 发布

阅读量478

点赞数 1

分类专栏： math 文章标签： linear algebra

本文链接：https://blog.csdn.net/CrazyTensor/article/details/80934528

版权

这个系列文章是我重温Gilbert老爷子的线性代数在线课程的学习笔记。
Course Name：MIT 18.06 Linear Algebra
Text Book: Introduction to Linear Algebra
章节内容: 2.4-2.5

课程提纲
1. Matrix Multiplication (5 ways)
2. The laws for Matrix Operations
3. Inverse Matrices
4. Gauss-Jordan Elimination

课程重点

Row echelon form resulting from Gaussian elimination: an upper triangular matrix $U$ .
Reduced row echelon form computed by Gauss–Jordan elimination: all of the leading coefficients (the leftmost nonzero entry in each row) are 1, and every column containing a leading coefficient has zeros elsewhere, it is unique and independent of the sequence of row operations used. For example, the third and fourth matrices are the ones in row echelon form, and the final matrix is the unique reduced row echelon form:

Matrix Multiplication (5 ways)

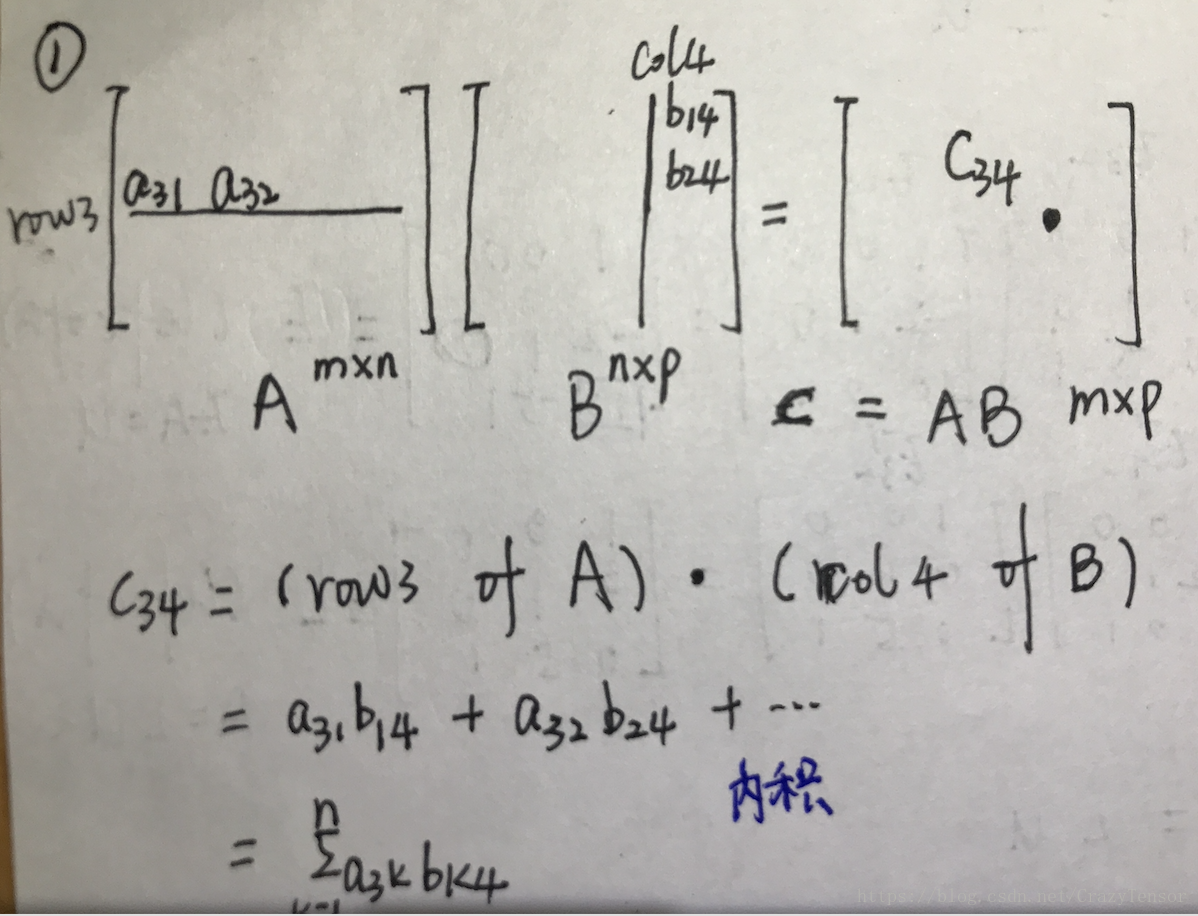
1. Entry view, the entry in row $i$ and column $j$ of $AB$ is (row $i$ of $A$ ) $\cdot$ (column $j$ of $B$ ):

2. Column view, columns of $C$ are combinations of columns of A:

3. Row view, rows of $C$ are combinations of rows of B:

4. Outer product view, $AB$ adds up columns times rows, important special case of block view:

Compare it with the usual rows times columns. Row 1 of $A$ times column 1 of $B$