大物大杂烩

一：质点运动学。

1：圆周运动（求切向加速度，法相加速度，总加速度）

阿尔法为角加速度。
例题：

注：
切向加速度=角加速度*R
这里面：贝塔=欧米伽

这里面的阿尔法就是角加速度（贝塔）。

2：相对运动。

绝对速度：大自然的例风…
相对速度：人或人骑自行车等的运动。
牵连速度：人感觉到风的速度。

二：质点动力学。

1：保守力。

关于木块拉动的题：
动量，冲量，动量定理的题：
弹簧的题：
能量守恒，动量守恒的题：

三：刚体力学。

1：角加速度，角速度

n为转速。
例题：
2：转动惯量：J

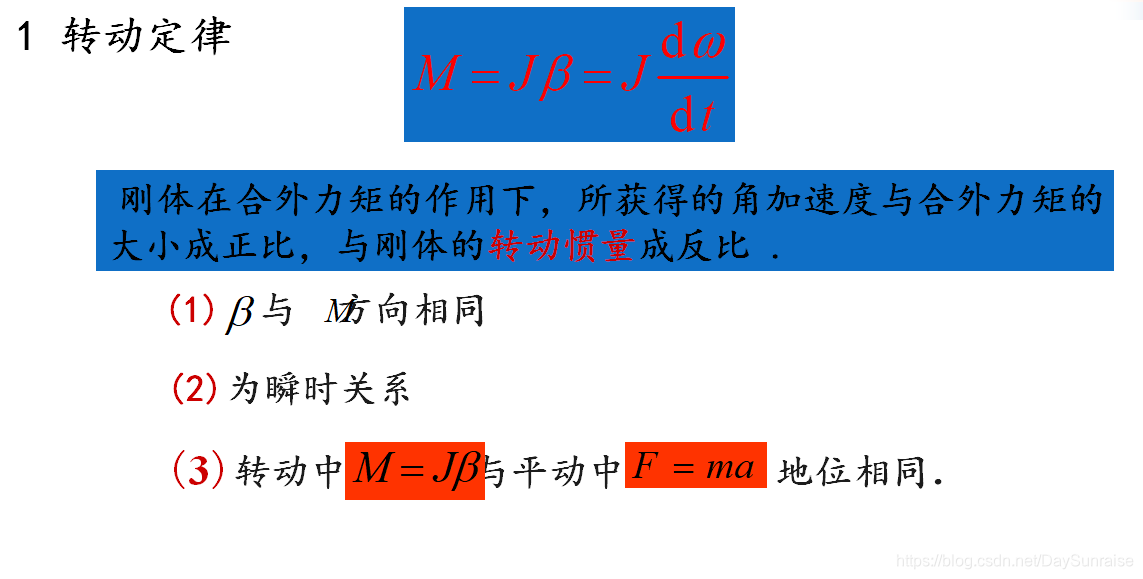
注：M为力矩。M总=J乘以角加速度。M=FR ; M总=F1R1+F2R2…
例题：
注：角加速度等于切向加速度除以半径。即切向加速度= 半径®乘以角加速度。
再来一道题：
注:M=FR。M为力矩。M总=J乘以角加速度。M=FR ; M总=F1R1+F2R2…

四：气体动理论。（m/M=物质的量（n））

理论知识：

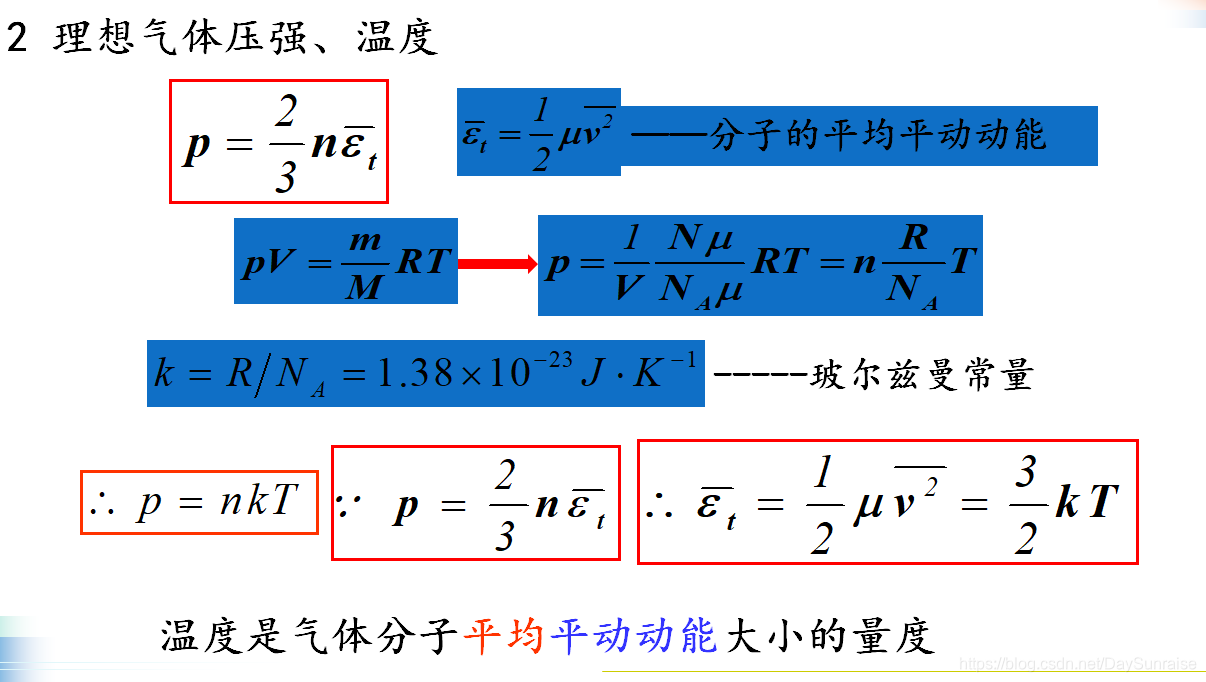
注：其中的 n=N/V（即单位体积分子得个数）

常见元子的自由度：
（1）单原子分子：如氦He、氖Ne、氩Ar等分子只有一个原子，可看成自由质点，所以有3个平动自由度 i = t =3　
　（ 2）刚性双原子分子如氢 、氧 、氮 、一氧化碳CO等分子，两个原子间联线距离保持不变。就像两个质点之间由一根质量不计的刚性细杆相连着（如同哑铃），确定其质心O’的空间位置，需3个独立坐标（x，y，z）；确定质点联线的空间方位，需两个独立坐标（如α，β），而两质点绕联线的的转动没有意义。所以刚性双原子分子既有3个平动自由度，又有2个转动自由度，总共有5个自由度 i = t + r =3 + 2 = 5。　
　（3）刚性三原子或多原子分子：如 H2O 、氨 等，只要各原子不是直线排列的，就可以看成自由刚体，共有6个自由度，i = t + r = 3 + 3 = 6。
　(4)　对于非刚性分子，由于在原子之间相互作用力的支配下，分子内部还有原子的振动，因此还应考虑振动自由度（以S 表示）。如非刚性双原子分子，好像两原子之间有一质量不计的细弹簧相连接，则振动自由度 S = 1。
　　一般在常温下，气体分子都近似看成是刚性分子，振动自由度可以不考虑。


u就是质量。

例题：

1：
:2：
注：此题应为pv=m/M*RT=nRT

总结：公式

压强：

内能：
速率：

五：热力学基础。

公式：

：

例题：
1：

v=n(物质的量)
物态方程式：
pv=nRT
2：

理想气体等温膨胀时：
pV=nRT为定值,所以p=nRT/V,W=积分pdV=nRTln(V’/V)
注：上面的公式应为：
WAB=PAVA*LN(VB/VA)
3：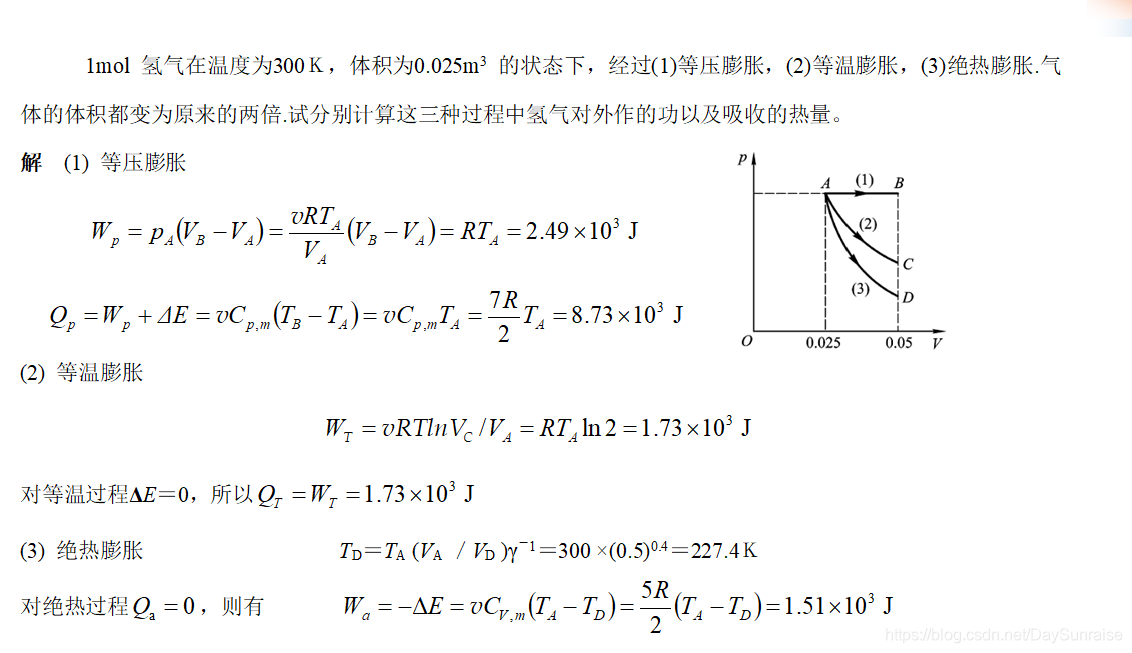
释：

公式应为：
TD=TA(VA/VD)的嘎码减1次方。

六：静电场。

例题：
1：

释：E=q/（4π依科西弄 r方）
2：
释：
扇形弧长L=R角度
3：