高等数学笔记-乐经良老师
第九章 重积分
第一节 二重积分的概念和性质
一、典型例子
01 平面薄板的质量
平面薄板位于 x y xy xy 平面区域 D D D,其面密度为 μ ( x , y ) μ(x,y) μ(x,y) 如何求其质量?
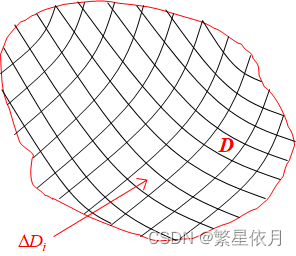
类似一元的处理方法,采用:
(1) 分割
将 D D D 任意划分成 n n n 个小区域 Δ D 1 , Δ D 2 , ⋯ , Δ D n , Δ D i \Delta D_{1}, \Delta D_{2}, \cdots, \Delta D_{n}, \Delta D_{i} ΔD1,ΔD2,⋯,ΔDn,ΔDi 的面积记为 Δ σ i , ( i = 1 , 2 , ⋯ , n ) \Delta \sigma_{i},(i=1,2, \cdots, n) Δσi,(i=1,2,⋯,n)
(2) 作和
在小区域分得很小时,近似认为质量均匀,任取
(
ξ
i
,
η
i
)
∈
Δ
D
i
\left(\xi_{i}, \eta_{i}\right) \in \Delta D_{i}
(ξi,ηi)∈ΔDi,薄板的质量近似地表达为
m
=
∑
i
=
1
n
Δ
m
i
≈
∑
i
=
1
n
μ
(
ξ
i
,
η
i
)
Δ
σ
i
m=\sum_{i=1}^{n} \Delta m_{i} \approx \sum_{i=1}^{n} \mu\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}
m=i=1∑nΔmi≈i=1∑nμ(ξi,ηi)Δσi
(3) 取极限
记
λ
=
max
1
≤
1
≤
n
{
d
i
}
\lambda=\max \limits_{1 \leq 1 \leq n}\left\{d_{i}\right\}
λ=1≤1≤nmax{di},(
d
i
d_{i}
di 是小区域
Δ
D
i
\Delta D_{i}
ΔDi 的直径 ) 那么若
m
=
lim
λ
→
0
∑
i
=
1
n
μ
(
ξ
i
,
η
i
)
Δ
σ
i
m=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} \mu\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}
m=λ→0limi=1∑nμ(ξi,ηi)Δσi
存在,就给出了薄板的质量。
02 曲顶柱体的体积
柱体的侧面是母线垂直 x y x y xy 平面的柱面,顶面为曲面 S : z = f ( x , y ) S: z=f(x, y) S:z=f(x,y),
底面是 x y x y xy 平面上区域 D D D,如何求此曲顶柱体的体积?
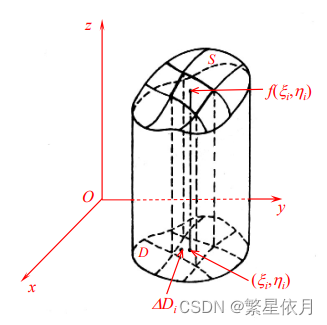
(1) 分割
用曲线将 D D D 分成小区域 Δ D 1 , Δ D 2 , ⋯ , Δ D n \Delta D_{1}, \Delta D_{2}, \cdots, \Delta D_{n} ΔD1,ΔD2,⋯,ΔDn,而 Δ D i \Delta D_{i} ΔDi 的面积记为 Δ σ i \Delta \sigma_{i} Δσi
(2) 求和
区域分得很小时,用柱体来近似小曲顶柱体的体积,任取
(
ξ
i
,
η
i
)
∈
Δ
D
i
\left(\xi_{i}, \eta_{i}\right) \in \Delta D_{i}
(ξi,ηi)∈ΔDi,则总体积近似为
∑
i
=
1
n
f
(
ξ
i
,
η
i
)
Δ
σ
i
\sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}
i=1∑nf(ξi,ηi)Δσi
(3) 取极限
记
λ
=
max
1
≤
1
≤
n
{
d
i
}
\lambda=\max \limits_{1 \leq 1 \leq n}\left\{d_{i}\right\}
λ=1≤1≤nmax{di},(
d
i
d_{i}
di 是小区域
Δ
D
i
\Delta D_{i}
ΔDi 的直径 ) 则体积
V
V
V 由如下极限给出
V
=
lim
λ
→
0
∑
i
=
1
n
f
(
ξ
i
,
η
i
)
Δ
σ
i
V=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}
V=λ→0limi=1∑nf(ξi,ηi)Δσi
从以上例子抽象出来就得到二重积分的概念,这类问题要计算在一个平面区域上分布率不均匀的量的总量。
二、二重积分定义
01 二重积分的定义
设 D D D 是 x y x y xy 平面的有界闭区域,函数 f ( x , y ) f(x, y) f(x,y) 在 D D D 定义, I I I 为实数,
若将 D D D 任意划分成个小区域 Δ D 1 , Δ D 2 , ⋯ , Δ D n \Delta D_{1}, \Delta D_{2}, \cdots, \Delta D_{n} ΔD1,ΔD2,⋯,ΔDn,
任取
(
ξ
i
,
η
i
)
∈
Δ
D
i
,
(
i
=
1
,
2
,
⋯
,
n
)
\left(\xi_{i}, \eta_{i}\right) \in \Delta D_{i},(i=1,2, \cdots, n)
(ξi,ηi)∈ΔDi,(i=1,2,⋯,n),作和
∑
i
=
1
n
f
(
ξ
i
,
η
i
)
Δ
σ
i
(
Δ
σ
i
表示
Δ
D
i
的面积
)
\sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i} \quad\left(\Delta \sigma_{i}\right. 表示 \Delta D_{i} 的面积 )
i=1∑nf(ξi,ηi)Δσi(Δσi表示ΔDi的面积)
总有
lim
λ
→
0
∑
i
=
1
n
f
(
ξ
i
,
η
i
)
Δ
σ
i
=
I
\lim \limits_{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}=I
λ→0limi=1∑nf(ξi,ηi)Δσi=I
( 其中
λ
=
max
1
≤
i
≤
n
{
d
i
}
\lambda=\max \limits_{1 \leq i \leq n}\left\{d_{i}\right\}
λ=1≤i≤nmax{di},
d
i
d_{i}
di 是小区域
Δ
D
i
\Delta D_{i}
ΔDi 的直径 )
则称函数 f ( x , y ) f(x, y) f(x,y) 在 D D D 上可积, I I I 称为 f ( x , y ) f(x, y) f(x,y) 在 D D D 的二重积分,记为 ∬ D f ( x , y ) d σ \iint \limits_{D} f(x, y) d \sigma D∬f(x,y)dσ .
其中, ∬ − \iint- ∬− 积分号, D − D- D− 积分区域, f ( x , y ) − f(x, y)- f(x,y)−被积函数, d σ − d \sigma- dσ−面积元素。
02 二重积分的几何意义
以区域 D D D 为底,以曲面 S : z = f ( x , y ) S: z=f(x, y) S:z=f(x,y) 为顶的曲顶柱体的体积。
03 可积的充分条件
若函数 f ( x , y ) f(x, y) f(x,y) 在有界区域 D D D 上分片连续有界,则 f ( x , y ) f(x, y) f(x,y) 在 D D D 可积。
三、二重积分的性质
设以下性质中出现的积分均存在
-
性质1 (线性) :若 α , β \alpha, \beta α,β 是常数,
∬ D ( α f ( x , y ) + β g ( x , y ) ) d σ = α ∬ D f ( x , y ) d σ + β ∬ D g ( x , y ) d σ \iint \limits_{D}(\alpha f(x, y)+\beta g(x, y)) d \sigma=\alpha \iint \limits_{D} f(x, y) d \sigma+\beta \iint \limits_{D} g(x, y) d \sigma D∬(αf(x,y)+βg(x,y))dσ=αD∬f(x,y)dσ+βD∬g(x,y)dσ -
性质2 (可加性) :若积分区域 D D D 分成 D 1 , D 2 D_{1}, D_{2} D1,D2 两个子区域,
∬ D f ( x , y ) d σ = ∬ D 1 f ( x , y ) d σ + ∬ D 2 f ( x , y ) d σ \iint \limits_{D} f(x, y) d \sigma=\iint \limits_{D_{1}} f(x, y) d \sigma+\iint \limits_{D_{2}} f(x, y) d \sigma D∬f(x,y)dσ=D1∬f(x,y)dσ+D2∬f(x,y)dσ -
性质3:
∬ D 1 d σ = A D ( D 的面积 ) \iint \limits_{D} 1 d \sigma=A_{D} \quad(D\ 的面积) D∬1dσ=AD(D 的面积) -
性质4 (单调性) :若 f ( x , y ) ≤ g ( x , y ) f(x, y) \leq g(x, y) f(x,y)≤g(x,y),则
∬ D f ( x , y ) d σ ≤ ∬ D g ( x , y ) d σ \iint \limits_{D} f(x, y) d \sigma \leq \iint \limits_{D} g(x, y) d \sigma D∬f(x,y)dσ≤D∬g(x,y)dσ
性质4的推论:
( 1 ) 若 f ( x , y ) ≥ 0 , 则 ∬ D f ( x , y ) d σ ≥ 0 ( 2 ) ∣ ∬ D f ( x , y ) d σ ∣ ≤ ∬ D ∣ f ( x , y ) ∣ d σ ( 三角不等式的推广 ) ( 3 ) 若 m ≤ f ( x , y ) ≤ M , 则 m A D ≤ ∬ D f ( x , y ) d σ ≤ M A D \begin{aligned} & (1)\ \ 若 f(x, y) \geq 0, 则 \iint \limits_{D} f(x, y) d \sigma \geq 0\\ & (2)\ \ \left|\iint \limits_{D} f(x, y) d \sigma\right| \leq \iint \limits_{D}|f(x, y)| d \sigma \ \ \ (三角不等式的推广) \\ & (3)\ \ 若 m \leq f(x, y) \leq M, 则\ m A_{D} \leq \iint \limits_{D} f(x, y) d \sigma \leq M A_{D} \end{aligned} (1) 若f(x,y)≥0,则D∬f(x,y)dσ≥0(2) D∬f(x,y)dσ ≤D∬∣f(x,y)∣dσ (三角不等式的推广)(3) 若m≤f(x,y)≤M,则 mAD≤D∬f(x,y)dσ≤MAD -
性质5 (中值定理) :若 D D D 是有界闭区域, f ( x , y ) ∈ C ( D ) f(x, y) \in C(D) f(x,y)∈C(D),则存在 ( ξ , η ) ∈ D (\xi, \eta) \in D (ξ,η)∈D,
∬ D f ( x , y ) d σ = f ( ξ , η ) A D \iint \limits_{D} f(x, y) d \sigma=f(\xi, \eta) A_{D} D∬f(x,y)dσ=f(ξ,η)AD
对应一元函数定积分中的平均值定理(积分第一中值定理)
第二节 二重积分的计算
一、直角坐标系下的计算
01 x x x 型正则区域
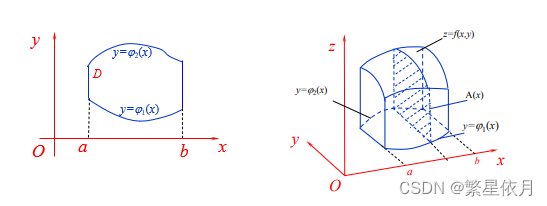
设区域 D = { ( x , y ) ∣ a ≤ x ≤ b , φ 1 ( x ) ≤ y ≤ φ 2 ( x ) } D=\left\{(x, y) \mid a \leq x \leq b, \varphi_{1}(x) \leq y \leq \varphi_{2}(x)\right\} D={(x,y)∣a≤x≤b,φ1(x)≤y≤φ2(x)}
二重积分 ∬ D f ( x , y ) d x d y \iint \limits_{D} f(x, y) d x d y D∬f(x,y)dxdy ( d σ = d x d y ) (d \sigma=d x d y) (dσ=dxdy) 的值
等于以 D D D 为底,以曲面 S S S : z = f ( x , y ) z=f(x, y) z=f(x,y) 为顶的曲顶柱体的体积。
利用定积分来求体积考虑垂直 x x x 轴过 x x x 处的平面截曲顶柱体所得截面积 A ( x ) A(x) A(x)
截面曲边梯形的面积
A
(
x
)
A(x)
A(x)
A
(
x
)
=
∫
φ
1
(
x
)
φ
2
(
x
)
f
(
x
,
y
)
d
y
\mathrm{A}(x)=\int_{\varphi_{1}(x)}^{\varphi_{2}(x)} f(x, y) d y
A(x)=∫φ1(x)φ2(x)f(x,y)dy
可得曲顶柱体的体积
V
=
∫
a
b
A
(
x
)
d
x
=
∫
a
b
(
∫
φ
1
(
x
)
φ
2
(
x
)
f
(
x
,
y
)
d
y
)
d
x
V=\int_{a}^{b} \mathrm{~A}(x) d x=\int_{a}^{b}\left(\int_{\varphi_{1}(x)}^{\varphi_{2}(x)} f(x, y) d y\right) d x
V=∫ab A(x)dx=∫ab(∫φ1(x)φ2(x)f(x,y)dy)dx
导出
∬
D
f
(
x
,
y
)
d
x
d
y
=
∫
a
b
(
∫
φ
1
(
x
)
φ
2
(
x
)
f
(
x
,
y
)
d
y
)
d
x
\iint \limits_{D} f(x, y) d x d y=\int_{a}^{b}\left(\int_{\varphi_{1}(x)}^{\varphi_{2}(x)} f(x, y) d y\right) d x
D∬f(x,y)dxdy=∫ab(∫φ1(x)φ2(x)f(x,y)dy)dx
写成
∬
D
f
(
x
,
y
)
d
x
d
y
=
∫
a
b
d
x
∫
φ
1
(
x
)
φ
2
(
x
)
f
(
x
,
y
)
d
y
\iint \limits_{D} f(x, y) d x d y=\int_{a}^{b} d x \int_{\varphi_{1}(x)}^{\varphi_{2}(x)} f(x, y) d y
D∬f(x,y)dxdy=∫abdx∫φ1(x)φ2(x)f(x,y)dy
02 y y y 型正则区域
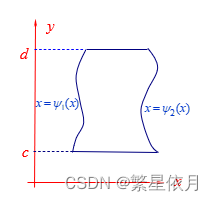
若积分区域
D
=
{
(
x
,
y
)
∣
ψ
1
(
y
)
≤
x
≤
ψ
2
(
y
)
,
c
≤
y
≤
d
}
D=\left\{(x, y) \mid \psi_{1}(y) \leq x \leq \psi_{2}(y), c \leq y \leq d\right\}
D={(x,y)∣ψ1(y)≤x≤ψ2(y),c≤y≤d}
则有
∬
D
f
(
x
,
y
)
d
x
d
y
=
∫
c
d
d
y
∫
ψ
1
(
y
)
ψ
2
(
y
)
f
(
x
,
y
)
d
x
\iint \limits_{D} f(x, y) d x d y=\int_{c}^{d} d y \int_{\psi_{1}(y)}^{\psi_{2}(y)} f(x, y) d x
D∬f(x,y)dxdy=∫cddy∫ψ1(y)ψ2(y)f(x,y)dx
小总结
对于一般区域的二重积分可将其分成若干个正则子区域,
利用积分的可加性,分别在各子区域积分后求和。
当积分区域关于 x x x 轴或 y y y 轴对称时,注意被积函数是否有奇偶性,从而使积分简化。
对称性非常重要!
二、极坐标系下的计算公式
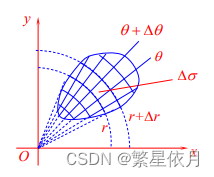
当积分区域的边界曲线或被积函数用极坐标表示较为简单时,二重积分有时可用极坐标来计算
我们来考虑面积元素 Δ σ \Delta \sigma Δσ 在极坐标下的形式
用
r
r
r 为常数所表示的圆周族和
θ
\theta
θ 为常数所表示的射线族分割区域
D
D
D,那么小区域面积
Δ
σ
=
1
2
[
(
r
+
Δ
r
)
2
Δ
θ
−
r
2
Δ
θ
]
=
1
2
[
2
r
Δ
r
+
(
Δ
r
)
2
]
Δ
θ
⟹
d
σ
=
r
d
r
d
θ
\begin{aligned} &\Delta \sigma=\frac{1}{2}\left[(r+\Delta r)^{2} \Delta \theta-r^{2} \Delta \theta\right]=\frac{1}{2}\left[2 r \Delta r+(\Delta r)^{2}\right] \Delta \theta \\ &\Longrightarrow \quad d \sigma=r d r d \theta \end{aligned}
Δσ=21[(r+Δr)2Δθ−r2Δθ]=21[2rΔr+(Δr)2]Δθ⟹dσ=rdrdθ
从直角坐标变换为极坐标时的二重积分的变换公式
∬
D
f
(
x
,
y
)
d
x
d
y
=
∬
D
f
(
r
cos
θ
,
r
sin
θ
)
r
d
r
d
θ
\iint \limits_{D} f(x, y) d x d y=\iint \limits_{D} f(r \cos \theta, r \sin \theta) r d r d \theta
D∬f(x,y)dxdy=D∬f(rcosθ,rsinθ)rdrdθ
若区域
D
=
{
(
r
,
θ
)
∣
r
1
(
θ
)
≤
r
≤
r
2
(
θ
)
,
α
≤
θ
≤
β
}
D =\left\{(r, \theta) \mid r_{1}(\theta) \leq r \leq r_{2}(\theta), \alpha \leq \theta \leq \beta\right\}
D={(r,θ)∣r1(θ)≤r≤r2(θ),α≤θ≤β}
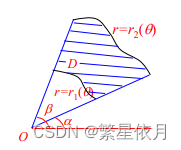
二重积分化为累次积分
∬
D
f
(
r
cos
θ
,
r
sin
θ
)
r
d
r
d
θ
=
∫
α
β
d
θ
∫
r
1
(
θ
)
r
2
(
θ
)
f
(
r
cos
θ
,
r
sin
θ
)
r
d
θ
\iint \limits_{D} f(r \cos \theta, r \sin \theta) r d r d \theta = \int_{\alpha}^{\beta} d \theta \int_{r_{1}(\theta)}^{r_{2}(\theta)} f(r \cos \theta, r \sin \theta) r d \theta
D∬f(rcosθ,rsinθ)rdrdθ=∫αβdθ∫r1(θ)r2(θ)f(rcosθ,rsinθ)rdθ
三、二重积分的变量代换
设变换
{
x
=
x
(
u
,
v
)
y
=
y
(
u
,
v
)
\left\{\begin{array}{l}x=x(u, v) \\ y=y(u, v)\end{array}\right.
{x=x(u,v)y=y(u,v) 有连续偏导数,且满足
J
=
∂
(
x
,
y
)
∂
(
u
,
v
)
=
∣
x
u
y
u
x
v
y
v
∣
≠
0
J=\frac{\partial(x, y)}{\partial(u, v)}=\left|\begin{array}{ll} x_{u} & y_{u} \\ x_{v} & y_{v} \end{array}\right| \neq 0
J=∂(u,v)∂(x,y)=
xuxvyuyv
=0
而
f
(
x
,
y
)
∈
C
(
D
)
f(x, y) \in C(D)
f(x,y)∈C(D),那么
∬
D
f
(
x
,
y
)
d
x
d
y
=
∬
D
′
f
(
x
(
u
,
v
)
,
y
(
u
,
v
)
)
∣
J
∣
d
u
d
v
\iint \limits_{D} f(x, y) d x d y=\iint \limits_{D^{\prime}} f(x(u, v), y(u, v))|J| d u d v
D∬f(x,y)dxdy=D′∬f(x(u,v),y(u,v))∣J∣dudv
u
v
u v
uv 平面小矩形
A
′
B
′
C
′
D
′
⟶
x
y
A^{\prime} B^{\prime} C^{\prime} D^{\prime} \longrightarrow x y
A′B′C′D′⟶xy 平面曲边四边形
A
B
C
D
A B C D
ABCD
A
′
(
u
,
v
)
⟶
A
(
x
(
u
,
v
)
,
y
(
u
,
v
)
)
B
′
(
u
+
Δ
u
,
v
)
⟶
B
(
x
(
u
+
Δ
u
,
v
)
,
y
(
u
+
Δ
u
,
v
)
)
C
′
(
u
+
Δ
u
,
v
+
Δ
v
)
⟶
C
(
x
(
u
+
Δ
u
,
v
+
Δ
v
)
,
y
(
u
+
Δ
u
,
v
+
Δ
v
)
)
D
′
(
u
,
v
+
Δ
v
)
⟶
D
(
x
(
u
,
v
+
Δ
v
)
,
y
(
u
,
v
+
Δ
v
)
)
\begin{aligned} &A^{\prime}(u, v) \longrightarrow A(x(u, v), y(u, v)) \\ &B^{\prime}(u+\Delta u, v) \longrightarrow B(x(u+\Delta u, v), y(u+\Delta u, v)) \\ &C^{\prime}(u+\Delta u, v+\Delta v) \longrightarrow C(x(u+\Delta u, v+\Delta v), y(u+\Delta u, v+\Delta v)) \\ &D^{\prime}(u, v+\Delta v) \longrightarrow D(x(u, v+\Delta v), y(u, v+\Delta v)) \end{aligned}
A′(u,v)⟶A(x(u,v),y(u,v))B′(u+Δu,v)⟶B(x(u+Δu,v),y(u+Δu,v))C′(u+Δu,v+Δv)⟶C(x(u+Δu,v+Δv),y(u+Δu,v+Δv))D′(u,v+Δv)⟶D(x(u,v+Δv),y(u,v+Δv))
(此处应该有图)
A
B
C
D
ABCD
ABCD 近似平行四边形,只需求出一组邻边的向量表示
A
B
→
≈
(
x
u
(
u
,
v
)
Δ
u
,
y
u
(
u
,
v
)
Δ
u
)
A
D
→
≈
(
x
v
(
u
,
v
)
Δ
v
,
y
v
(
u
,
v
)
Δ
v
)
⇒
Δ
σ
≈
∣
x
u
(
u
,
v
)
Δ
u
x
v
(
u
,
v
)
Δ
u
y
u
(
u
,
v
)
Δ
v
y
v
(
u
,
v
)
Δ
v
∣
=
∣
J
∣
Δ
u
Δ
v
d
σ
=
∣
J
∣
d
u
d
v
\begin{aligned} & \overrightarrow{A B}\approx\left(x_{u}(u, v) \Delta u, y_{u}(u, v) \Delta u\right) \\ & \overrightarrow{A D}\approx\left(x_{v}(u, v) \Delta v, y_{v}(u, v) \Delta v\right) \\ & \Rightarrow\\ & \Delta \sigma \approx\left|\begin{array}{ll} x_{u}(u, v) \Delta u & x_{v}(u, v) \Delta u \\ y_{u}(u, v) \Delta v & y_{v}(u, v) \Delta v \end{array}\right| =|J| \Delta u \Delta v \\ \\ & d \sigma=|J| d u d v \end{aligned}
AB≈(xu(u,v)Δu,yu(u,v)Δu)AD≈(xv(u,v)Δv,yv(u,v)Δv)⇒Δσ≈
xu(u,v)Δuyu(u,v)Δvxv(u,v)Δuyv(u,v)Δv
=∣J∣ΔuΔvdσ=∣J∣dudv
第三节 三重积分
一、三重积分的定义
00 引入
∭ Ω f ( x , y , z ) d V \iiint_{\Omega} f(x, y, z) d V ∭Ωf(x,y,z)dV 你能说出它的含义吗?
概念联系的问题
一个占据三维空间中区域 Q Q Q 的几何体,其密度为 f ( x , y , z ) f(x,y,z) f(x,y,z),那么其质量为多少?
回顾定积分和二重积分的概念
求在三维区域上分布率非均匀的某种物理量 (或其它量) 的总量
分割—求和—求极限
01 定义
设 Ω \Omega Ω 是 R 3 R^{3} R3 中的有界闭区域,函数 f ( x , y , z ) f(x, y, z) f(x,y,z) 在 Ω \Omega Ω 上定义, I I I 为实数,
若将区域
Δ
Ω
1
,
Δ
Ω
2
,
⋯
,
Δ
Ω
n
\Delta \Omega_{1}, \Delta \Omega_{2}, \cdots, \Delta \Omega_{n}
ΔΩ1,ΔΩ2,⋯,ΔΩn,任取
(
ξ
i
,
η
i
,
ς
i
)
∈
Δ
Ω
i
\left(\xi_{i}, \eta_{i}, \varsigma_{i}\right) \in \Delta \Omega_{i}
(ξi,ηi,ςi)∈ΔΩi,作和
∑
i
=
1
n
f
(
ξ
i
,
η
i
,
ς
i
)
Δ
V
i
(
Δ
V
i
是
Δ
Ω
i
的体积
)
\sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}, \varsigma_{i}\right) \Delta V_{i}\quad(\Delta V_{i} 是 \Delta \Omega_{i} 的体积 )
i=1∑nf(ξi,ηi,ςi)ΔVi(ΔVi是ΔΩi的体积)
总有
lim
i
→
0
∑
i
=
1
n
f
(
ξ
i
,
η
i
,
ς
i
)
Δ
V
i
=
I
\lim _{i \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}, \varsigma_{i}\right) \Delta V_{i}=I
i→0limi=1∑nf(ξi,ηi,ςi)ΔVi=I
( 其中
λ
=
max
1
≤
i
≤
n
{
d
i
}
,
d
i
\lambda=\max _{1 \leq i \leq n}\left\{d_{i}\right\}, d_{i}
λ=max1≤i≤n{di},di 是小区域
Δ
Ω
i
\Delta \Omega_{i}
ΔΩi 的直径 )
则称函数
f
(
x
,
y
,
z
)
f(x, y, z)
f(x,y,z) 在
Ω
\Omega
Ω 可积,
I
I
I 称为
f
f
f 在
Ω
\Omega
Ω 的三重积分,记为
∭
Ω
f
(
x
,
y
,
z
)
d
V
(
d
V
−
体积元素
)
\iiint_{\Omega} f(x, y, z) d V\quad(dV-体积元素)
∭Ωf(x,y,z)dV(dV−体积元素)
02 意义
一种物理意义(三维物体的质量)
若 f ( x , y , z ) f(x,y,z) f(x,y,z) 表示占有三维空间区域 Q Q Q 的物体的质量密度函数,则
∭ Ω f ( x , y , z ) d V \iiint \limits_{\Omega} f(x, y, z) d V Ω∭f(x,y,z)dV 给出了物体的质量
02 性质
(1) 类似二重积分,有线性、可加性、单调性和中值定理,还有
(2) ∭ Ω 1 d V = V Ω ( Ω 的体积 ) \iiint \limits_{\Omega} 1 d V=V_{\Omega}\quad(\Omega的体积) Ω∭1dV=VΩ(Ω的体积)
二、在直角坐标系下的计算公式
直角坐标系下
∭
Ω
f
(
x
,
y
,
z
)
d
V
=
∭
Ω
f
(
x
,
y
,
z
)
d
x
d
y
d
z
\iiint \limits_{\Omega} f(x, y, z) d V=\iiint \limits_{\Omega} f(x, y, z) d x d y d z
Ω∭f(x,y,z)dV=Ω∭f(x,y,z)dxdydz
01 柱线法
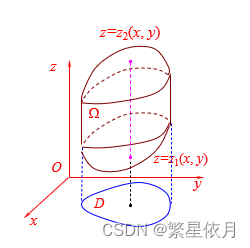
设 Ω \Omega Ω 是以曲面 z = z 1 ( x , y ) \mathrm{z}=\mathrm{z}_{1}(x, y) z=z1(x,y) 为底,曲面 z = z 2 ( x , y ) \mathrm{z}=\mathrm{z}_{2}(x, y) z=z2(x,y) 为顶,
而侧面是母线平行 z z z 轴的柱面所围成的区域。
设
Ω
\Omega
Ω 在
x
y
x y
xy 平面上的投影区域为
D
D
D ,则
Ω
\Omega
Ω 可表示为(
x
y
x y
xy 型正则区域)
{
(
x
,
y
,
z
)
∣
z
1
(
x
,
y
)
≤
z
≤
z
2
(
x
,
y
)
,
(
x
,
y
)
∈
D
}
\left\{(x, y, z) \mid z_{1}(x, y) \leq z \leq z_{2}(x, y),(x, y) \in D\right\}
{(x,y,z)∣z1(x,y)≤z≤z2(x,y),(x,y)∈D}
从质量角度求三重积分,则
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z) 为密度,对
(
x
,
y
)
∈
D
(x,y)\in D
(x,y)∈D,
μ
(
x
,
y
)
=
∫
z
1
(
x
,
y
)
z
2
(
x
,
y
)
f
(
x
,
y
,
z
)
d
z
\mu(x, y)=\int_{z_{1}(x, y)}^{z_{2}(x, y)} f(x, y, z) d z
μ(x,y)=∫z1(x,y)z2(x,y)f(x,y,z)dz
给出了
Ω
\Omega
Ω 内由
z
1
(
x
,
y
)
z_1(x,y)
z1(x,y) 到
z
2
(
x
,
y
)
z_2(x,y)
z2(x,y) 的线段上所分布的质量密度。
物体的总质量就是
∬
D
(
∫
z
1
(
x
,
y
)
z
2
(
x
,
y
)
f
(
x
,
y
.
z
)
d
z
)
d
x
d
y
\iint \limits_{D}\left(\int_{z_{1}(x, y)}^{z_{2}(x, y)} f(x, y . z) d z\right) d x d y
D∬(∫z1(x,y)z2(x,y)f(x,y.z)dz)dxdy
从而
∭
Ω
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∬
D
d
x
d
y
∫
z
1
(
x
,
y
)
z
2
(
x
,
y
)
f
(
x
,
y
⋅
z
)
d
z
\iiint \limits_{\Omega} f(x, y, z) d x d y d z=\iint \limits_{D} d x d y \int_{z_{1}(x, y)}^{z_{2}(x, y)} f(x, y \cdot z) d z
Ω∭f(x,y,z)dxdydz=D∬dxdy∫z1(x,y)z2(x,y)f(x,y⋅z)dz
02 截面法
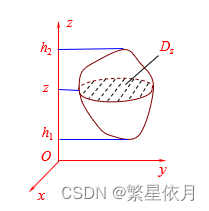
设区域 Ω \Omega Ω 在 z z z 轴上投影区间为 [ h 1 , h 2 ] [h_{1}, h_{2}] [h1,h2],即 Ω \Omega Ω 介于平面 z = h 1 \mathrm{z}=h_{1} z=h1 与 z = h 2 \mathrm{z}=h_{2} z=h2 之间,
垂直
z
z
z 轴过
z
z
z 处的平面截
Ω
\Omega
Ω 所得截面为区域
D
z
D_z
Dz,则(
z
z
z 型空间区域)
Ω
=
{
(
x
,
y
,
z
)
∣
(
x
,
y
)
∈
D
z
,
h
1
≤
z
≤
h
2
}
\Omega=\left\{(x, y, z) \mid(x, y) \in D_{z}, h_{1} \leq z \leq h_{2}\right\}
Ω={(x,y,z)∣(x,y)∈Dz,h1≤z≤h2}
仍从质量角度考虑,对
z
∈
[
h
1
,
h
2
]
z\in[h_1,h_2]
z∈[h1,h2],二重积分
F
(
z
)
=
∬
D
z
f
(
x
,
y
,
z
)
d
x
d
y
F(z)=\iint \limits_{D_{z}} f(x, y, z) d x d y
F(z)=Dz∬f(x,y,z)dxdy
给出了物体在截面
D
z
D_z
Dz 上所分布的质量。物体的总质量为:
∫
z
1
z
2
(
∬
D
z
f
(
x
,
y
,
z
)
d
x
d
y
)
d
z
\int_{z_{1}}^{z_{2}}\left(\iint \limits_{D_{z}} f(x, y, z) d x d y\right) d z
∫z1z2
Dz∬f(x,y,z)dxdy
dz
从而有:
∭
Ω
f
(
x
,
y
,
z
)
d
V
=
∫
h
1
h
2
d
z
∬
D
x
f
(
x
,
y
,
z
)
d
x
d
y
\iiint \limits_{\Omega} f(x, y, z) d V=\int_{h_{1}}^{h_{2}} d z \iint \limits_{D_{x}} f(x, y, z) d x d y
Ω∭f(x,y,z)dV=∫h1h2dzDx∬f(x,y,z)dxdy
三、三重积分变量代换
与二重积分的变量代换类似,
设变换
{
x
=
x
(
u
,
v
,
w
)
y
=
y
(
u
,
v
,
w
)
z
=
z
(
u
,
v
,
w
)
\left\{\begin{array}{l} x=x(u, v, w) \\ y=y(u, v, w) \\ z=z(u, v, w) \end{array}\right.
⎩
⎨
⎧x=x(u,v,w)y=y(u,v,w)z=z(u,v,w) 有连续偏导数,且满足
J
=
∂
(
x
,
y
,
z
)
∂
(
u
,
v
,
w
)
=
∣
x
u
y
u
z
u
x
v
y
v
z
v
x
w
y
w
z
w
∣
≠
0
J=\frac{\partial(x, y, z)}{\partial(u, v, w)}=\left|\begin{array}{lll} x_{u} & y_{u} & z_{u} \\ x_{v} & y_{v} & z_{v} \\ x_{w} & y_{w} & z_{w} \end{array}\right| \neq 0
J=∂(u,v,w)∂(x,y,z)=
xuxvxwyuyvywzuzvzw
=0
而
f
(
x
,
y
,
x
)
∈
C
(
Ω
)
f(x,y,x)\in C(\Omega)
f(x,y,x)∈C(Ω),那么
∭
Ω
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∭
Ω
f
(
x
(
u
,
v
,
w
)
,
y
(
u
,
v
,
w
)
,
z
(
u
,
v
,
w
)
)
∣
J
∣
d
u
d
v
d
w
\iiint \limits_{\Omega} f(x, y, z) d x d y d z=\iiint \limits_{\Omega} f(x(u, v, w), y(u, v, w), z(u, v, w))|J| d u d v d w
Ω∭f(x,y,z)dxdydz=Ω∭f(x(u,v,w),y(u,v,w),z(u,v,w))∣J∣dudvdw
01 柱面坐标系下的三重积分
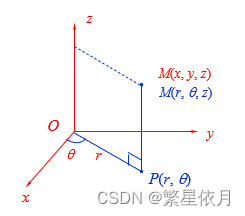
这个坐标系实际上就是 x y xy xy 坐标转变为极坐标,即变换公式为 { x = r cos θ y = r sin θ z = z \left\{\begin{array}{c}x=r \cos \theta \\ y=r \sin \theta \\ z=z\end{array}\right. ⎩ ⎨ ⎧x=rcosθy=rsinθz=z
由于
∂
(
x
,
y
,
z
)
∂
(
r
,
θ
,
z
)
=
∣
cos
θ
sin
θ
0
−
r
sin
θ
r
cos
θ
0
0
0
1
∣
=
r
\frac{\partial(x, y, z)}{\partial(r, \theta, z)}=\left|\begin{array}{ccc} \cos \theta & \sin \theta & 0 \\ -r \sin \theta & r \cos \theta & 0 \\ 0 & 0 & 1 \end{array}\right|=r
∂(r,θ,z)∂(x,y,z)=
cosθ−rsinθ0sinθrcosθ0001
=r
得到柱坐标积分公式
∭
Ω
f
(
x
,
y
,
z
)
d
V
=
∭
Ω
f
(
r
cos
θ
,
r
sin
θ
,
z
)
r
d
r
d
θ
d
z
\iiint \limits_{\Omega} f(x, y, z) d V=\iiint \limits_{\Omega} f(r \cos \theta, r \sin \theta, z) r d r d \theta d z
Ω∭f(x,y,z)dV=Ω∭f(rcosθ,rsinθ,z)rdrdθdz
注意,事实上,在具体计算时,可以用柱线法或截面法得到
D
D
D ( 或
D
z
D_z
Dz ) 的二重积分,再转化为极坐标。
02 球面坐标系下的三重积分

设点 M ( x , y , z ) M(x, y, z) M(x,y,z) 是空间一点,引进球坐标 ( ρ , φ , θ ) (\rho, \varphi, \theta) (ρ,φ,θ)
ρ = ∥ O M → ∥ \rho=\|\overrightarrow{O M}\| ρ=∥OM∥, φ : O M → \varphi: \overrightarrow{O M} φ:OM 与z轴正向的夹角, θ : O P → \theta: \overrightarrow{O P} θ:OP 与 x x x 轴正向的夹角,
且
ρ
\rho
ρ,
φ
\varphi
φ,
θ
\theta
θ 满足
0
≤
ρ
≤
+
∞
,
0
≤
φ
≤
π
,
0
≤
θ
≤
2
π
或
−
π
≤
θ
≤
π
0 \leq \rho \leq+\infty\ \ ,\ \ 0 \leq \varphi \leq \pi\ \ ,\ \ 0 \leq \theta \leq 2 \pi\ 或-\pi\leq\theta\leq\pi
0≤ρ≤+∞ , 0≤φ≤π , 0≤θ≤2π 或−π≤θ≤π
坐标变换关系式
⟹
{
x
=
ρ
sin
φ
cos
θ
y
=
ρ
sin
φ
sin
θ
z
=
ρ
cos
φ
\quad\Longrightarrow\ \left\{\begin{array}{c} x=\rho \sin \varphi \cos \theta \\ y=\rho \sin \varphi \sin \theta \\ z=\rho \cos \varphi \end{array}\right.
⟹ ⎩
⎨
⎧x=ρsinφcosθy=ρsinφsinθz=ρcosφ
由于雅可比行列式
∂
(
x
,
y
,
z
)
∂
(
ρ
,
φ
,
θ
)
=
∣
sin
φ
cos
θ
sin
φ
sin
θ
cos
φ
ρ
cos
φ
cos
θ
ρ
cos
φ
sin
θ
−
ρ
sin
φ
−
ρ
sin
φ
sin
θ
ρ
sin
φ
cos
θ
0
∣
=
ρ
2
sin
φ
\begin{aligned} \frac{\partial(x, y, z)}{\partial(\rho, \varphi, \theta)} &=\left|\begin{array}{ccc} \sin \varphi \cos \theta & \sin \varphi \sin \theta & \cos \varphi \\ \rho \cos \varphi \cos \theta & \rho \cos \varphi \sin \theta & -\rho \sin \varphi \\ -\rho \sin \varphi \sin \theta & \rho \sin \varphi \cos \theta & 0 \end{array}\right| =\rho^{2} \sin \varphi \end{aligned}
∂(ρ,φ,θ)∂(x,y,z)=
sinφcosθρcosφcosθ−ρsinφsinθsinφsinθρcosφsinθρsinφcosθcosφ−ρsinφ0
=ρ2sinφ
导出
∭
Ω
f
(
x
,
y
,
z
)
d
V
=
∭
Ω
∗
f
(
ρ
sin
φ
cos
θ
,
ρ
sin
φ
sin
θ
,
ρ
cos
φ
)
ρ
2
sin
φ
d
ρ
d
φ
d
θ
\begin{aligned} & \iiint \limits_{\Omega} f(x, y, z) d V =\iiint \limits_{\Omega^{*}} f(\rho \sin \varphi \cos \theta, \rho \sin \varphi \sin \theta, \rho \cos \varphi) \rho^{2} \sin \varphi d \rho d \varphi d \theta \end{aligned}
Ω∭f(x,y,z)dV=Ω∗∭f(ρsinφcosθ,ρsinφsinθ,ρcosφ)ρ2sinφdρdφdθ
使用球坐标时,
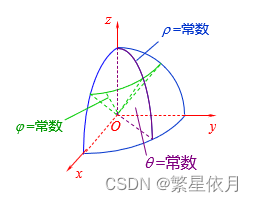
ρ = \rho= ρ= 常数:球面, φ = \varphi= φ= 常数: 锥面, θ = \theta= θ= 常数: 平面,
且球面和锥面的中心在原点,平面过 z z z 轴。
注意,围成区域的部分曲面有上述特点,或被积函数含 x 2 + y 2 + z 2 x^{2}+y^{2}+z^{2} x2+y2+z2,可考虑用球坐标
第四节 重积分的应用
一、曲面面积

设空间曲面 S S S 为 z = f ( x , y ) z=f(x,y) z=f(x,y), ( x , y ) (x,y) (x,y) 定义于 D D D,即曲面 S S S 在 x y xy xy 平面的投影区域为 D D D,如何求 S S S 的面积?
用分割求和(微元法)的思想将 D D D 分割成小区域,对应 D D D 上小区域面积 Δ σ = Δ x Δ y \Delta \sigma=\Delta x \Delta y Δσ=ΔxΔy , S S S 上的小曲面面积为 Δ S \Delta S ΔS,当小区域微小时, Δ S ∣ cos φ ∣ ≈ Δ σ \Delta S|\cos \varphi| \approx \Delta \sigma ΔS∣cosφ∣≈Δσ,其中 φ \varphi φ 是 Δ S \Delta S ΔS 所在平面与 x y xy xy 平面夹角。

φ \varphi φ 是 Δ S \Delta S ΔS 上的法向量与 z z z 方向的夹角,这两个方向向量分别为 { z x , z y , − 1 } , { 0 , 0 , 1 } \left\{z_{x}, z_{y},-1\right\},\{0,0,1\} {zx,zy,−1},{0,0,1}
导出
∣
cos
φ
∣
=
1
1
+
z
x
2
+
z
y
2
|\cos \varphi|=\frac{1}{\sqrt{1+z_{x}^{2}+z_{y}^{2}}}
∣cosφ∣=1+zx2+zy21
因此得到曲面面积的有关公式
d
S
=
1
+
z
x
2
+
z
y
2
d
x
d
y
(
曲面面积元素
)
S
=
∬
D
1
+
z
x
2
+
z
y
2
d
x
d
y
\begin{aligned} &d S=\sqrt{1+z_{x}^{2}+z_{y}^{2}} d x d y \ \ \ (曲面面积元素)\\ &S=\iint \limits_{D} \sqrt{1+z_{x}^{2}+z_{y}^{2}} d x d y \end{aligned}
dS=1+zx2+zy2dxdy (曲面面积元素)S=D∬1+zx2+zy2dxdy
二、重积分的物理应用举例
01 质心
物体的质心 ( 或重心 ) 与它的质量和静力矩有关。
设面密度为 μ ( x , y ) \mu(x, y) μ(x,y) 薄板占据平面区域 D D D
考虑 D D D 上面积元素 d x d y d x d y dxdy 其质量为 μ ( x , y ) d x d y \mu(x, y) d x d y μ(x,y)dxdy,
从而对 y y y 轴的静力矩为 d M y = x μ ( x , y ) d x d y d M_{y}=x \mu(x, y) d x d y dMy=xμ(x,y)dxdy
质量 m m m 和静力矩 M y M_{y} My 为: m = ∬ D μ ( x , y ) d σ m=\iint \limits_{D} \mu(x, y) d \sigma m=D∬μ(x,y)dσ, M y = ∬ D x μ ( x , y ) d σ M_{y}=\iint \limits_{D} x \mu(x, y) d \sigma My=D∬xμ(x,y)dσ
同样,对 x x x 轴电静力矩 M x = ∬ D y μ ( x , y ) d σ M_{x}=\iint \limits_{D} y \mu(x, y) d \sigma Mx=D∬yμ(x,y)dσ
于是薄片的质心位置
(
x
ˉ
,
y
ˉ
)
(\bar{x}, \bar{y})
(xˉ,yˉ)
x
ˉ
=
M
y
m
=
∬
D
x
μ
(
x
,
y
)
d
σ
∬
D
μ
(
x
,
y
)
d
σ
,
y
ˉ
=
M
x
m
=
∬
D
y
μ
(
x
,
y
)
d
σ
∬
D
μ
(
x
,
y
)
d
σ
\bar{x}=\frac{M_{y}}{m}=\frac{\iint \limits_{D} x \mu(x, y) d \sigma}{\iint \limits_{D} \mu(x, y) d \sigma}, \quad \bar{y}=\frac{M_{x}}{m}=\frac{\iint \limits_{D} y \mu(x, y) d \sigma}{\iint \limits_{D} \mu(x, y) d \sigma}
xˉ=mMy=D∬μ(x,y)dσD∬xμ(x,y)dσ,yˉ=mMx=D∬μ(x,y)dσD∬yμ(x,y)dσ
注意,当
μ
=
1
\mu=1
μ=1 时得到平面图形的形心
思考:对三维物体如何求质心。
02 转动惯量
转动惯量也是一种矩 ( 二次矩 ),设平面区域 D D D 上薄板的面密度为 μ ( x , y ) \mu(x,y) μ(x,y) ,
那么面积元素
d
σ
d \sigma
dσ 处微量物体对
y
y
y 轴的转动惯量
d
I
y
=
x
2
μ
(
x
,
y
)
d
σ
⟹
I
y
=
∬
D
x
2
ρ
(
x
,
y
)
d
σ
\begin{aligned} & d I_{y}=x^{2} \mu(x, y) d \sigma \quad \Longrightarrow \quad I_{y}=\iint \limits_{D} x^{2} \rho(x, y) d \sigma \end{aligned}
dIy=x2μ(x,y)dσ⟹Iy=D∬x2ρ(x,y)dσ
问题:对
x
x
x 轴和对原点
O
O
O 的转动惯量?
最后
😊为防止河蟹,链接已经通过“与熊论道/熊曰加密”加密处理,将下面的文字复制到“与熊论道/熊曰加密”页面的第二个输入框,点击“领悟熊所言的真谛”即可查看链接啦:
😊熊曰:呋食食和嚁非象嗚家吃呱山萌萌笨有哞魚既魚性蜜覺呆食哮性洞哮山噗眠嗥嚄萌洞擊嗄襲呱物人你
😊如果嫌麻烦的话请私信咨询博主,谢谢!
😊PS:繁星依月/惟欢/一舟均为博主的马甲,本篇作品完全原创,再次感谢!





















 1542
1542











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








