【mmseg配置解析-3】 Polynomial Decay 多项式衰减

mmseg配置解析 Polynomial Decay 多项式衰减

B站：肆十二-的个人空间-肆十二-个人主页-哔哩哔哩视频 (bilibili.com)

博客：肆十二-CSDN博客

问答：(10 封私信 / 72 条消息) 肆十二 - 知乎 (zhihu.com)

Polynomial Decay（多项式衰减）是一种常用于深度学习中学习率调度的方法。在训练过程中，学习率从初始值逐步减少到一个最小值（eta_min），以帮助模型更好地收敛到最优解。Polynomial Decay 的衰减过程遵循一个多项式函数，其公式如下：

Polynomial Decay 公式

如果我们设定初始学习率为 lr_initial，最小学习率为 eta_min，训练的总步数为 max_iters，当前的步数为 current_iter，衰减的指数为 power，那么 Polynomial Decay 的学习率 lr 可以表示为：

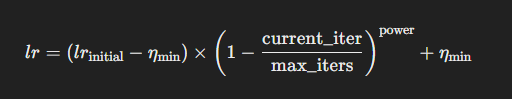
参数解释

• lr_initial：初始学习率，训练开始时的学习率。
• eta_min：最小学习率，训练结束时的学习率。
• current_iter：当前的迭代次数。
• max_iters：总迭代次数，训练的总步数。
• power：多项式的幂次，控制衰减曲线的形状。power 越大，学习率衰减越慢；power 越小，学习率衰减越快。

举例说明

假设我们有以下参数：

• 初始学习率 lr_initial = 0.1
• 最小学习率 eta_min = 0.001
• 总迭代次数 max_iters = 1000
• 当前迭代次数 current_iter = 500
• 衰减指数 power = 2 （表示二次衰减）

根据上述公式，学习率 lr 可以计算为：
$$lr=(0.1-0.001)\times (1-5001000)2+0.001lr=(0.1-0.001)\times {\left(1-\frac{500}{1000}\right)}^2+0.001lr=(0.1-0.001)\times (1-1000500)2+0.001$$
首先计算衰减因子：
$$(1-5001000)=0.5\left(1-\frac{500}{1000}\right)=0.5(1-1000500)=0.5$$
然后计算其平方（因为 power = 2）：

0.52=0.250.5^2 = 0.250.52=0.25

接着代入公式计算当前的学习率：
$$lr=(0.1-0.001)\times 0.25+0.001lr=(0.1-0.001)\times 0.25+0.001lr=(0.1-0.001)\times 0.25+0.001lr=0.099\times 0.25+0.001=0.02475+0.001=0.02575lr=0.099\times 0.25+0.001=0.02475+0.001=0.02575lr=0.099\times 0.25+0.001=0.02475+0.001=0.02575$$
所以在第 500 次迭代时，学习率将下降到 0.02575。

学习率曲线

如果绘制 Polynomial Decay 的学习率曲线，随着训练迭代的增加，学习率会从初始值平滑地减小到最小值。power 的大小会影响曲线的形状：

• power=1：线性衰减。
• power>1：衰减速度较慢，曲线开始时下降较快，但接近最小值时变化缓慢。
• power<1：衰减速度较快，曲线开始时下降缓慢，但接近最小值时变化较快。

何时使用

Polynomial Decay 通常用于需要平滑降低学习率的场景，特别是在训练的最后阶段，模型需要更小的学习率来微调参数，以避免过大的梯度更新导致损失函数的不稳定。

这种方法在深度学习的很多任务中都有应用，特别是在训练大规模模型或需要长时间训练的任务中，它能帮助模型在早期迅速收敛并在后期细致调整，获得更好的性能。