K-D Tree 算法详解及Python实现

K-D Tree 算法

　　$\mathrm{k-d\ tree}$即$\mathrm{k-dimensional\ tree}$，是一种分割k维数据空间的数据结构，常用来多维空间关键数据的搜索(如：范围搜素及近邻搜索)，是二叉空间划分树的一个特例。通常，对于维度为$k$，数据点数为$N$的数据集，$\mathrm{k-d\ tree}$适用于$N \gg 2^k$的情形。

k-d tree算法原理

　　为了避免比较生硬苦涩的文字说明，这里我采用简单的例子表明$\mathrm{k-d\ tree}$算法。假设有6个二维数据点$\left \{ (2,3),(5,4),(9,6),(4,7),(8,1),(7,2)\right \}$数据点位于二维空间内(如图1所示)。k-d树算法就是要确定图1中这些分割空间的分割线(多维空间即为分割平面，一般为超平面)。下面就要通过一步步展示k-d树是如何确定这些分割线的。

图1 二维数据k-d树空间划分示意图
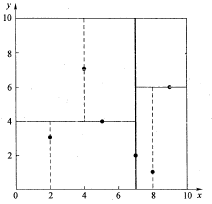
　　 $\mathrm{k-d\ tree}$算法可以分为两大部分，一部分是有关k-d树本身这种数据结构建立的算法，另一部分是在建立的k-d树上如何进行最邻近查找的算法。

k-d树构建算法

　　首先列出构建k-d树的伪代码见表1，其中k-d树每个节点中主要包含的数据结构见表2。(参考于王永明 王贵锦 编著的《图像局部不变特性特征与描述》)

表1 构建k-d树的伪码

算法：构建k-d树（createKDTree）
输入：数据点集Data-set和其所在的空间Range
输出： Kd，类型为Kd-tree
1 If Data-set 是空的，则返回空的 Kd-tree
2 调用节点生成程序： 　　（1）确定split域：对于所有描述子数据（特征矢量），统计它们在每个维上的数据方差。以SURF特征为例，描述子为64维，可计算64个方差。挑选出最大值，对应的维就是split域的值。数据方差大表明沿该坐标轴方向上的数据分散得比较开，在这个方向上进行数据分割有较好的分辨率； 　　(2）确定Node-data域：数据点集Data-set按其第split域的值排序。位于正中间的那个数据点被选为Node-data。此时新的Data-set’ = Data-set\Node-data（除去其中Node-data这一点）。
3 　　dataleft = {d属于Data-set’ && d[split] ≤ Node-data[split]} 　　Left_Range = {Range && dataleft} 　　dataright = {d属于Data-set’ && d[split] > Node-data[split]} 　　Right_Range = {Range && dataright}
4 left = 由（dataleft，Left_Range）建立的k-d tree，即递归调用createKDTree（dataleft，Left_ Range）。并设置left的parent域为Kd； right = 由（dataright，Right_Range）建立的k-d tree，即调用createKDTree（dataleft，Left_ Range）。并设置right的parent域为Kd。

表2 k-d树中每个节点的数据类型

域名	数据类型	描述
Node-data	数据矢量	数据集中某个数据点，是n维矢量（这里也就是k维）
Range	空间矢量	该节点所代表的空间范围
split	整数	垂直于分割超平面的方向轴序号
Left	k-d树	由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
Right	k-d树	由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
parent	k-d树	父节点

以上述举的实例来看，过程如下：

　　由于此例简单，数据维度只有2维，所以可以简单地给$x，y$两个方向轴编号为$0,1$，也即split=$\left \{0,1\right\}$。
　　（1）确定split域的首先该取的值。分别计算$x，y$方向上数据的方差得知$x$方向上的方差最大，所以split域值首先取$0$，也就是$x$轴方向；
　　（2）确定Node-data的域值。根据