螺旋线拟合

实验坐标是这样的

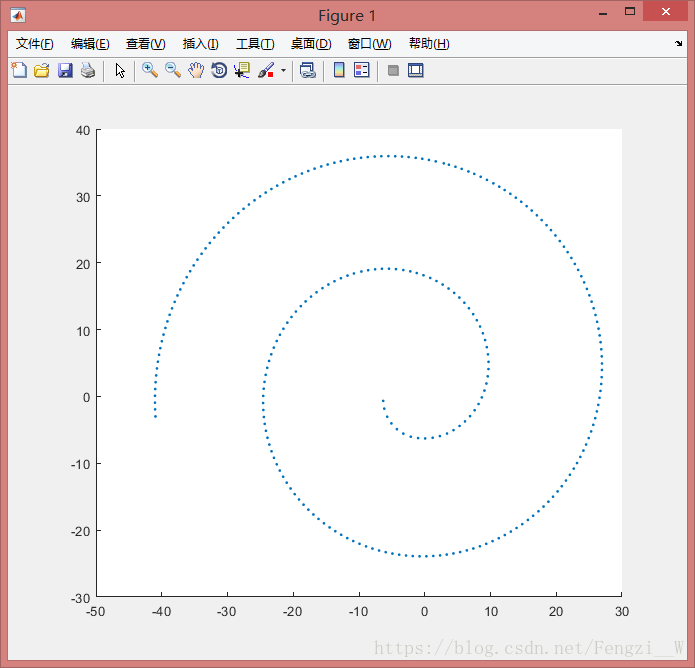
基本是一个阿基米德螺旋线，原数据是笛卡尔坐标系的，通过拟合半径与方位角之间的关系得到多项式

以下是多项式拟合

clc
clear
format long
shuju=xlsread('jingpan12')
x=flipud(shuju(:,1));
y=flipud(shuju(:,2));
r=sqrt(x.^2+y.^2);
jiaodu=acosd(x./r);
for i=1:1:19
    jiaodu(i)=360-jiaodu(i);
end
for i=20:1:73
    jiaodu(i)=360+jiaodu(i);
end
for i=74:1:147
    jiaodu(i)=720-jiaodu(i);
end
for i=148:1:254
    jiaodu(i)=720+jiaodu(i);
end
for i=255:1:257
    jiaodu(i)=1080-jiaodu(i);
end
jiaodu=jiaodu*3.14./180;
plot(jiaodu,r);
p9=polyfit(jiaodu,r,9);
n=3.2:0.1:16;
y9=polyval(p9,n,'.');
hold on
plot(n,y9)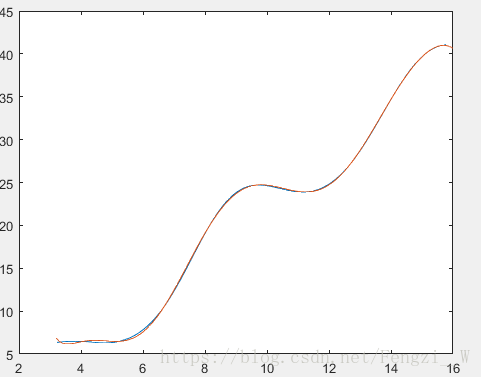

拟合结果

将数据回代，

clear all
clc
format long
shuju=xlsread('jingpan12')
p=[-5.00630375898308e-06,0.000460742305865134,-0.0182267190094672,0.404815073833663,-5.53480697324230,48.0789047375280,-264.371215185261,886.259566745230,-1645.21576472083,1297.95181501538]
for n=3.2:0.1:16;
p9=polyval(p,n);
c=p9*cos(n);
d=p9*sin(n);
plot(c,d,'.')
hold on
end
plot(shuju(:,1),shuju(:,2),'.')

回代结果

实线是元数据，点是拟合结果