强化学习学习笔记（3）---贝尔曼最优公式

小齿轮|

已于 2024-05-15 18:22:24 修改

阅读量1.7k

点赞数 17

分类专栏：强化学习文章标签：学习笔记

于 2024-05-14 15:56:19 首次发布

本文链接：https://blog.csdn.net/Fourglsl/article/details/138840868

版权

强化学习专栏收录该内容

3 篇文章

订阅专栏

本章主要内容

关键概念：最优状态值（optimal state value）和最优策略（ optimal policy）；
函数工具：贝尔曼最优方程（the Bellman optimality equation (BOE)）

一、激励性例子（Motivating examples）

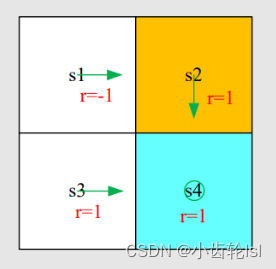
第一步：根据实例写出每个状态对应的贝尔曼方程：

第二步：求每个状态对应的状态值（state value），假定这里的 $\gamma$ =0.9，先由第四个式子求s4的状态值（state value），再求s1,s2,s3的状态值（state value）：

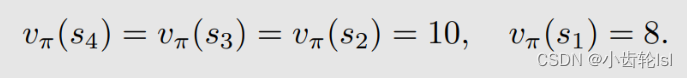
第三步：根据上一步求出的状态值（state value），再求出动作值（action value），这里以s1状态为例，求s1状态时各个动作的动作值（action value），每一个状态都有5个可采取的动作，故有相应的5个动作值（action value）,而每一个动作action也对应着一个策略和状态值（state value）：

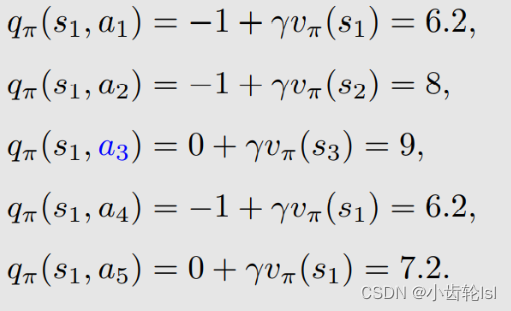
总结：从上述求解得到的动作值（action value）可知，在采取动作a3的时候值是最大的，因此这个策略也是最优的。采取动作a3的时候值是最大的原因是s3状态是一个可进入的网格。

改进：在上述例子中，可以看到在s1状态的时候，当前的策略是：

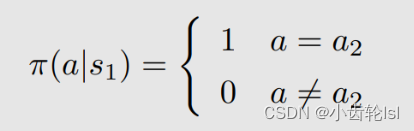
通过在第二步和第三步对状态值（state value）和动作值（action value）求解并对比之后可知，在s1状态时，采取动作a3的策略是最优的，因此我们选择一个新的策略（式子中的 $a^{*}$ 就是得到最优策略的动作，在本例中是a3）：

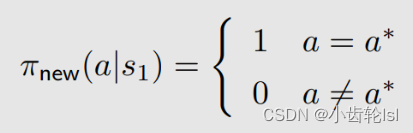
总结：

动作值（action value）就是评估动作的主要参数，如果选择一个动作action之后，它对应的动作值action value很大，那么证明可以得到更多的reward，相应的策略也更好；
在计算过程中，利用不断地迭代，就可以得到一个最优策略。就是首先对每个状态都选择 action value 最大的 action，选择完了一次，然后再来一次迭代得到一个新的策略，再迭代得到一个新的策略，最后那个策略一定会趋向一个最优的策略。

二、最优策略（Optimal policy）

状态值（state value）是评估一个策略是否最优，如果有一个策略，它的状态值比在这个状态所有其他策略的状态值都要大，那么这个策略就是最优策略：

三、贝尔曼最优方程（Bellman optimality equation (BOE)）

贝尔曼最优方程：
方程中p(r|s, a), p(s'|s, a) 已知；v(s), v(s‘)未知要计算得到；π(s) 未知（贝尔曼公式依赖于一个给定的 π，而贝尔曼最优公式的 π 没有给定，需要求解）。

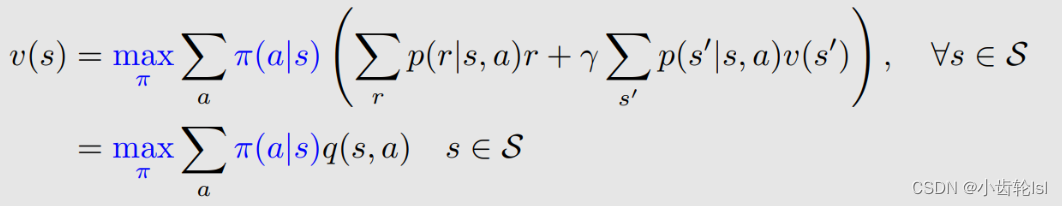
贝尔曼最优方程的矩阵向量形式Bellman optimality equation (matrix-vector form)：

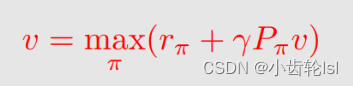
公式右边两个元素的推导式如下，在第二章中有推导：

总结：

贝尔曼方程描述了最优策略和最优状态值state value；
贝尔曼公式的π(a|s) 是给定已知的，依赖于一个给定的 π；
在贝尔曼公式前面加上了 max_π成为贝尔曼最优公式，这时候 π 就不再是给定的了，因为这里面嵌套了一个优化问题，需要先解决这个优化问题求解出这个 π，再把这个 π 带到这个式子里面去，求解出状态值。

四、贝尔曼最优方程右侧的最大值（Maximization on the right-hand side of BOE）

先看贝尔曼最有方程，如果右侧有最大值，那么最优策略也相应的求出：

右侧的最大值求解思路

贝尔曼最优方程中，有一个式子，却有两个未知量（状态值 v 和策略 π，对任意一个状态都要求出来最优的一个 π）。

第一步

在下边的简单例子中，如果想要使2x-1-a2的值最大，显然当a=0的时候有最大值；这时方程消除a后是x=2x-1，计算得x=1，即当x=1，的时候方程有解。

照着这个思路可以总结出：

最初的方程中已知与未知的值：p(r|s, a), p(s’ |s, a), r, γ 已知；v(s), v(s‘ ) 未知；π(s) 未知；
固定 v(s') 并求解 π，即给出 v(s') 的一个初始值，把初始值给定后，v(s') 变成已知的，第一行的大括号内部写成 q(s,a)，是已知的。下面要做的是把 π(a|s) 确定下来；
这里有多个 action，在网格世界中有 5 个 a，q(s, a1)，q(s, a2)，q(s, a3)，q(s, a4)，q(s, a5)。

列式子：

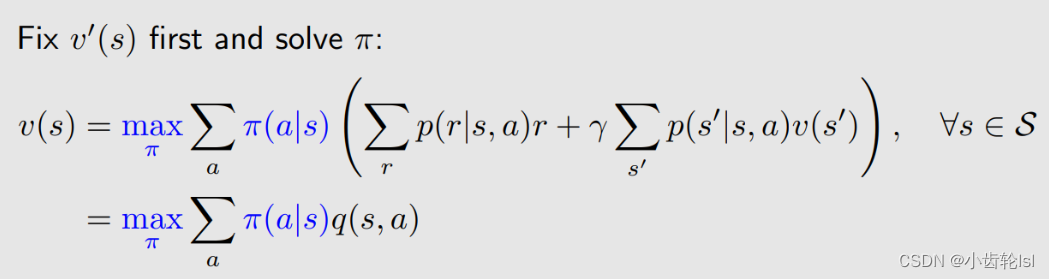
第二步

为了求解π(a|s) ，再给出一个例子，假如已知三个 q 值，要解决的问题是求解三个系数或者叫三个权重，使得下面的目标函数（object function）达到最大；
系数和权重应该满足和为 1 ，并且每个值都大于等于 0，之所以有这样的约束，是因为这个例子里面的系数对应上面的概率 π(a|s) ，概率 π 满足这样的性质；
假设 q3 是最大的，最优解是 c3* = 1，c1*=c2*=0；

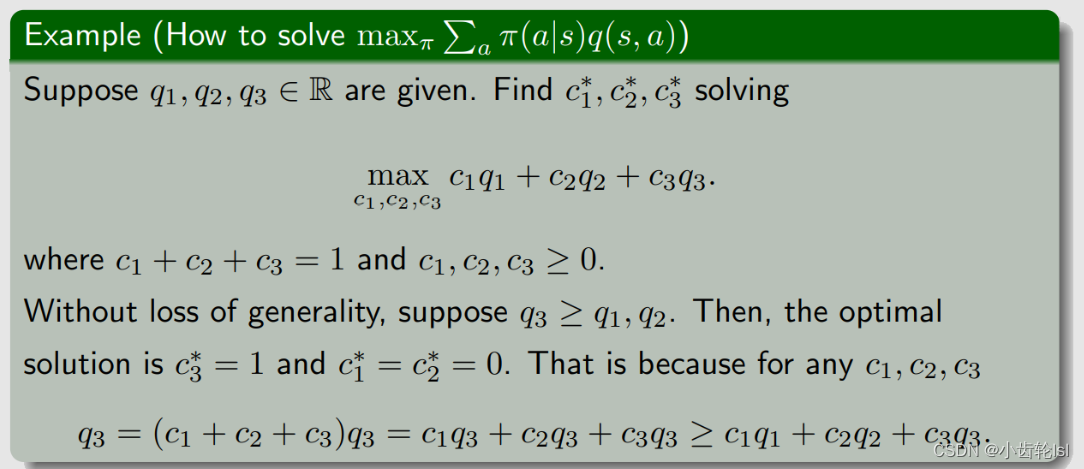
照着这个思路可以总结出：

通过上面的例子，我们就知道了如果右边的 q(s,a) 确定了，如何求解最优的 π(a|s)，最后的结果就是右边这一项的最优值等于最大的 q(s,a) 值，这里 π(a|s) 的选取应该是对于 a* 等于 1，不是 a* 等于 0，这里 a* 对应最大的 q 值的 action，即 q(s，a*) 是所有 v 的取值里最大的。

五、贝尔曼最优公式的求解（Solve the Bellman optimality equation）

把等式右侧写成一个函数 f(v)，之所以这样是因为求解等式右侧最大值 max_π 的方法是先固定 v ，就可以求出一个 π，至于这个 π 是什么样子，最后得到的最优值是什么不用太关心，我们知道右侧肯定是 v 的一个函数。本来右侧是 π 和 v 的函数，现在把 π 确定下来了，右侧就变成了 v 的函数（与上面第一个例子一样）

对每一个v，都能求出一个max，这个max是和v有关的式子。那么把v看成变量，max就是v的函数了，把这个函数定义成f(v)；
π 是 v 的函数，老师说了，所以右边整体都是v的函数；
冒号等号代表定义的意思；
其实就是分两步，第一步求max, 消掉Π; 第二步求出v；
其实就是Π已知了，要开始求最大的state value；
贝尔曼方程实际上是一组方程，对每一个状态都有一个贝尔曼方程；
和选取的动作的概率无关，因为取最大值适合概率是1，所以只需要考虑v的值；
参考前面向量形式的展开，这里f(v)第s个元素对应的是s下的最大v(s)。

优化后的贝尔曼公式：

下面我们求解贝尔曼最优公式就求解 v = f(v) 即可。

六、收缩映射定理（Preliminaries: Contraction mapping theorem）

1.收缩映射定理（Preliminaries: Contraction mapping theorem）定义

不动点（Fixed point）：点 x 属于集合 X，f 是一个映射（或者叫函数），如果满足 f(x) = x，则 x 就被称为一个不动点。

收缩映射Contraction mapping（或收缩函数contractive function）（mapping 和 function其实是一回事）：f 是收缩映射（contraction mapping），如果满足：（伽马可以自由选择的，只要在0到1之间）

下边是一个说明解释的例子：

Contraction mapping theorem定理：

对于任何形式为 x = f(x) 的方程，如果 f 是收缩映射，那么满足

存在性：存在一个满足 f(x*) = x* 的不动点（fixed point） x*。我们不太关心 f 的表达式究竟是什么，只要它是一个 Contraction mapping，就一定存在一个不动点（fixed point）满足 f(x*) = x*；
唯一性：不动点（fixed point） x* 是唯一存在的；
算法（求解这样的一个不动点（fixed point）的算法）：考虑一个序列 {xk}，其中 xk+1 = f(xk) （迭代算法），则当 k → ∞ 时， xk → x*（即 xk 会收敛到 x*）。此外，收敛速度是指数级的，非常快。（先给一个 x0，x1=f(x0) 求出 x1；再用 x2=f(x1)求出 x2，以此类推，求出的 xk 会收敛到 x*）

2.例子

通过收缩映射定理和迭代算法来求解

七、贝尔曼最优公式的收缩特性（Contraction property of BOE）

1.推导过程

让我们再回到贝尔曼最优方程：v = f(v)，这个就是 Contraction mapping 要解决的那一类问题：

为了应用 Contraction mapping theorem ，我们首先要证明贝尔曼最优公式里面的 f(v) 是一个 Contraction mapping：

我们知道了 f(v) 是一个 Contraction mapping，那么贝尔曼最优公式就可以立刻用收缩映射定理（Contraction mapping theorem）来求解出来，可以得到以下结果：

在这个贝尔曼最优公式的收缩性质下，我们可以计算得到总是存在一个解V*，且这个解是唯一的；这个解可以通过迭代算法来求解得出（迭代的原理就是，先给定一个猜测的V0，然后逐渐迭代收敛，最后得到的Vk就收敛于V*，这个迭代收敛速度很快，并且取决于γ值）

下面详细解析一下由 Contraction mapping theorem 给出的迭代算法：

迭代算法矩阵向量形式（Matrix-vector form）：

化成元素形式（Elementwise form）：即对于某一个具体的 s 状态这个算法是怎么运行的：

总结：

对任意状态 s，即当前我们对解 v*(s) 有一个估计，这个估计是 v_k(s)，最开始可以是 v_0(s)，这个可以是任意的一个值；
对任意状态 s 下的每一个 action，求解 q_k(s,a) ， v_k(s’) 是刚才第一步给定的；
计算 s 的贪婪策略 πk+1 如下：基于 q_k(s,a) 我们得到一个新的策略，这个策略是 π_k+1(a|s) 会选择最大的 q_k(s,a) 对应的 a_k*（与第五部分思想一样）；
计算 v_k+1(s) = max_a q_k(s, a) ；
下边算法实际上就是下一讲中讨论的值迭代算法（value iteration algorithm），这个算法其实计算由 Contraction mapping theorem 给出来的算法。

2.例子

动作：a_l、a_0、a_r 代表向左走、保持不变、向右走。
奖励：进入目标区域： +1；尝试走出边界：-1；其他：0

q(s, a) 的值（建立 q-value 的一个表 table）（这里的 q 是第五部分那个非常长的一串可以缩写成这样的一个 q；
q-value 其实可以理解为state value的一个action下的值，这里的 q-value 就是 action value。

我们的目标是找到 v*(s_i) 和 π*（此时我们还没有将 v* 和 π*究竟是什么，我们只知道它是能够求解出贝尔曼最优公式对应的值和策略，之后我们会知道它们就是最优的状态值 state value 和最优的策略）

初始化v空间->找到各s处使v最大的a（得到policy）->更新v，重复

这个策略已经不错了，画出图后发现可以到达目标状态，已经达到了最优策略，但是 v 还没有达到贝尔曼最优公式的最优的解，所以还要继续迭代算下去，在考虑下一个 interation

可以无限迭代下去，如果要编程实现，可以写一个迭代终止条件，两者之差若小于一个很小的数字，我们任务再去迭代也没什么太大变化了，可以停下，认为 v_k 达到了贝尔曼最优公式的解

八、贝尔曼最优公式最优策略（Policy optimality）

假设 v* 是贝尔曼最优方程（BOE）的解，可以用刚才介绍的算法求解出来。它满足：

假设：

π* 是对应 v* 的一个最优的策略，也就是把 v* 固定住，可以求解出来一个 π ，这个 π 我们用 π* 来表示，那么把公式 2 代入公式 1，公式 1 可以化成下面的式子，也就是把前面的 max_π 去掉了，把它改成了 π*

上面的公式 3 其实就是一个贝尔曼公式，因为贝尔曼公式一定是对应一个策略，那么上式就是对应 π* 的一个贝尔曼公式，这里的 v* = v_ π*，也就是 π* 对应的 state value，所以贝尔曼最优公式是一个特殊的贝尔曼公式，贝尔曼最优公式中对应的策略比较特殊，是一个最优的策略。

对于贝尔曼最优公式的解 v*，它是最大的 state value，对于任何一个其他的策略（policy）π，所得到的状态值（state value）v_ π 都没有 v* 大。那么相应的 π* 肯定是一个最优的策略，因为 π* 所对应的 v* 就是 v_ π*，它对应的 state value 达到最大。

现在我们明白为什么要研究贝尔曼最优公式（BOE）了。这是因为它描述了最优状态值（optimal state value）和最优策略（optimal policy）。

那么 π* 长什么样子？之前讲过，我们应该不陌生，也就是在状态 s 的时候 π* 会选择 a*，也就是在状态 s 对应的 action value 最大的那个 action，对这个 action 概率是 1，对其他 action 概率是 0.所以它是确定性 deterministic 的，也是贪婪 greedy 的，就是不论什么，反正就选择最大的。

九、.分析最优策略（Analyzing optimal policies）

从下面的贝尔曼最优公式（BOE）可以清晰地看到：

我们要做的是求出黑色字体的变量，它们分别对应了最优的策略和最优的 state value ；我们已知的是这些红色字体的变量，它们分别对应了概率，这个概率就代表了系统的模型；r 是我们设计的奖励（reward）；γ 是折扣因子。

求解贝尔曼最优公式就是在已知红色的量的时候求出黑色的量，那么显然最优的策略和最优的 state value 就是由这些红色的量来决定：他们分别是怎么设计 r，怎么选择 γ，还有系统模型是什么样的

接下来，我们用实例来说明当我们改变 r 和 γ 的时候，最优策略会发生什么样的改变（因为系统模型一般很难改变，所以我们不考虑这个）。

例子

通过求解贝尔曼最优公式（BOE），可以得到最优策略（左图绿色箭头）和相应的最优状态值（state value）（右图格子上的数字）。观察最优策略可以看出，最优策略没有绕开禁区（forbidden area），因为它发现进入禁区虽然暂时得到一个负数的惩罚，但是从长远来看我进入禁区到达目标所得到的回报（return）比绕一大圈再到达目标获得的回报（return）更大。最优策略敢于冒险：进入禁区！！

如果我们将 γ = 0.9 改为 γ = 0.5（其他参数不变，即设计的奖励 r 不变），由左图绿色箭头可以看出，最优策略已经发生改变，(a) 的最优策略是进入禁区到达目标，而 (b) 的最优策略是绕一大圈到达目标，因为它衡量发现绕一大圈再到达目标获得的回报（return）比进入禁区到达目标所得到的回报（return）更大。最优策略变得目光短浅！避开所有禁区！

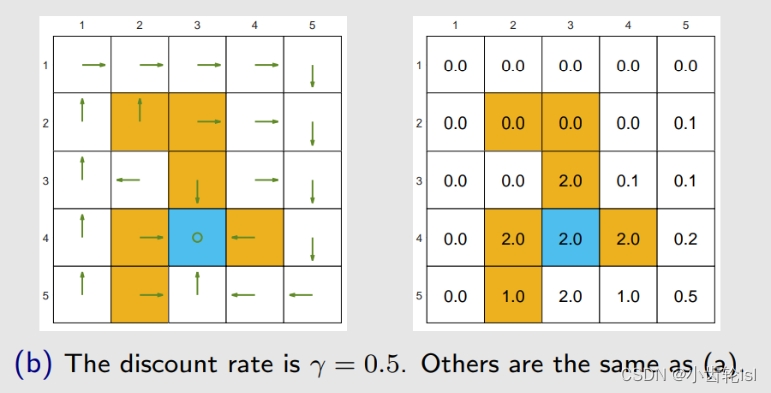
总结：

之所以这样是因为当 γ 比较大的时候，智能体比较远视，它会比较重视未来的 reward；当 γ 比较小的时候，智能体比较近视，return 里所得到的值的大小主要由近期所得到的 reward 来决定， γ 比较小它的幂次方就小，未来的 reward 会被打折的很厉害。

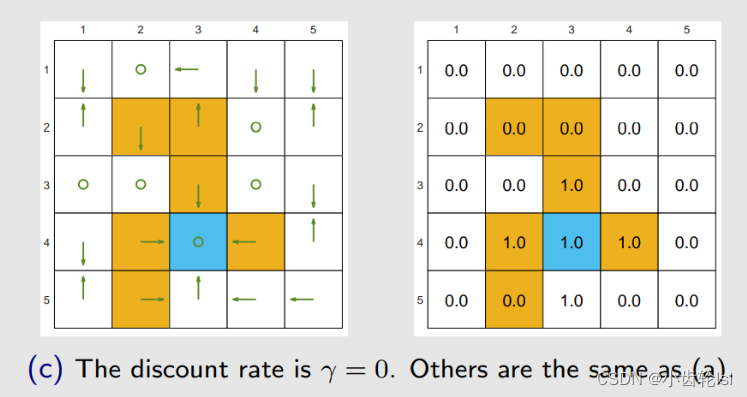
如果我们将 γ 改为 0。最优策略变得极其短视！同时，只选择即时奖励（immediate reward）最大的动作！从很多状态出发根本无法达到目标！

如果我们在进入禁区时加大惩罚力度（γ = 0.9），最优策略也绕开了禁区。
最优策略保持不变！因为重要的不是奖励（reward）的绝对值（absolute reward values）！而是它们的相对值（relative values）！

举例

毫无意义的绕行？

通过求解贝尔曼最优公式可以得到图 (a) 左图的最优策略（绿色箭头）和右图的最优状态值（optimal state value），(a) 中的策略是最优的，(b) 中的策略不是。

问题：为什么最优策略不是（b）？为什么最优策略不走毫无意义的弯路？我们定义从一个白色格子到另一个白色格子的 r=0，即走弯路不会受到惩罚。那么为什么最优策略不走毫无意义的弯路？

答案：因为折扣因子 γ

自己的理解就是随着这一次没有惩罚，但是随着尝试次数变多，discount rate<1，后边获得相应的奖励就会变少。

总结：

由上面的例子得到的启发：在设计 reward 的时候，很多人可能会觉得每走一步应该给一个惩罚 r=-1，r=-1 代表能量的消耗，这样它就不会绕远路，就会尽可能走最短的路径到达目标，如果 r=0，没有 r=-1 好像就会绕远路，其实不是这样的，因为除了 r 来约束它不要绕远路之外，还有 γ，因为越绕远路我们得到到达目标的奖励越晚，越晚那时候对应的 γ 的次方越小，奖励打折会很厉害，所有它自然会找一个最短的路径过去。

十、总结

有关贝尔曼最优方程的问题：

存在性：这个方程有解吗？
有，根据收缩映射定理
唯一性：这个方程的解是否唯一？
是，根据收缩映射定理（最优状态值 optimal state value 这个解是唯一的，但是对应 optimal state value 的最优策略 π 不一定是唯一的）
算法：如何求解这个方程，如何求解最优策略和最优解？
根据收缩映射定理提出的迭代算法
最优性：我们为什么要研究这个方程
因为贝尔曼最优公式的解对应于最优状态值（state value）和最优策略（opyimal policy）
最后，我们明白了研究BOE的重要性！