再看CNN中的卷积

最新推荐文章于 2024-09-22 22:29:57 发布
最新推荐文章于 2024-09-22 22:29:57 发布
阅读量7.4k 收藏 9
点赞数
分类专栏： Deep learning 文章标签： cnn 卷积 全卷积
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Gavin__Zhou/article/details/72723494
版权

这两天在看CS231n的课程笔记，结合着原版英文和知乎上中文版翻译在看，确实Andrej Karpathy写的很棒，很多都是些实践经验不仅仅是理论知识. 我结合着自己的理解和Karpathy的介绍，重新看确实又收获了不少，以前觉得不明白的地方现在也清晰了，所以重新写这个再看篇，仅供参考

CNN的组成

  • convolution layer
  • pooling layer
  • fc layer
  • Batch Normalization layer

基础的三大部件(卷积, 池化, 全连接)，最近两年Residual learning的流行导致大量的用到Batch Norm layer，此外还有像激活函数(Relu, PRelu, tanh等), LRU等.
我的工作中大量使用到的是Kaiming等人提出的Residual的形式，现今直接stack三大部件是很少见的，因为会出现像梯度消失等的问题. 不了解的直接去看相关的论文吧，推荐两篇:

(1) Residual Learning
(2) Wide Residual

基本的实现就是Residual Block.

细说卷积

卷积是CNN的重心，也是这篇博客的重点.

CNN的卖点

我的个人理解是两个卖点:

  1. 局部连接
  2. 参数共享

局部连接

对待像图像这样的高维数据，直接让神经元与前一层的所有神经元进行全连接是不现实的，这样做的害处显而易见: 参数过多，根本无法计算.
所以我们让每个神经元只与输入数据的一个局部区域连接，这个局部区域的大小就是局部感受野(receptive field)，尺寸上等同于filter的空间尺寸(比如5*5*3).
为何说局部连接是CNN的卖点呢？通过局部连接的方式避免了参数的爆炸式增长(对比全连接的方式). 通过下面的参数共享可以大大的缩减实际的参数量，为训练一个多层的CNN提供了可能.

参数共享

这里直接上案例，来的更加直观.
先给出计算公式:
ouput_width = (input_width-filter_width+2*padding)/stride+1

现给出如下假设:

input: 227*227*3(height, width, channel)
filter: 96个11*11的filter，strider=4, padding=0

我们可以算出output的shape是(55,55,96).

假设是全连接的方式，意味着需要:

神经元总数是: 55*55*96=290400
每个神经元连接的参数是: 11*11*3+1=364(+1表示bias)
总共参数的个数是: 290400*364=105705600，差不多1亿个参数!!!
这还只是一层(一般我们说网络的层数是不算输入层的)，假设是10层呢，自己想想吧.

所以我们需要参数共享.

参数共享的方式下:
不是每个神经元都有11*11*3，而是每个filter控制的实际大小(55*55)共享这个filter的参数，故此时的参数总共是:

(11*11*3+1)*96=34944，可以看到此时的参数相比于全连接减少非常多.

说的太通俗了，大家可以看知乎上的翻译，说的很好，我只是按照自己的理解来说.

图示

conv

看图示其实很明白了，input(7*7*3)，2个filter(3*3, stride=2, pad=0). input的pad=1，所以5*5 -> 7*7. 由此可见filter的shape其实是(height, width, inChannel, outChannel)，在这里就是(3,3,3,2).

Tensorflow中的conv2d的API:

conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None,
data_format=None, name=None)
filter: A Tensor. Must have the same type as input. A 4-D tensor of shape [filter_height, filter_width, in_channels, out_channels]

实现

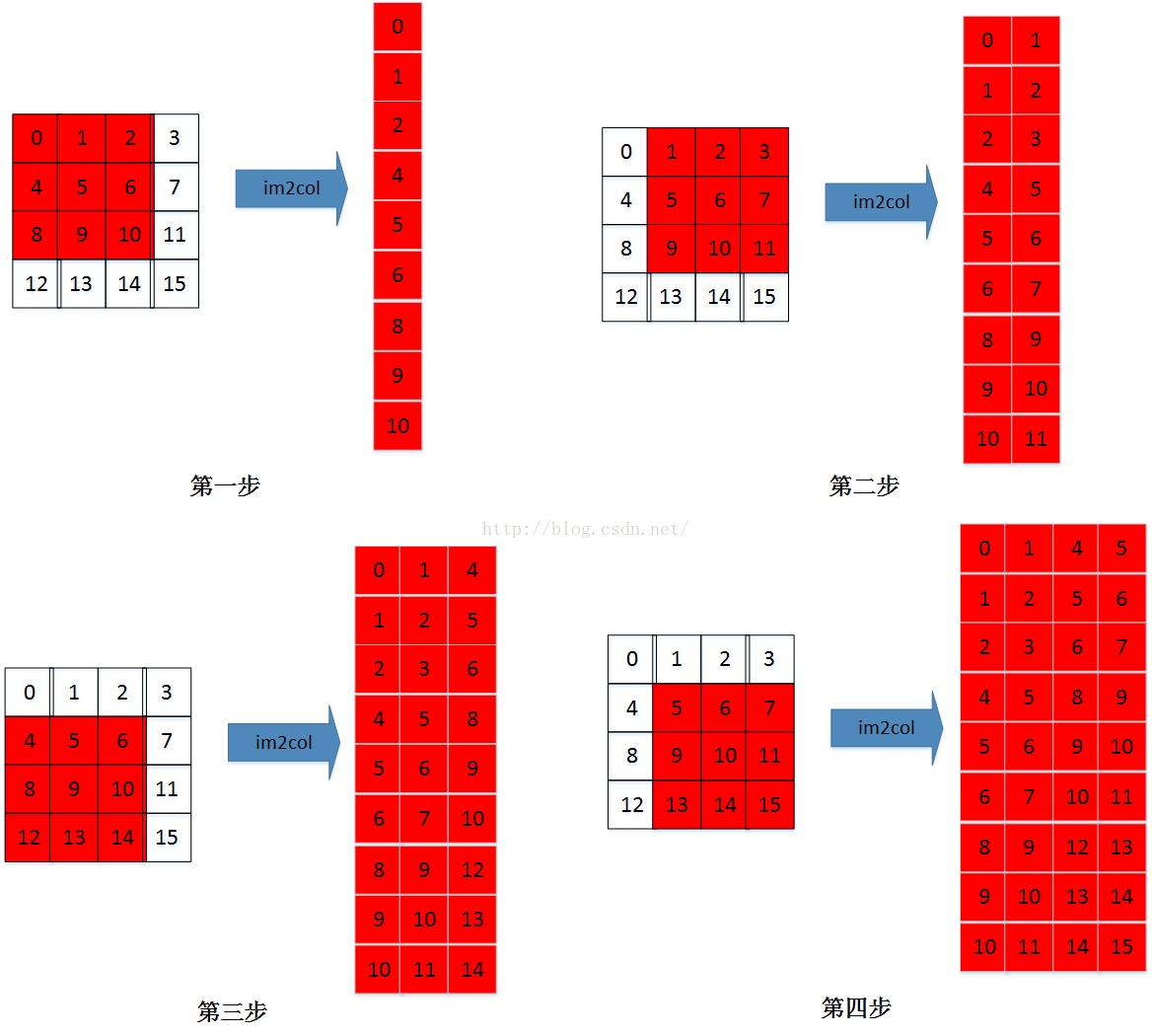
卷积运算本质上就是在滤波器和输入数据的局部区域间做点积，所以可以用矩阵乘法来实现. 当然可以用一个类似于划窗那样的方式去实现，但是考虑到实现效率一般都是用im2col的方式实现，这样可以高效的利用优化之后的矩阵乘法，具体可以参考Caffe中的im2col的实现.

Karpathy的解释方式是多通道的im2col，有可能比较抽象，所以咱们还是从单个channel看起吧.
假设input(4*4*3), filter(3*3*3*6, stride=1, pad=0)

现在只看一个channel的情况:

single_channel

多(3)个channel的情况:
多个channel的im2col的过程就是顺序im2col多个channel，首先im2col第一通道，然后在im2col第二通道，最后im2col第三通道，…

现在看下karpathy的总结就很清楚了:

im2col

1*1的卷积

用的也挺多的，Residual和Inception的实现里面就有用1*1卷积的.

resiudal_with_1*1

inception_module

作用是两个:

  • 实现跨通道(cross-channel)的交互和信息整合
  • 进行卷积核通道数的降维和升维，减少网络参数

可以参考知乎上的回答，最早的论文是Network in Network这篇，地址戳我

全卷积

我最早接触到全卷积是用在Semantic Segmentation的FCN上，火了之后全卷积用在了很多地方，比如用于Object Detection的RFCN.

Caffe上有将fc layer转换为全卷积的示例: net-surgery

原理上来说将fc转换为全卷积挺简单的:
(1) 假设input(5*5*16)，fc1(4096), fc2(1000)
(2) 可以把fc1看成是(1*1*4096)，fc2同理

你只需要用5*5*16*4096的filter去和input卷积就可以得到(1*1*4096)这就是fc1，fc1和1*1*4096*1000的filter去卷积就可以得到(1*1*1000)也就是fc2了.

将fc转换为全卷积的高效体现在下面的场景上:

让卷积网络在一张更大的输入图片上滑动，得到多个输出，这样的转化可以让我们在单个向前传播的过程中完成上述的操作.

这里原文引用知乎上的翻译:

举个例子，如果我们想让224x224尺寸的浮窗，以步长为32在384x384的图片上滑动，把每个经停的位置都带入卷积网络，最后得到6x6个位置的类别得分。上述的把全连接层转换成卷积层的做法会更简便。如果224x224的输入图片经过卷积层和汇聚层之后得到了[7x7x512]的数组，那么，384x384的大图片直接经过同样的卷积层和汇聚层之后会得到[12x12x512]的数组（因为途径5个汇聚层，尺寸变为384/2/2/2/2/2 = 12）。然后再经过上面由3个全连接层转化得到的3个卷积层，最终得到[6x6x1000]的输出（因为(12 - 7)/1 + 1 = 6）。这个结果正是浮窗在原图经停的6x6个位置的得分!
面对384x384的图像，让（含全连接层）的初始卷积神经网络以32像素的步长独立对图像中的224x224块进行多次评价，其效果和使用把全连接层变换为卷积层后的卷积神经网络进行一次前向传播是一样的。

dilated convolution

dilated在原始的convolution上加了个rate参数，导致卷积的时候会skip rate-1个像素.

It performs convolution with holes, sampling the input values every rate pixels in the height and width dimensions. This is equivalent to convolving the input with a set of upsampled filters, produced by inserting rate - 1 zeros between two consecutive values of the filters along the height and width dimensions.

图示如下:

dilated convolution

在不增加参数的情况下，增大filter的感受野(receptive field).

It also allows us to effectively enlarge the field of view of filters without increasing the number of parameters or the amount of computation.

基本用在dense predictive的场景中:

  1. Detection of fine-details by processing inputs in higher resolutions.
  2. Broader view of the input to capture more contextual information.
  3. Faster run-time with less parameters

Tensorflow有API直接调用: atrous_conv2d

总结

总结下重点内容:
1. 参数共享
2. 卷积实现
3. 1*1卷积
4. 全卷积

参考

  1. 知乎上的cs231n中文翻译
  2. dilated-convolution的介绍
  3. 1*1卷积作用知乎上的回答
  4. 神经网络能够拟合任意函数的解释
GavinZhou_xd
关注
专栏目录
【深度学习】最强算法之：卷积神经网络（CNN）
商务合作 | 面试培训 | 职场规划 ==>主页扫码
03-22 4956
深度学习必会算法之：卷积神经网络
cnn卷积神经网络PPT详解
08-11
作为一名 IT 行业大师，我将详细解释 CNN 卷积神经网络的知识点，涵盖标题、描述、标签和部分内容中的相关信息。 卷积神经网络（CNN） 卷积神经网络（Convolutional Neural Networks，CNN）是一种深度学习算法，...
CNN(卷积神经网络)详解
热门推荐
nwnlp的博客
02-26 32万+
Why CNN 首先回答这样一个问题，为什么我们要学CNN，或者说CNN为什么在很多领域收获成功？还是先拿MNIST来当例子说。MNIST数据结构不清楚的话自行百度。。 我自己实验用两个hidden layer的DNN(全连接深度神经网络)在MNIST上也能取得不错的成绩(98.29%)。下面是一个三个hidden layer的网络结构图 盗图1 全连接深度神经网络，顾名思义，每个神经...
CNN卷积神经网络的原理与实践
最新发布
qq_61600833的博客
09-22 1126
卷积神经网络（CNN）是深度学习领域中的一种重要网络结构，广泛应用于图像识别、目标检测和自然语言处理等领域。本文将详细介绍CNN的基本原理、关键组成部分，并通过一个简单的实例来展示如何构建一个卷积神经网络。'''定义神经网络'''self.conv1 = nn.Sequential( #将多个层组合在一起nn.Conv2d(in_channels=1, # 图像通道个数，1表示灰度图out_channels=16, # 要得到几个特征图，卷积核的个数。
CNN（卷积神经网络）
u014299761的博客
04-25 555
CNN（卷积神经网络）整理 一般神经网络有三个操作——卷积、池化、全连接，全连接一般在最后一层，保证不管输入的维度如何变化，它的输出是统一的，有3个核心——卷积核、激活函数、池化，常见池化有最大池化、均值池化。 卷积：个人理解为局部的加权求和，卷积核即为同层卷积的权值，感受野（接受域）间参数共享。卷积核移动时有一个步长，也就是步幅stride，一般是1——卷积核在输入上的移动间距是1。 从概...
卷积神经网络（CNN）
Flaneur-yz的博客
08-16 2491
前言 CNN，即卷积神经网络，主要用于图像识别，分类。由输入层，卷积层，池化层，全连接层(Affline层），Softmax层叠加而成。卷积神经网络中还有一个非常重要的结构:过滤器，它作用于层与层之间(卷积层与池化层），决定了怎样对数据进行卷积和池化。 一、卷积神经网络的网络结构 卷积神经网络主要由这几类层构成：输入层、卷积层，ReLU层、池化（Pooling）层和全连接层（全连接层和常规神经网络...
一文读懂卷积神经网络CNN（学习笔记）
数据派THU
12-29 5198
来源：机器学习算法与自然语言处理作者：白雪峰本文为图文结合，建议阅读10分钟。本文为大家解读如何简单明了的解释卷积，并且分享了学习中的一些方法案例。首先文章的提纲为：CNN栗子镇楼What is CNN            什么是卷积            什么是池化Why CNN对CNN的其他一些理解CNN实现（接口）1、CNN栗子（A Beginning Glimpse of CNN）Mod
cnn卷积神经网络cnn卷积神经网络cnn卷积神经网络cnn卷积神经网络.txt
05-22
cnn卷积神经网络cnn卷积神经网络cnn卷积神经网络cnn卷积神经网络cnn卷积神经网络
基于CNN(卷积神经网络）实现缺陷检测案例
06-10
基于CNN(卷积神经网络）实现缺陷检测案例基于CNN(卷积神经网络）实现缺陷检测案例基于CNN(卷积神经网络）实现缺陷检测案例基于CNN(卷积神经网络）实现缺陷检测案例基于CNN(卷积神经网络）实现缺陷检测案例基于CNN...
CNN_卷积神经网络MATLAB_
10-04
本资料包“CNN_卷积神经网络MATLAB_”提供了一个可运行的CNN模型示例，旨在帮助用户了解和掌握在MATLAB环境中搭建和应用CNN的方法。 CNN的核心组件包括卷积层、池化层、全连接层和激活函数等。卷积层是CNN的基石，...
时序预测 - MATLAB实现CNN(卷积神经网络)时间序列预测（完整源码和数据）
05-25
在本文中，我们将深入探讨如何使用MATLAB实现卷积神经网络（CNN）进行时间序列预测。这个主题结合了深度学习和时间序列分析两大领域，对于处理具有时间依赖性的数据非常有用，例如金融市场、气象预测、电力消耗等。...
机器学习-卷积神经网络（CNN）
qq_42538588的博客
08-15 2657
交叉熵损失用于评估预测概率分布与实际标签分布之间的差异。对于一个多分类问题，交叉熵损失 ( L ) 的定义为：( C ) 是类别数。( y_i ) 是实际标签的指示函数。如果样本属于第 ( i ) 类，则 ( y_i = 1 )，否则为 ( 0 )。( \hat{y}_i ) 是模型对第 ( i ) 类的预测概率。均方误差 ( L ) 定义为：( N ) 是样本数量。( y_j ) 是真实值。( \hat{y}_j ) 是预测值。
CNN卷积计算
qianchenghaozi的博客
12-05 382
卷积计算公式，假设输入图片和卷积核均为正方形尺寸分别为x,y：z=x-y/stride+1 经过pooling层,尺寸为d, 则输出尺寸为z/d
Computer Vision中的卷积神经网络(CNN)（基础篇）
SunshineSki的博客
11-01 5877
文章目录引言边缘检测Padding卷积步长（Strided Convolutions）三维卷积单层卷积网络（One layer of a convolutional network）小测试：一个简单卷积网络参数的计算池化层（Pooling Layers）卷积神经网络示例 （Convolutional neural network example）为什么使用卷积？（Why convolutions?...
机器学习之卷积神经网络--CNN介绍
qq_46556714的博客
06-15 5837
卷积神经网络（Convolutional Neural Networks，CNN）是一种包 含卷积计算且具有深度结构的前馈神经网络，是深度学习的代表算法之一。 常见的CNN网络有LeNet-5、VGGNet、GoogleNet、ResNet、 DenseNet、MobileNet等。 CNN主要应用场景： 图像分类、图像分割 、 目标检测 、 自然语言处 理等领域。CNN基本结构：INPUT -> 卷积->激活 -> 池化 -> 全连接 ->OUTPUT对输入的图像数据与卷积核做卷积运算提取图像的高阶特征
CNN卷积方式汇总
Share的博客
08-04 262
1. 原始版本 最早的卷积方式还没有任何骚套路，那就也没什么好说的了。见下图，原始的 conv 操作可以看做一个 2D 版本的无隐层神经网络。 附上一个卷积详细流程：【TensorFlow】tf.nn.conv2d 是怎样实现卷积的？ - CSDN 博客 2. 多隐层非线性版本 这个版本是一个较大的改进，融合了 Network In Network 的增加隐层提升非线性表达的思想，于是有了这种先用 1*1 的卷积映射到隐空间，再在隐空间做卷积的结构。同时考虑了多尺度，在单层卷积层中用多个不同大小的.
三万字硬核详解：卷积神经网络CNN（原理详解 + 项目实战 + 经验分享）
shinuone的博客
10-31 1万+
深入解析卷积神经网络（CNN）的实际应用，全面整理并梳理了CNN的关键知识点。从基础概念到实战技巧，加速理解与实战，并解决实际问题。
卷积神经网络Convolutional-Neural-Networks(CNN)理论概述
FPGA/MATLAB学习教程/源码/项目合作开发
03-21 2354
C1层中各平面（由神经元构成）提取图像中不同的局部特征，如边缘特征，上下左右方向特征等，C1层中的输入是有由上一层局部窗口的数值和连接的权值的加权和（也就是卷积，后面会具体解释为什么是卷积），然后通过一个激活函数（如sigmoid 函数，反正切函数）得到C1层的输出，接下来S2层是下采样层，简单来书，由4个点下采样为1个点，也就是4个数的加权平均。看下图2，假设红色的点和黑色的点是C1层第一个特征图的2个不同神经元，感受窗口的大小是5*5的（意味着有25个连接），这2个神经元连接的权值是共享的（相同的）。
卷积神经网络中的部分问题
songyimin1208的博客
04-03 1万+
转载来自：http://blog.csdn.net/maweifei/article/details/52443995 步幅和填充 好了，现在来看一下我们的卷积神经网络。还记得过滤器、感受野和卷积吗？很好。现在，要改变每一层的行为，有两个主要参数是我们可以调整的。选择了过滤器的尺寸以后，我们还需要选择步幅（stride）和填充（padding）。 步幅控制着过滤器围绕输入
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值