深度学习基础：一致性的评价方法（皮尔森相关系数法、Cohen‘s Kappa相关系数）

一致性的评价方法主要用于衡量不同变量、评价者或方法之间的关联性或可靠性。以下针对皮尔森相关系数法（Pearson Correlation Coefficient）和Cohen’s Kappa相关系数的核心原理、应用场景及差异进行详解：

1 什么是一致性评价

2 一致性评价（皮尔森相关系数法）

1. 核心原理

皮尔森相关系数衡量两个连续变量之间的线性相关程度，其公式为：
$$r=\frac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum (x_i-\bar{x}{)}^2}\sqrt{\sum (y_i-\bar{y}{)}^2}}$$
取值范围为**[-1, 1]**：

• 1：完全正相关
• -1：完全负相关
• 0：无线性相关

2. 应用场景

• 用户兴趣一致性：例如分析两个用户对商品的评分相似性。
• 预测值与真实值的相关性：验证模型预测结果与实际结果的匹配程度。
• 连续变量分析：如身高与体重、收入与消费等连续型数据的关联性研究。

3. 适用条件

• 变量需服从正态分布。
• 数据需满足线性关系假设。
• 异常值敏感性强，极端值可能显著影响结果。

4. 局限性

• 仅反映线性关系，无法捕捉非线性关联（如二次函数关系）。
• 对数据分布要求严格，非正态数据需改用Spearman或Kendall秩相关。

---

3 一致性评价（Cohen’s Kappa 相关系数）

1. 核心原理

Cohen’s Kappa用于评估两个评价者对同一组分类数据的一致性，其公式为：
$$\kappa =\frac{P_a-P_e}{1-P_e}$$

• $P_a$：观察一致性（实际一致的比例）。
• $P_e$：期望一致性（随机情况下预期一致的比例）。
  取值范围为**[-1, 1]**，通常解释为：
• $<0$：一致性比随机更差
• $0.6\sim 0.8$：中等一致性
• $>0.8$：高度一致性

2. 应用场景

• 医学诊断：两位医生对患者疾病分类的一致性评价。
• 问卷调查：不同评分者对同一问题的分类结果一致性。
• 机器学习：模型分类结果与人工标注的匹配度评估。

3. 优势

• 考虑随机因素：比简单一致率（如准确率）更可靠，避免高一致率的假象。
• 适用于离散分类：尤其适合名义尺度（如阴性/阳性）或有序分类（如轻度/中度/重度）。

4. 局限性

• 类别不平衡敏感：若某一类别占比过高，可能低估一致性（即“Kappa悖论”）。
• 需配合显著性检验（如Z检验）判断结果是否统计显著。

---

4 Cohen’s Kappa计算方法

5 Cohen’s Kappa取值的一致性含义

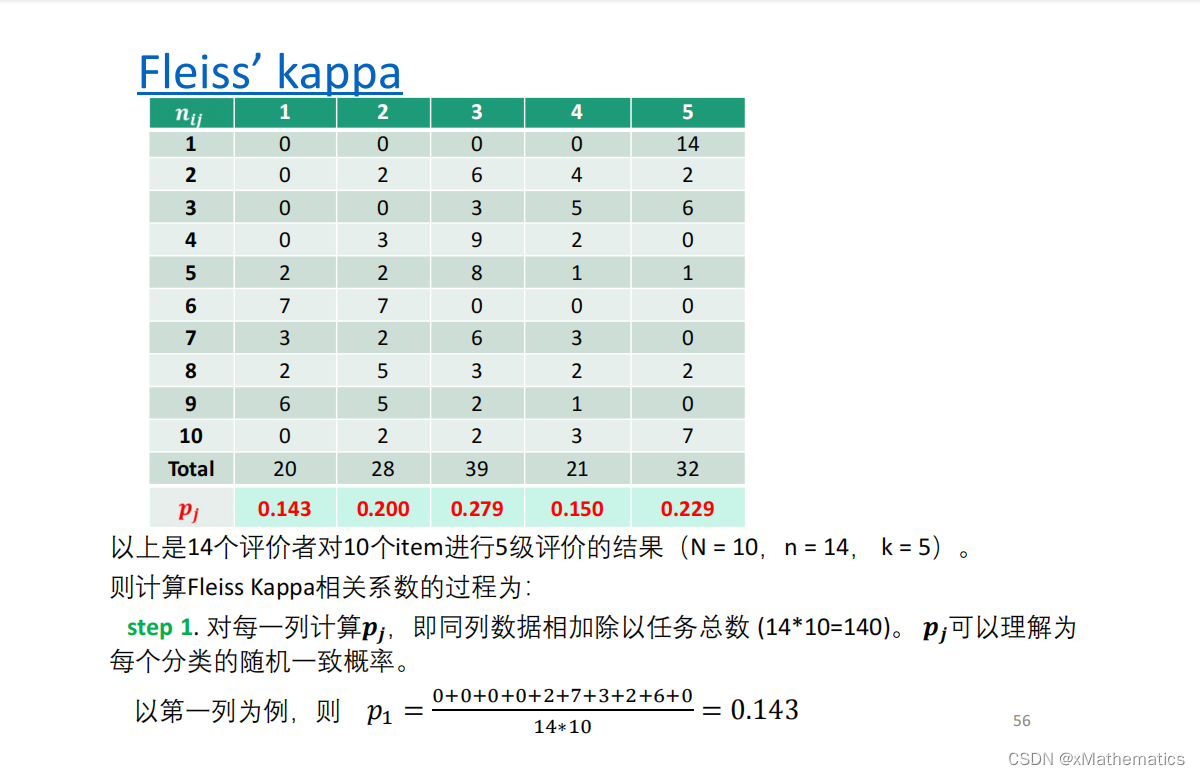
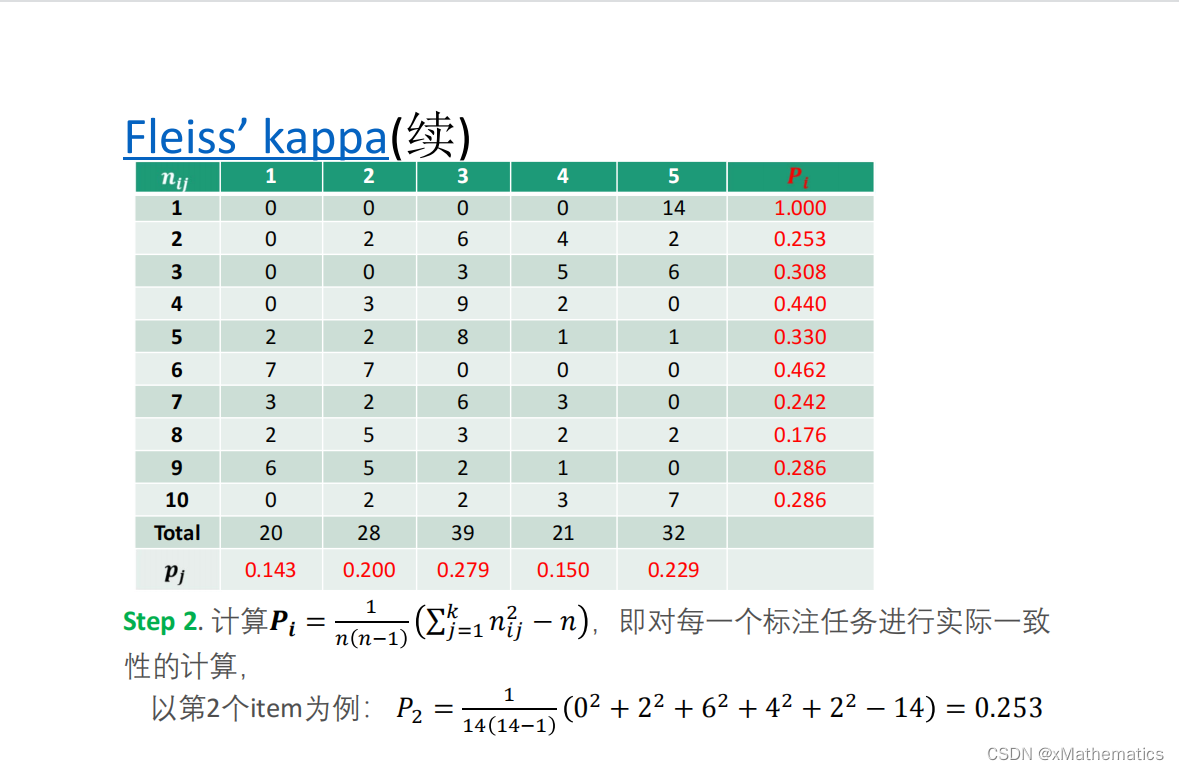
6、方法对比与选择建议

维度	皮尔森相关系数	Cohen’s Kappa
数据类型	连续变量	离散分类变量（名义/有序）
核心目标	线性相关强度	分类一致性（排除随机影响）
敏感因素	异常值、非线性关系	类别分布均衡性
典型场景	连续变量关联分析（如身高与体重）	医学诊断、分类模型评估

---

7、其他一致性评价方法

1. Fleiss’ Kappa：扩展至多个评价者的分类一致性分析。
2. AC1系数：解决Kappa悖论问题，尤其适用于高一致率但类别不平衡的场景。
3. 组内相关系数（ICC）：定量数据重复测量的一致性（如仪器信度检验）。
4. Bland-Altman图：可视化两种测量方法的一致性差异（如医学仪器对比）。

---

8、实践注意事项

1. 数据预处理：检查正态性（皮尔森）或类别平衡性（Kappa）。
2. 结果解读：结合统计显著性（p值）和效应量（如Kappa值）综合判断。
3. 方法互补：分类数据可同时报告Kappa和简单一致率；连续数据可联合使用皮尔森与散点图。

通过合理选择方法，可科学评估变量间关联或评价者间一致性，为科研、医疗及工业场景提供可靠依据。