1、结论
条件概率密度、条件期望、条件方差的表达式如下:
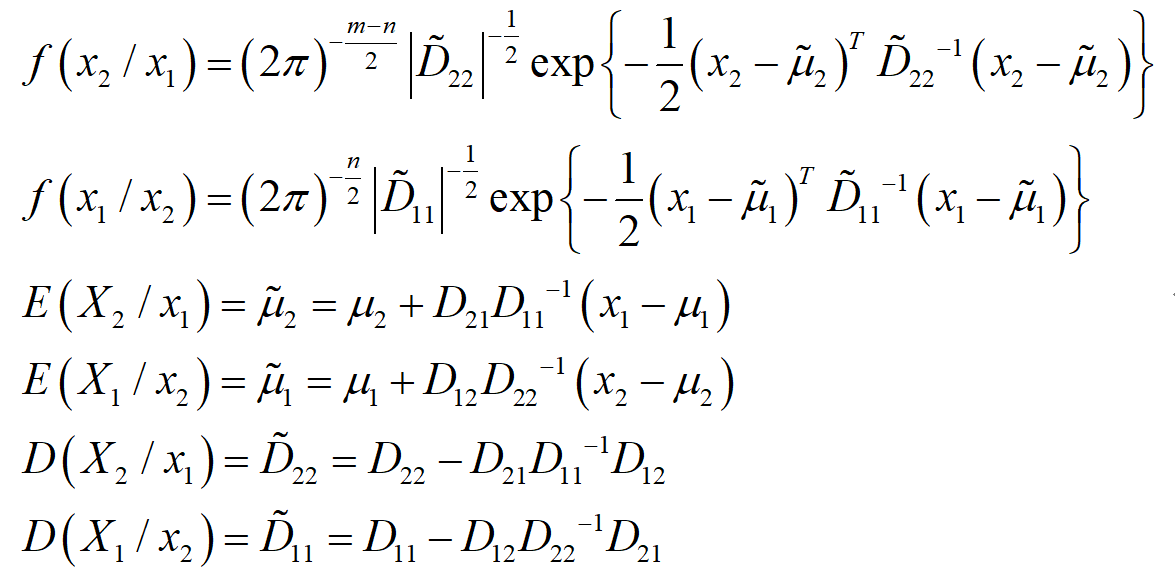
2、推导
可以把目的描述成下面的样子:

分块矩阵求逆及矩阵反演公式由来:https://blog.csdn.net/Gou_Hailong/article/details/121062002



条件概率密度、条件期望、条件方差的表达式如下:
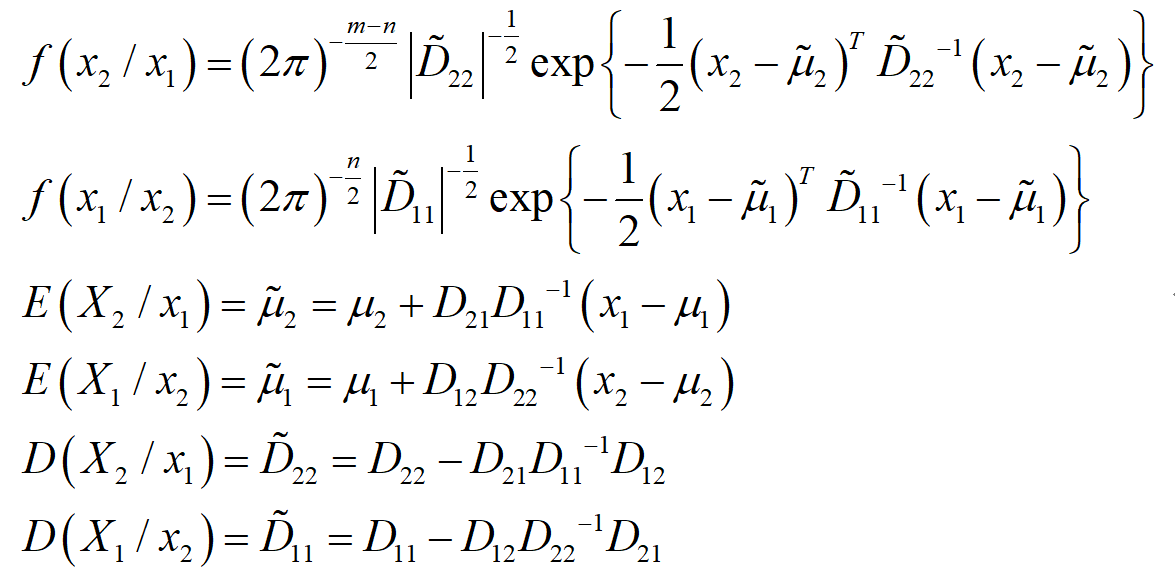
可以把目的描述成下面的样子:

分块矩阵求逆及矩阵反演公式由来:https://blog.csdn.net/Gou_Hailong/article/details/121062002



 8091
8091
 1266
1266
 5459
5459

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


