前言
本人专业电子信息工程,想走电源方向,用克里斯多夫·巴索所著《开关电源控制环路设计》(机械工业出版社翻译)入门,书的前四章为基础部分,已经读了两遍,这篇博客是第三遍,每次读都有收获,这次把读书过程给记录下来,留作整理和纪念
在阅读本书之前,本人已学习信号与系统、模电、电分前置课程,对 PID 控制算法也有一些认识,故这些部分本博客将不多赘述。之后将使用 Mathcad 等常见工程软件对书中部分计算式、电路等实例进行仿真。希望我的系列博客可以帮助像我一样的菜鸟摸到点电源的门槛,也欢迎各路大神批评指正
本系列博客将完全循原书的目录及线索对书中内容进行再现,因此阅读本博客时一定一定要先确保手里有原书的纸质或者电子档。且我也将使用童诗白、华成英编《模拟电子技术基础》、李瀚荪编《电路分析基础》等教材作为参考书,届时会尽可能地截图说明
第 1 章 环路控制基础
引言
此处以生物反馈环路为例引入反馈控制系统,而对于本书中常见的环路控制,则是以开关型稳压电路如 Boost 电路作为控制系统 H(s)。将基准电压 Vref 作为 H(s) 的输入,并通过扫频研究 H(s) 的电压增益、输出阻抗等频响特性,寻找合适的穿越频率及其匹配的以相位为首的各种裕度。循 PID 理念通过配置系统零极点来构造补偿器 G(s) ,两者将通过 PWM 比较电路级联。控制系统 H(s) 与补偿器 G(s) 将组成系统的开环增益 Tcl(s) = H(s)·G(s),输出电压 Vout 将通过电阻分压反馈回输入,构成闭环系统
对于上述闭环系统,其中一个图例位于本书 P107,图 3.60

此外,作为本书封面图 P118,图 4.10 将此关系描述得更加简洁
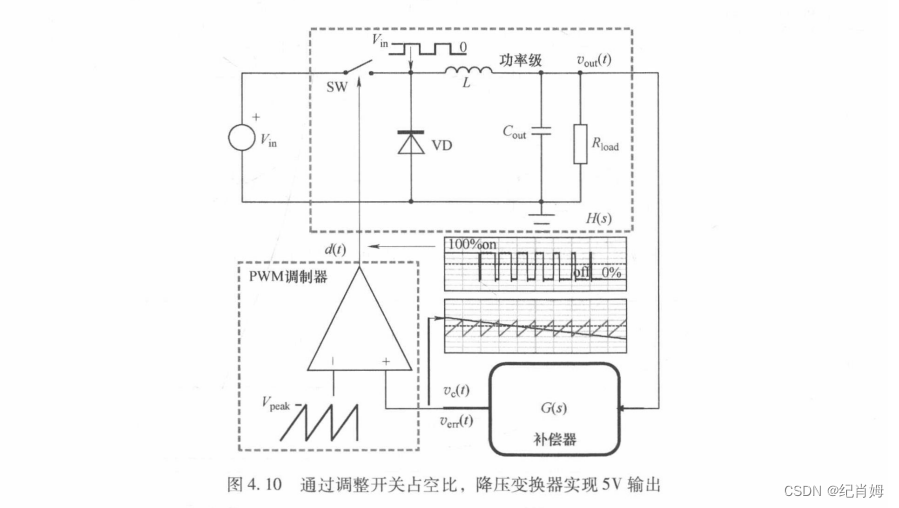
而在实际电路实现的时候,考虑到使用过程中的安全性,还会采用如光电耦合器等隔离元件实现电气隔离,前 4 章不做考虑
1.1 开环系统
此章节中值得注意的是对于前向通道的描述,即从输入 u 到输出 y 的各个模块的总和被称为前向通道,对应 P55,图 3.1 中的 H(s) 部分,而反馈通道对应图中 G(s) 部分,这似乎是在自动控制原理中常用的表述,本博客后文也将沿用这一表述。

但对于本书中的大部分情况而言, 闭环系统应当更接近于 P68,图 3.18 的情况,其中 G(s) 不再表示反馈网络,而表示与控制环节 H(s) 同处在前向通道中的补偿器环节 G(s),需要注意

1.1.1 扰动
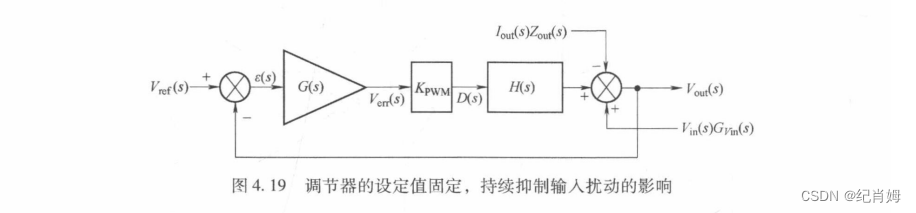
本书大部分语境下的扰动是指电源系统的输入电压改变以及输出负载阶跃,对于后者通常是用电流源负载的电流阶跃进行模拟。可用叠加定理个别分析,图例见 P126,图 4.19
1.2 控制的必要性——闭环系统

如文中所说,在设计闭环系统的时候反馈输出端相位及误差信号增益十分重要
文中所提及的误差信号和输出变量变化趋势相反的变化关系丢失的意思是,在电路中反馈回路回到输入的时候相位在 0 或 360° (考虑基于 OPA 的加法器反向输入带负号时为 180° )左右时,反馈和输入同相,误差信号将在反馈过程中反复地放大,此时系统将是发散的。
电路中相位的改变量来源于前向以及反馈回路,当反馈回路为导线 Fn(s) = 1 或为纯倍增(电阻分压或理想 OPA 放大)时,反馈回路不会产生相移。而前向电路传函中的零极点根据不同种类以及类别将在各个频段产生不同相移,此关系可见 P63 3.2.2 开篇对 LHP 零极点的叙述
当传递函数中出现纯延迟或右半平面极点或零点时,必须多加小心。因为直观来说,如果在伯德图中看到 +1 斜率的幅值变化,则零点正在起作用,此时相位会增加并在某个频率点达到 +90° 。同样的道理也适用于极点,-1 斜率的幅值变化,应该会使相位在某个频率点达到 -90° 。如果将极点和零点组合在一起,可以看到相位首先走向 -90°,然后在零点起作用后返回到 0 。在数学上,你可以写出最小相位系统具有的高频相位渐近线,定义为
φmax= - 90° (n-m) (3.10)
式中,n 是极点数量;m 是零点数量;例如:5个极点和 4 个零点给出 -90° 的相位渐近线。
必须注意,上述结论仅在最小相位系统中成立,最小相位系统即仅有左半平面(LHP)零点或极点的系统,一阶系统只有一个极点,相位偏移为 -90° ,二阶系统若只有两个极点,则为 -180°
RHP 零极点的相位表现与 LHP 者相反,幅值表现相同,且将使系统不稳定,也可用《信号》课程中的复频域收敛域概念理解
文中所提及的功率变换器,在本书中主要表现为 DC-DC 变换器,在这之中又以 Boost (并联开关型稳压电路)等电路为首。在参考书《模电基础》P468,9.6 开关型稳压电路 有对其详尽的介绍,本书后文 P41 2.5.1 一个两步转换过程,也首次提及(下图 9.6.1 来自参考书)


对于《模电基础》P468 中的换能电路的输入信号来自于 PWM 模块。即本书中 P89,图 3.37 首次提及的脉宽调制器,也被称为 XPWM 模块,是一种用比较器和斜坡信号发生器与输入误差比较输出 PWM 控制信号的方波发生器。

1.3 时间常数的概念
时间常数 τ,表示系统的响应时间,系统从某一个稳态到另一个稳态所需时间,在参考书《电路(上)》P239 6-4 章节 零输入响应 中对时间常数以及系统的固有频率给出解释,可知定性而言系统在 1 倍 τ 后稳态转换完成度为 63%,3 倍 τ 后稳态值误差小于 5%
对于 RC 或 RL 电路,时间常数的定义为 τ = RC 或 τ = L/R,此处 R 为电容或电感两端看出去的除源阻抗

本书中利用 RC 低通滤波这一经典例子给出时间常数定义,使用微分方程求解。我数学底子不好,对于求解此类电路,我更倾向于使用拉普拉斯变换方法,此时需要通过电路获取传递函数。获取传递函数的方法,通常是阻抗比分压法,而对于此类 “熵值较低” 的电路,也可以通过本书所给观察法求解,位于 P26 2.2.1 观察法找极点和零点
在此使用阻抗比分压方法,在 Mathcad 中绘制图形

如上图敲出传函计算式,利用工具栏 - 插入 - 图形 - X/Y 绘图可得出 RC 低通传函的阶跃响应。以 10 V 阶跃作为输入,可看到和书中相同的响应波形:均在 3e-4 时刻达到下一稳态的 95% 处,由于时间常数为 1e-4 ,此时刻即为 3τ ,输出波形符合 3τ 原则

阻抗比分压法,即用电容电感阻抗简单等效公式及电路分压关系来求得输入输出间的电流电压关系,从而得到系统传递函数,简单等效公式可见参考书《电路(下)》P29 向量模型的引入
什么是相量模型呢?以前所用的电路模型,以 R、L、C 等原参数来表征元件,称为时域模型,它反映了电压与电流时间函数之间的关系。也就是说,从该模型可列出电路的微分方程,从而解出未知的时间函数。相量模型则是一种运用相量能很方便地对正弦稳态电路进行分析、计算的假想模型。它和原正弦稳态电路具有相同的拓扑结构,但原电路中各个元件要用阻抗(或导纳)表示,也就是说,在作相量模型时,要把每个电容元件看作是具有,1/jwC 值的阻抗,把每个电感元件看作是具有 jwL 值的阻抗,把每个电阻元件看作是具有R值的阻抗。该模型中的电压、电流都是代表原电路图中各正弦电压、电流的相量,其参考方向仍与原电路相同。由于实际上并不存在用复数来计量的电压和电流,也没有一个元件的参数会是虚数,所以相量模型是一种假想的模型,是对正弦稳态电路进行分析的工具。
可将向量模型公式中的 jw 替换为 s,因为当线性系统稳定且初始值为 0 时,傅里叶变换和拉氏变换是等价的,他们可以给出相同的结果 P15 1.5.1 拉普拉斯变换
阻抗比分压法可以代替绝大多数的复杂微分方程计算,且可以获取电路网络的传递函数,此后若无特殊需求,本博客均使用此方法求解任何电路问题
顺带一提,使用电分中时域分析章节三要素法也可以求解低阶电路网络时域方程,如下为三要素法公式,位于参考书《电路(上)》P253
(1) 用电压为 uC ( 0 ) 的直流电压源置换电容或用电流为 iL ( 0 ) 的直流电流源置换电感,所得电路为一直流电阻电路,称为 t = 0 时的置换电路,由此电路可求得任一电压或电流的初始值,即 y ( 0+ ) 。
(2) 用开路置换电容或用短路置换电感,所得电路为一直流电阻电路,称为 t = ∞ 时的置换电路,由此电路可求得任一电压或电流的稳态值,即 y ( ∞ ) 。
(3) 求 Nt 的戴维南或诺顿等效电路以计算电路的时间常数 τ = R0*C 或 т = L/R
(4) 根据以上所得数据可绘出波形图,并直接写出所需结果。或根据所得
数据代入下列公式也可得出所需结果。

1.3.1 时间常数的应用
由于时间常数的延时,控制系统不能依靠简单的比例算法进行优良的输出,而是需要考虑系统的响应时间、振荡过冲等因素。在 P7 图1.9 中所提及的上升时间等参数可在 P80 表 3.1 进行快速查阅,或 P74 寻找信息参数定义与说明

此处波形仅告知了此为二阶控制系统典型响应,并未告知实际的电路以及各项参数,登入以下 TI 滤波器设计网站(需要登录),依次点击 Low-pass、左侧 Filter order 中选择 2 阶滤波器、点击右下对应 Butterworth 滤波的 select> 选项,可获取一个典型有源二阶低通滤波器。 Filter Design Tool (ti.com) https://webench.ti.com/filter-design-tool/filter-type 滤波器的电路网络示意图即各个元件的具体参数如下
https://webench.ti.com/filter-design-tool/filter-type 滤波器的电路网络示意图即各个元件的具体参数如下

网站直接给出此二阶电路的阶跃响应
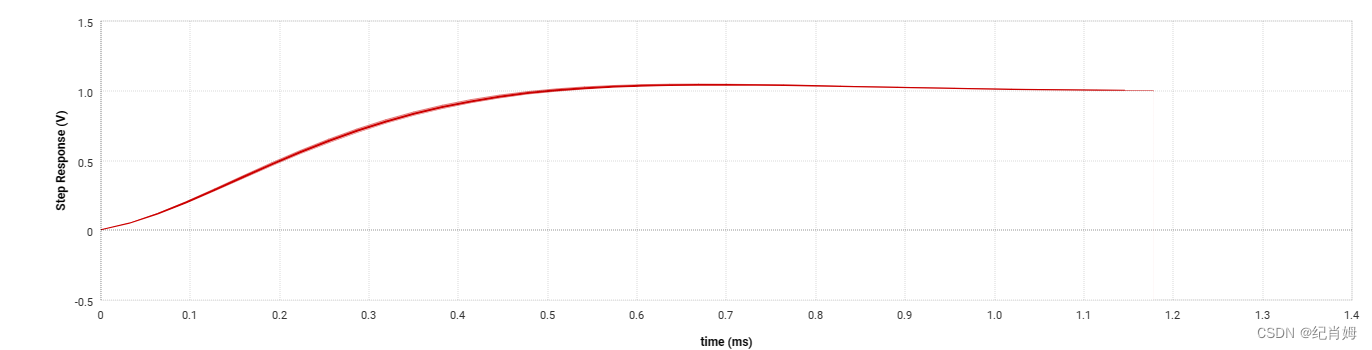
观察此图像,可看出其上升时间约为 0.35 ms,超调量约为 0.04 V
也可通过 multism 进行电路仿真,注意将信号源设置为方波或输入直流带开关,以便观察阶跃响应特性。或使用 Mathcad 及 Matlab 进行数值计算,更便于理论分析以及得到清晰的波形
电路解算方法:利用运放虚短虚断特性及基尔霍夫构建阻抗表示的电压传递函数,必要时设置中间电位辅助计算,在此不多赘述
PID 参数对系统的影响总结:
比例环节:又称增益,kp 越大,反应速度越快,超调量越大,静态误差越小。系统的增益直接关系到反馈量的大小,直接影响系统的控制精度
微分环节:kd 越大,反应速度越慢,超调量越小,同 kp 改善暂态响应
积分环节:ki 用于消除稳态误差(直流误差),改善稳态性能
1.3.2 比例环节
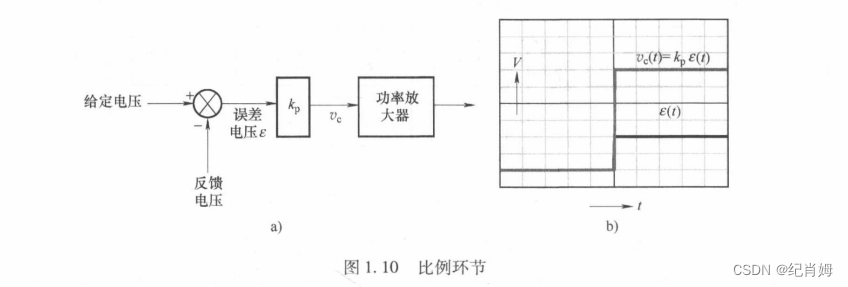
此环节为适用于任何频段的纯增益环节,理想状态下不带有相移特性。可通过电阻分压网络或使用 OPA 同相、反相放大电路来实现此环节,Multsim 中可采用此方式仿真
使用 Matlab 进行仿真,由于此后使用 Matlab 的频率相当高,我制作了一个研究传递函数的合集代码,实现输入传函表达式即可获取开环及闭环下的零极点图、伯德图、奈奎斯特图、阶跃与正弦响应波形,代码见下,注意其中代码尾部的图片保存路径需要自己设定
% /* USER CODE BEGIN SysInit */
close all; clc; clear; % 程序初始化
time = linspace(0, 200e-6, 5000); % 此处设置响应波形时间显示区间
Omega2Freq = false; % 在伯德图中横坐标使用频率代替角频率
Bode2Nyquist = false; % 使用奈奎斯特图代替伯德图
DisplayInputs = false; % 将输入信号一并绘制在响应波形图像中
gain_ol = 10; % 前向通道增益,单位分贝
gain_cl = 0; % 反馈通道增益,单位分贝
nums_tf = {1}; % 前向通道的传函分子
dens_tf = {1}; % 前向通道的传函分母
nums_fn = {1}; % 反馈通道的传函分子
dens_fn = {1}; % 反馈通道的传函分母
step_input = stepfun(time,0).*1; % 设置阶跃响应输入信号
step_start = 0; % 设置阶跃响应零时刻状态
sinu_input = sin(1000.*2.*pi.*time).*1; % 设置正弦响应输入信号
sinu_start = 0; % 设置正弦响应零时刻状态
% /* USER CODE END SysInit */
% /* USER CODE BEGIN */
% figures deploy 此处可改值以适配不同分辨率的显示器
figure_handle = {}; for cycle = 1:6 figure_handle{end+1} = figure; end
dleft = {10,580,1150,10,580,1150}; dbottom = {560,560,560,50,50,50};
for cycle = 1:6 movegui(figure_handle{cycle},[dleft{cycle} dbottom{cycle}]); end
% transfer functions
for cycle = 1:numel(nums_tf)-1 nums_tf{end} = conv(nums_tf{end},nums_tf{cycle}); end
for cycle = 1:numel(dens_tf)-1 dens_tf{end} = conv(dens_tf{end},dens_tf{cycle}); end
for cycle = 1:numel(nums_fn)-1 nums_fn{end} = conv(nums_fn{end},nums_fn{cycle}); end
for cycle = 1:numel(dens_fn)-1 dens_fn{end} = conv(dens_fn{end},dens_fn{cycle}); end
sys_ol = tf(nums_tf{end},dens_tf{end}); gain = db2mag(gain_ol); sys_ol = sys_ol.*gain;
sys_cl = feedback(sys_ol,tf(nums_fn{end},dens_fn{end})); gain = db2mag(gain_ol); sys_cl = sys_cl.*gain;
% waveform plot of openloop
options = bodeoptions; options.FreqUnits = 'Hz';
figure(figure_handle{1});
pzmap(sys_ol); grid on; title('Zerp-Ploe Map of Tol(s)');
figure(figure_handle{2});
if(Bode2Nyquist == false && Omega2Freq == true) bode(sys_ol,options); grid on; title('Bode Diagram of Tol(s)'); end
if(Bode2Nyquist == false && Omega2Freq == false) margin(sys_ol); grid on; title('Bode Diagram of Tol(s)'); end
if(Bode2Nyquist == true) nyquist(sys_ol); grid on; title('Nyquist Diagram of Tol(s)'); end
figure(figure_handle{3});
subplot(2,1,1); step_response = lsim(sys_ol,step_input,time,step_start); plot(time, step_response); xlim([min(time) max(time)]);
title('Step Response of Tol(t)'); xlabel('time (s)'); ylabel('amplitude'); grid on;
if(DisplayInputs == true) hold on; plot(time, step_input); end
subplot(2,1,2); sin_response = lsim(sys_ol,sinu_input,time,sinu_start); plot(time, sin_response); xlim([min(time) max(time)]);
title('Sinusoidal Response of Tol(t)'); xlabel('time (s)'); ylabel('amplitude'); grid on;
if(DisplayInputs == true) hold on; plot(time, sinu_input); end
% waveform plot of closeloop
figure(figure_handle{4});
pzmap(sys_cl); grid on; title('Zerp-Ploe Map of Tcl(s)');
figure(figure_handle{5});
if(Bode2Nyquist == false && Omega2Freq == true) bode(sys_cl,options); grid on; title('Bode Diagram of Tcl(s)'); end
if(Bode2Nyquist == false && Omega2Freq == false) margin(sys_cl); grid on; title('Bode Diagram of Tcl(s)'); end
if(Bode2Nyquist == true) nyquist(sys_cl); grid on; title('Nyquist Diagram of Tcl(s)'); end
figure(figure_handle{6});
subplot(2,1,1); step_response = lsim(sys_cl,step_input,time,step_start); plot(time, step_response); xlim([min(time) max(time)]);
title('Step Response of Tcl(t)'); xlabel('time (s)'); ylabel('amplitude'); grid on;
if(DisplayInputs == true) hold on; plot(time, step_input); end
subplot(2,1,2); sin_response = lsim(sys_cl,sinu_input,time,sinu_start); plot(time, sin_response); xlim([min(time) max(time)]);
title('Sinusoidal Response of Tcl(t)'); xlabel('time (s)'); ylabel('amplitude'); grid on;
if(DisplayInputs == true) hold on; plot(time, sinu_input); end
% informations
[nums_tf{end},dens_tf{end}] = tfdata(sys_ol,'v'); [zero,pole,gain] = tf2zp(nums_tf{end},dens_tf{end}); fprintf('OpenLoop Info:');
fprintf('\nGain:'); fprintf(' %g', gain); fprintf('\nZero:'); fprintf(' %g', zero); fprintf('\nPole:'); fprintf(' %g', pole);
[gm,pm,wcg,wcp] = margin(sys_ol); fprintf('\nGm:%.2f dB Pm:%d deg Wcg:%g Hz Wcp:%g Hz\n\n',gm,pm,wcg/2/pi,wcp/2/pi);
[nums_tf{end},dens_tf{end}] = tfdata(sys_cl,'v'); [zero,pole,gain] = tf2zp(nums_tf{end},dens_tf{end}); fprintf('CloseLoop Info:');
fprintf('\nGain:'); fprintf(' %g', gain); fprintf('\nZero:'); fprintf(' %g', zero); fprintf('\nPole:'); fprintf(' %g', pole);
[gm,pm,wcg,wcp] = margin(sys_cl); fprintf('\nGm:%.2f dB Pm:%d deg Wcg:%g Hz Wcp:%g Hz\n',gm,pm,wcg/2/pi,wcp/2/pi);
% picture saving 此处需要修改保存路径
saveas(figure_handle{1}, 'E:\SMPS\Simulated waveform diagram\Buff\pzmap_ol.png');
saveas(figure_handle{3}, 'E:\SMPS\Simulated waveform diagram\Buff\response_ol.png');
saveas(figure_handle{4}, 'E:\SMPS\Simulated waveform diagram\Buff\pzmap_cl.png');
saveas(figure_handle{6}, 'E:\SMPS\Simulated waveform diagram\Buff\response_cl.png');
if(Bode2Nyquist == true) saveas(figure_handle{2}, 'E:\SMPS\Simulated waveform diagram\Buff\nyquist_ol.png'); end
if(Bode2Nyquist == true) saveas(figure_handle{5}, 'E:\SMPS\Simulated waveform diagram\Buff\nyquist_cl.png'); end
if(Bode2Nyquist == false) saveas(figure_handle{2}, 'E:\SMPS\Simulated waveform diagram\Buff\bode_ol.png'); end
if(Bode2Nyquist == false) saveas(figure_handle{5}, 'E:\SMPS\Simulated waveform diagram\Buff\bode_cl.png'); end
% /* USER CODE END */
此处验证比例环节,仅需要调整开环增益,参数调整如下:
% /* USER CODE BEGIN SysInit */
close all; clc; clear;
time = linspace(0, 200e-6, 5000);
Omega2Freq = false;
Bode2Nyquist = false;
DisplayInputs = true;
gain_ol = 4;
gain_cl = 0;
nums_tf = {1};
dens_tf = {1};
nums_fn = {1};
dens_fn = {1};
step_input = stepfun(time,20e-6).*1;
step_start = 0;
sinu_input = sin(1000.*2.*pi.*time).*1;
sinu_start = 0;
% /* USER CODE END SysInit */运行代码即可获取开环阶跃信号响应
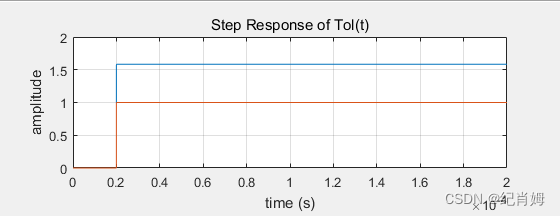
1.3.3 微分环节

微分环节的时域阶跃响应分析可转至频域通过拉普拉斯变换解得。在时域中微分相当于频域中 s 相乘,此性质在后文也有提及,在前向通道传函中分子项改为 [1,0] ,代表以 s 为变量的多项式,一次项系数为 1 ,常数项为 0 。即分子式:s 。又因为在 matlab 中,无论是 lsim 或是 step 函数,均不接受分子阶数大于分母阶数的传函,则通过设置超高频极点,以将分母拉到一阶的情况下,尽可能地减少此极点对微分环节的影响,经过多次测试,发现极点设置于 1e5 处最佳,那么分母多项式应该改为 [1e-5,1] 。又由于改变分母会不可避免地导致增益变大,为了直观看出输入输出关系,则根据 dB 作为单位时的每十倍频改变 20dB 原则,将前向增益改为 -20.*5 ,为了复制书中输入输出间的两倍关系,再为增益加上 6dB ,最终参数的改动如下:
% /* USER CODE BEGIN SysInit */
close all; clc; clear;
time = linspace(0, 200e-6, 5000);
Omega2Freq = false;
Bode2Nyquist = false;
DisplayInputs = true;
gain_ol = -20.*5+6;
gain_cl = 0;
nums_tf = {[1,0]};
dens_tf = {[1e-5,1]};
nums_fn = {1};
dens_fn = {1};
step_input = stepfun(time,20e-6).*1;
step_start = 0;
sinu_input = sin(1000.*2.*pi.*time).*1;
sinu_start = 0;
% /* USER CODE END SysInit */此时得到波形:

顺带一提,在 multisim 中也可通过构造运放微分器并仿真来得到此波形
1.3.4 积分环节

积分环节阶跃同样可使用拉氏变换求解,时域积分一次相当于频域除以一次 s ,分子为 1 分母为 s 。若不拉高前向增益,需要延长时间才能清楚地看到积分效果。设定参数如下:
% /* USER CODE BEGIN SysInit */
close all; clc; clear;
time = linspace(0, 3, 5000);
Omega2Freq = false;
Bode2Nyquist = false;
DisplayInputs = true;
gain_ol = 0;
gain_cl = 0;
nums_tf = {1};
dens_tf = {[1,0]};
nums_fn = {1};
dens_fn = {1};
step_input = stepfun(time,1).*1;
step_start = 0;
sinu_input = sin(1000.*2.*pi.*time).*1;
sinu_start = 0;
% /* USER CODE END SysInit */最终仿真波形如下:
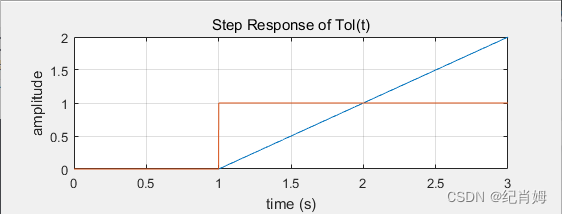
1.3.5 比例 - 积分 - 微分环节
在电路网络中将上述三个环节并联,传递函数将在 s 域相加,基由此可构造 PID 控制电路。此电路可由多种方式构造,可使用基于 OPA 的积分、微分、比例、反向等运算电路组成,也通过配置零极点的方式来达到与 PID 控制相同的效果。
经过本书后面对于输出阻抗的推导,可以证实上述方式的后者所构造的电路性能更加完好,而沿用经典 PID 理论所构造的电路输出会出现不可消除的振荡,完全无法工作。正如作者在 P162 中所言,开关电源的环路控制中的要点是通过配置零极点以获取预期的响应,而非经典 PID 理论
作者在大学期间学习的PID比较复杂,与作者现在更熟悉的零/极点放置没有直接联系。在本章中,经过一些代数运算可以发现,滤波PID实际上就是3型补偿器,它在功率变换器中被广泛使用。如果仅仅根据参考电压到输出的传递函数对开关变换器进行补偿,实际上对于整个系统来说是不完整的。大多数变换器实际上都工作在稳压模式,也就是当变换器经历投切载时,设定值(参考电压)是固定不变的。因此输出阻抗对暂态响应至关重要,它决定了系统的输出特性,反映设计的控制器能否得到没有振荡的响应。随后,将传统PID的设计方法用于电压模式Buck变换器时,结果显示系统出现振荡:而如果通过经典的零/极点配置技术来获得无谐振峰的输出阻抗,那么最终得到了阻尼良好的阶跃响应。这两种方法都把关注点集中在设定点到输出的传递函数稳定上,而没有特别注意输出阻抗。在第三个例子中观察输出阻抗的表达式,通过补偿器使输出阻抗呈现完全阻性,在负载突变时,使得到的输出结果呈现为方波信号,没有超调现象。这种技术广泛用于个人计算机中主板供电的高速DC-DC变换器,以及其他对负载阶跃响应要求严格的应用场合。
1.4 反馈控制系统的性能

此图用于帮助读者理解暂态和稳态过程,来自于变换器的阶跃响应,同样未给具体电路以及参数。对于开关变换器,本书中于 P41 2.5.1 一个两步转换过程 首次提及两开关 Boost 变换器,使用 Multisim 对其进行仿真

本书的 P43 给出了假设的运行参数

在 multisim 中绘制

其中 S1 型号为 Basic - switch - TD_SW1 ,设定接通时间为 5.83*10^-6 、设定关断时间为 4.17*10^-6 。最终通过控制开关 S2 获得如下波形

可看出此波形振荡严重,与书中所示完全不符,推测是书中所指代变换器为接受过补偿后的闭环系统,而非单独的控制输出变换器。同时,输出到达稳态时幅值仍为 10 V,并非文中 24 V ,可能是电容参数设置有误
此处仿真未能完成,标题标红处理,之后再来填坑
1.4.2 阶跃信号
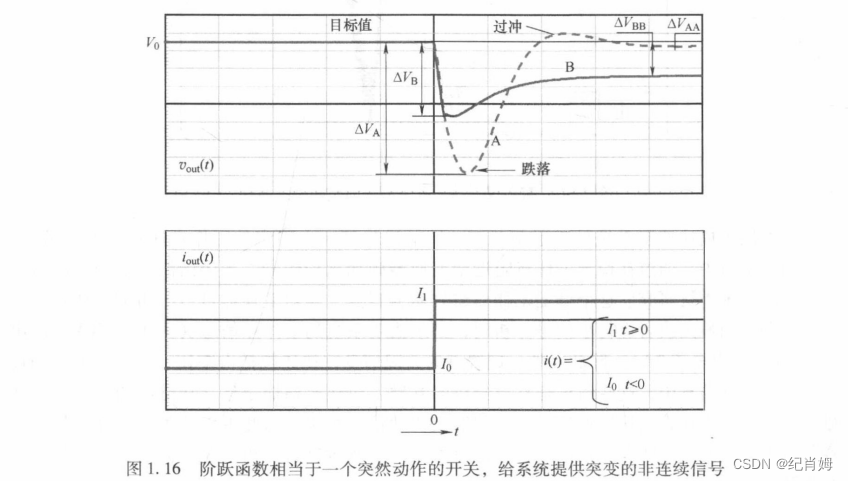
同上属变换器,与二阶系统区别的是,此处变换器接收的是来自负载阶跃(输出电流)阶跃的扰动,而非设定值的改变,故可看到图像中 A 、B 响应均是趋向目标值,输出电流的影响则是次要的。而且由于是变换器,同上标题标红处理
1.4.3 正弦信号
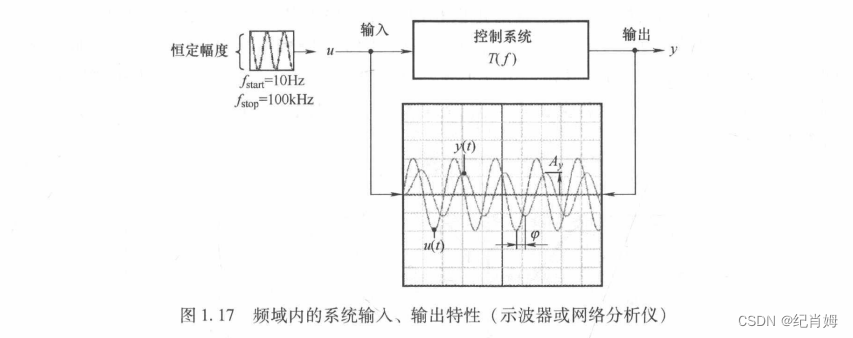
图中 u(t) 经过系统后幅值下降并存在延时,很多系统特别是无源电路网络均有此种特性,以本书的第一张波形图 RC 低通滤波阶跃为例,在 matlab 中求其正弦响应,可观察到如下波形

其中,蓝色线为输出信号
另外,此处扫频方法被应用于获取系统伯德图,利用伯德图可提取稳定(最小相位)系统的零极点。另外在本书 P259,图 5.79 有通过幅值变化情况确定极点的实例

1.4.4 伯德图

伯德图中的纵横轴均采用对数坐标,且纵坐标循下列公式,使用 Mathcad 以快速获取特殊分贝值和倍数的替换关系

此外,对于功率,每 10 倍频 10dB,对于电压,每 10 倍频 20dB
绘制伯德图需要计算柴楠的幅值与相移,公式 P18,1.30 、1.31
依旧以 RC 低通为例,观察其伯德图

在最小相位系统中,即传函仅有左半平面零点(LHPZ)与左半平面极点(LHPP)时,伯德图中的幅度谱和相位谱是相互关联的,也就是说,两个频谱图是可相互重现的,P63 有详细介绍
数学上,HendrikBode证明了当传递函数的极点和零点都位于左半平面时,传递函数频率特性的虚部和实部是相互关联的,对应的,其幅值与相位也是相互关联的。也就是,能够从幅值图重建相位图,反之亦然,如图3.11a曲线所示,传递函数满足这种情况的系统称为“最小相位系统”。但如果传递函数中出现右半平面零点或右半平面极点,则它们会像图 3.11b 所示的那样扭曲相位信息,这违背了伯德定律,这样的系统称为“非最小相位系统”。此外,当传递函数中包括纯延迟环节时也会出现类似的情况,延迟不会改变传递函数的幅值,但随着频率的增加其相位滞后增加,从而改变相位响应,违背了伯德定律。在许多理论书籍中,明确指出在非最小相位系统中应谨慎使用伯德图,而应当改用奈奎斯特图。奈奎斯特图不会将实部和虚部组合起来用幅值和相位来表示,而是将实部和虚部单独绘制在平面上。因此,即使存在右半平面零点或极点(也称为不稳定极点或零点),它也可以分析和预测系统的稳定性,而不会产生歧义。

在最小相位系统中,相互重现的规则是,每一个极点处渐近线获得 -1 斜率,此时其带来的高频相位偏移正好达到 -45° 位置,零点则完全相反,其所在处有 +1 斜率变化以及 +45° 偏移。相位渐近线在 0 频率处为 0 ,在无穷频率时的相位值可由本博客 1.2 章节 处公式计算得到。绘制 0° 先到转折频率(首个极点)1/5 处,绘制高频相位线在转折频率 5 倍处。多个零极点的系统的伯德图曲线等于单个零极点曲线之和
1.5 传递函数
传递函数只和系统本身相关,与输入信号无关。传函的分母也被称为特征方程
1.5.1 拉普拉斯变换
时域上积分相当于频域上除以 s

微分则是乘 s

在本书 P91 3.138 中可得到时域延时性质

1.5.2 激励与响应信号
传函可被分为分子和分母,其根为零点与极点。另一种分类是通过输入和输出分类,输出除以输入也可得到传递函数。电路中并联传函将相加,串联(级联)为相乘。传函通过物理意义分类可分为如下六种
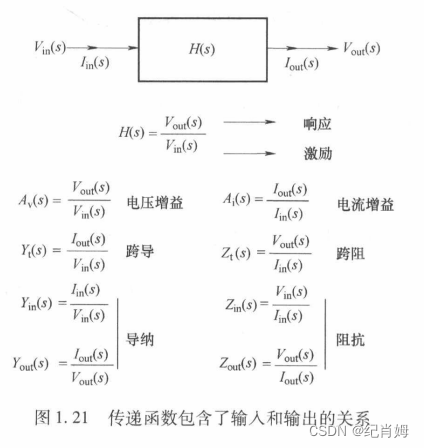
其中,电压增益以及输出阻抗是本书重点研究的对象,此两项传函直接影响变换器的输出
1.5.3 一个简单的范例
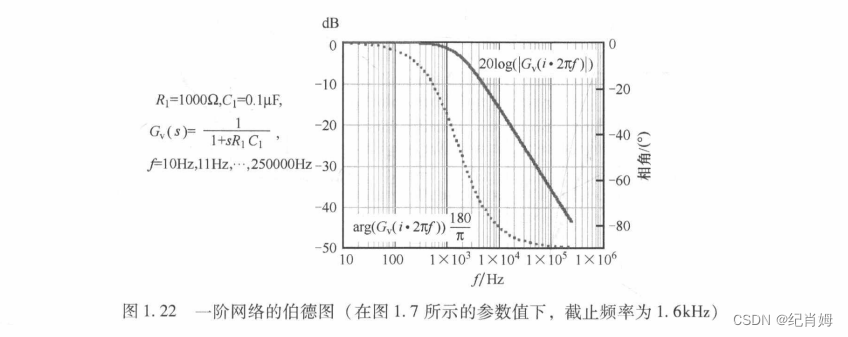
此处范例为讨论时间常数时所用低通电路,之前已在 Mathcad 中使用阻抗比分压求解过其传函,将值直接输入 matlab,可求得其伯德图,图形可见本博客 1.4.4 章节
1.5.4 组合传递函数的伯德图
伯德图有个十分重要的特性,即级联系统的子系统伯德图逐个频率点幅频相频值直接相加,可以得到整个系统的伯德图。这是得益于伯德图纵横轴的对数特性,级联系统的相乘传函形式在图像上变为了相加

观察频谱图,可知 H(s) 于 f1 处存在两个重合极点,零增益;G(s) 在 f2 处存在一个零点,且拥有 -10dB 增益;f2 > f1 约为3倍关系。而中间图 T(s) = H(s)G(s) ,为上方两幅图直接相加。
在 matlab 中复刻图像,值得注意的是,由于此处无需绘制响应曲线,则 G(s) 中无需添加高频极点处理。设 f1 = 101 rad/s;f2 = 303 rad/s,可得到如下关系
H(s): N(s) = {1};D(s) = {[1,100],[1,100]}
G(s): N(s) = {[1,300]}; D(s) = {1}
T(s): N(s) = {1,[1,300]};D(s) = {[1,100],[1,100],1}
其中,N(s) 、D(s) 为以 tf 函数输入参数形式表示的有关 s 的多项式,又因为传函本身也存在增益,可计算得到三个传函所需增益为:80、- 49.532 - 10、30.468 - 10
H(s) 的伯德图

G(s) 的伯德图
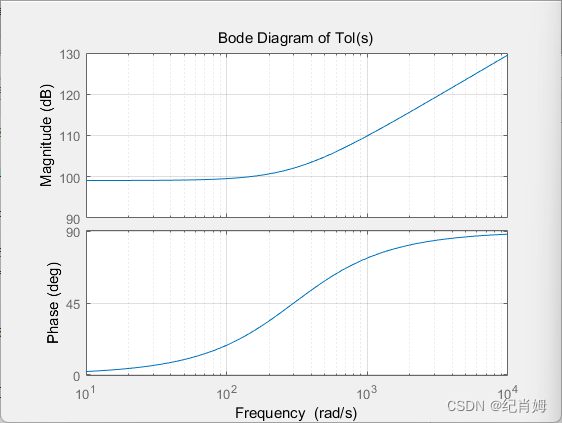
T(s) 的伯德图

需要注意的是,由于是使用内置函数 bode 或者 margin 函数绘制的图形,参数设置是由程序决定,故在阅读图像时一定要认清纵横轴坐标,若想更加直观地验证相加曲线,最简单的方式是根据上面的仿真图像纸笔绘制渐近线图像,再与最终结果进行对比
1.6 总结
本章对控制系统及相关术语进行了简要的介绍。在接下来的章节中,将分别就关心的主题进行详细介绍。当然,控制系统涉及的知识点非常多,需要付出足够的努力才能掌握。但是,如果需要关注的是较为简单的到中等复杂程度的线性或电力电子变换器,上述的介绍应该足够大家对这一领域有基本的了解。
后记
如作者总结,此章仅仅是对本书的简要概括与内容引入,而本书前 4 章要求读者阅读本书前所掌握技能部分罗列如下:
1,电分基础:基尔霍夫定理、带运放电路、戴维南诺顿定理、叠加方法、电容电感及耦合电感元件、一阶二阶电路、向量模型计算阻抗等
2,模电基础:电路输入输出阻抗计算、用 OPA 制作信号发生器、跟随器、运算电路、滤波电路、开关型稳压电路等
3,信号系统基础:傅里叶及拉普拉斯变换、通过电路网络求传函、常见激励、系统串并联、零极点图与稳定性联系等
4,自控基础:经典 PID 理论
5,仿真软件基础,我使用的是 Mathcad 、Matlab 及 Multisim,掌握程度也只是勉强够用
以上大部分基础知识在本书中都会进行详细解释,但并不系统,还是建议先学习前置课程掌握基础后再阅读此书
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








