感受野以及与卷积核运算比较——低调学习CNN(2)

感受野(Receptive Field)定义：

卷积神经网络各输出特征图中的每个像素点，在原始输入图片上映射区域的大小

---

我们来看一例子：
原始图片为5*5:

使用3*3的卷积核对其进行卷积操作，得到右下角特征图:

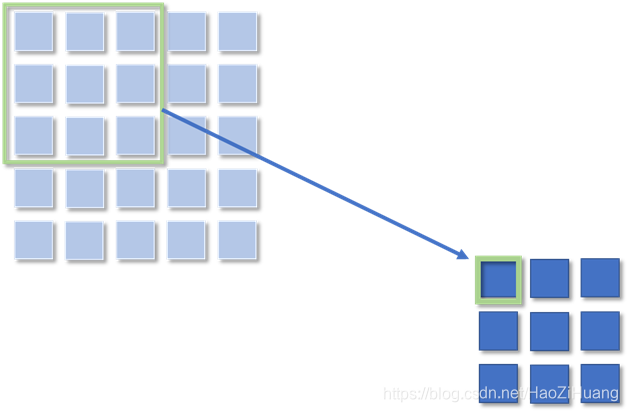
则右下角被绿色框框 框起来的像素点感受野为3

在对输出的3*3特征图进行3*3的卷积操作，得到1*1的特征图：

而该1*1的特征图的唯一像素点的感受范围为初始特征图，即其感受野为5

而我们也可以直接用5*5的卷积核对原图进行卷积操作:

则也同样得到1*1的特征图，该像素的感受野也是5

很明显，二者的特征提取能力是一样的。那么问题来了，我们是使用两个3*3的卷积核进行特征提取呢，还是直接使用5*5的卷积核进行特征提取呢？

如果你见过VGG等网络的结构，你可能会猜测，会选择两个3*3的卷积核进行操作，但究竟是为什么呢？

这个时候，我们就需要考虑，两种卷积运算所能承载的待训练参数和计算量

这里我们做假设，输入特征图的宽高均为$x$，卷积计算的步长为1
两层3*3的卷积核:

参数量：$3\times 3\times 2=18$
计算量：$(x-3+1{)}^2\times 9+(x-2-3+1{)}^2\times 9=18x^2-108x+180$

参数量：$5\times 5=25$
计算量：$(x-5+1{)}^2\times 25=25x^2-200x+400$

---

经简单运算得到$x>10$时，使用两层3*3卷积运算优于一次5*5的卷积运算

所以我们可以看到，在VGG网络中，只有3*3的卷积运算