电机控制理论学习---永磁同步电机控制策略

前言

本部分内容是对于永磁同步电机控制策略相关内容的学习，旨在记录自己的学习过程以及对知识点的一些理解，参考的文章会附上链接。若有理解不到位的地方，希望各位大佬批评指正。

本部分内容参考文章有：
如何快速理解永磁同步电机？
永磁同步电机中的磁阻转矩
弱磁控制｜MTPA控制｜永磁同步电机的转速从零增加到极限会发生什么？

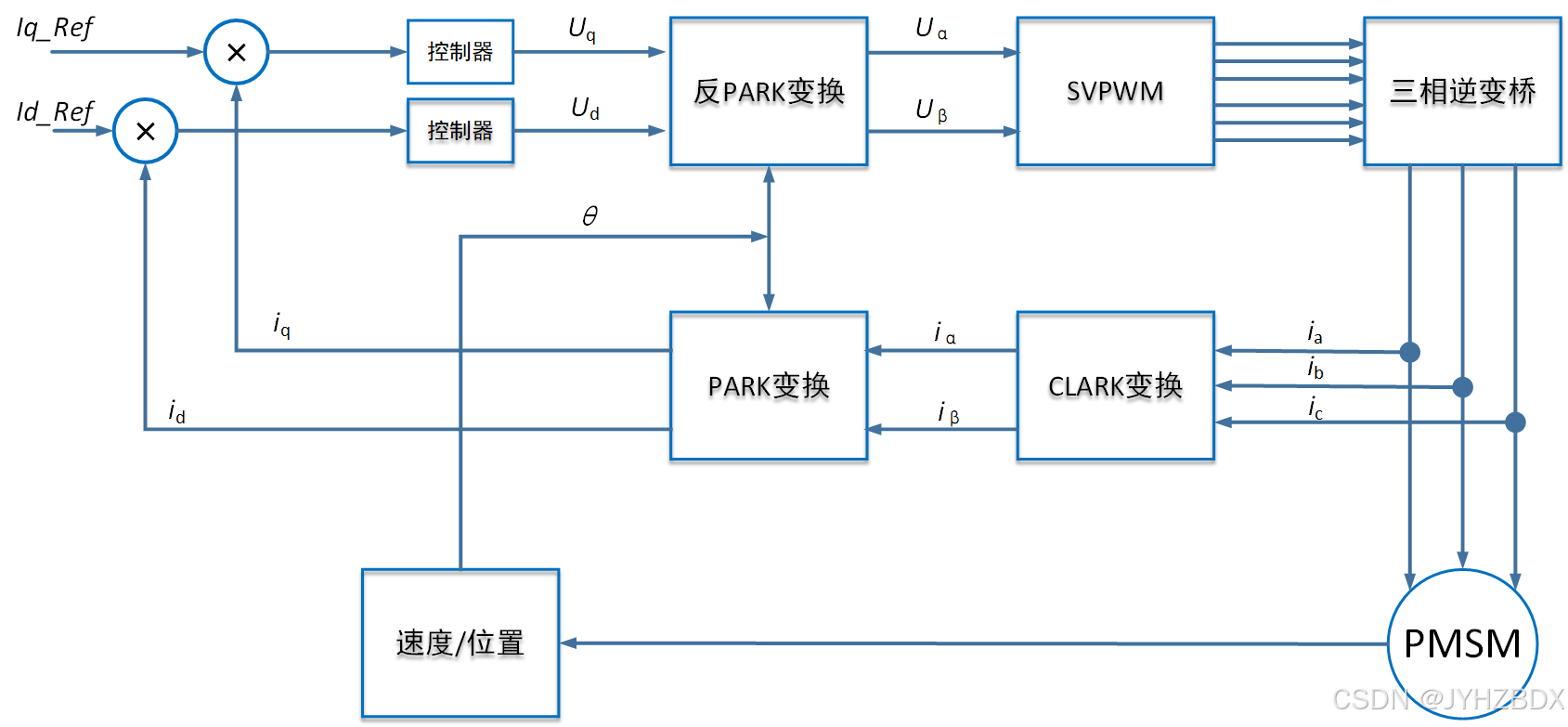
一、永磁同步电机矢量控制框图

现在要放上FOC必备框图了，其实这张图应该出现在学习过程中最初的地方，因为我们后边所有的学习内容都将围绕这张图进行。透过这个图，我们发现，后边再怎么花里胡哨，又是坐标变换，又是电压调制的，但这都是实现过程，问题是，当我想要获得一个固定输出力矩或转速时，我应该怎样给系统怎样的输入，当然，了解了电机四大方程之后，我们可能知道了系统的输入量或者被控制量就是电流，问题又来了，电流应该怎么施加给系统、电流给多大即能降低功耗又能获得响应的转矩或速度，这就需要熟悉一下控制策略。这篇文章先大概理一下基础理论，后续会补仿真，毕竟要仿真还得学控制器部分的内容。

图1. 永磁同步电机矢量控制

二、id=0

矢量控制中常用的，也是较为简单的一种控制方式是直接使$i_d=0$，理解起来也比较容易，因为在dq坐标系中，d轴指向转子方向，q轴垂直于转子方向，当d轴电流为0时，电流全部施加于q轴，此时，全部磁链均由转子永磁体产生，所有的电流都用来对转子永磁体产生力矩：$$T=\frac{3}{2}{p}_n{\psi }_f{i}_q$$

三、id≠0

1、转矩的组成

在此之前我一直认为d轴电流是没有用的，就像$i_d=0$控制策略中一样，只要让全部电流到q轴去，不就获得最大转矩了吗，事实不然，正如$i_d=0$控制策略中阐述的，它所产生的力矩也就是$$T=\frac{3}{2}{p}_n{\psi }_f{i}_q$$但前边也推导过，力矩的公式是这样的:$$T=\frac{3}{2}{p}_n({\psi }_f{i}_q+(L_d-L_q)i_d{i}_q)$$单从数学计算公式来看，似乎$i_d=0$并不会产生最大力矩，很显然，$i_d=0$把转矩公式中后边那部分内容丢掉了，我们把$i_d$、$i_q$表示为三角函数的形式，假设合成电流$i_s$与q轴夹角为$\theta$，那么有：$$i_d=-i_{s}sin\theta$$$$i_q=i_{s}cos\theta$$把转矩公式推导为夹角$\theta$的函数：$$T=\frac{3}{2}{p}_n({\psi }_f{i}_{s}cos\theta -(L_d-L_q)i_{s}sin\theta i_{s}cos\theta )$$$$T=\frac{3}{2}{p}_n({\psi }_f{i}_{s}cos\theta -\frac{i_s^2}{2}(L_d-L_q)sin(2\theta ))$$把转矩与夹角的函数关系通过图形表示出来，如图1所示，我们把图中蓝色曲线叫做励磁转矩，对应公式中左边这部分内容，图中红色曲线为磁阻转矩，对应公式中右半部分，总转矩就是两部分的和。通过图1也能明显看到，最大转矩并不在$i_d=0$处，而是要在总电流与q轴电流之间保持一定的角度才能发挥最大转矩。而该角度的取值可以通过对力矩公式求导取零得到，直接抄一下公式吧：$${\theta }_{maxT}=si{n}^{-}1(\frac{-{\psi }_m\pm \sqrt{{\psi }_m^2+8\ast i_s^2(\Delta L{)}^2}}{-4\Delta L{i}_s})$$这里的$i_s$表示的是总电流幅值，$\Delta L=L_d-L_q$
也可以根据图形法计算$i_d$、$i_q$电流如何分配时能够得到最大转矩，后边介绍。

图1.转矩的组成

2、磁阻转矩

在大神文章 永磁同步电机中的磁阻转矩中对磁阻转矩有生动形象的解释，根据这篇文章，把自己的理解记录下来。
磁阻转矩是去除永磁体的影响后，绕组对铁芯的力矩，如图2所示（有点丑，想画出 永磁同步电机中的磁阻转矩中图片的精髓，奈何水平有限，不过应该也能表达清楚），绿色部分为绕组，灰色部分为铁芯，白色部分为原本应该放永磁体的，但现在要单独研究磁阻转矩，就假想地把它抠出来，这样的话，转子上没有永磁铁，只有铁芯。当$i_d=0$时，磁感线示意图如图1所示，红蓝色磁感线分别为相邻的两个磁回路，即相邻的两个磁极产生的磁回路，当然这块已经不存在磁极了，因为永磁体被扣了，但不妨碍理解。可以看出来，q轴通入电流产生磁动势，因此，磁感线都从q轴通过，对于凸极式电机，q轴磁阻小于d轴磁阻（可以参考 电机控制理论学习—三相静止坐标系下电机方程中对于绕组电感的描述），所以磁感线是从转子中磁阻最小的地方走过，此时，绕组不会对转子产生转矩。

图2. id=0时磁场分布示意图 而当d轴通入电流时，如图3所示。d轴电流产生磁动势，强迫一部分磁感线从磁阻较大的d轴磁路通过，但磁感线会尽可能地找到磁阻小的磁路走，比如图中d轴绕组处两根磁感线，其中一根按照磁动势的指引通过转子中较细的d轴区域，这个磁感线的走向导致本就磁阻大的转子d轴更加雪上加霜，于是另外一根磁感线另辟新径，通过宽大的转子铁芯区域流向未有磁感线通过的d轴区域，从d轴流出的两根磁感线会向q轴靠近，因为q轴也有电流，也会产生磁动势，就这样磁感线歪七扭八的完成闭合，直观上也能看出来，此时并非稳定状态，因为磁感线并没有在转子上磁阻最低的磁路走过，本身携带有一定的能量，这部分能量会迫使磁感线按照最低磁阻磁路走，从而产生转矩。这就是磁阻转矩的定性理解。

图3. id≠0时磁场分布示意图

3、MTPA控制

MTPA，最大转矩电流比控制，它的控制目标是利用最小的电流输出最大的转矩，其实在图1中已经有初步的介绍，就是通过选取合适的$\theta$角，保证在输入相同总电流的情况下输出最大转矩，这一部分内容我们利用图解法求出输出不同转矩时需要的总电流以及d、q轴电流。
在转矩已知条件下求解电流，因此，首先把转矩公式做个变形：$$i_q=\frac{T}{1.5p_n({\psi }_f+(L_d-L_q)i_d)}$$可以看到，在转矩固定时，q轴电流与d轴电流成反比，分别取几个转矩，可以得到$i_d$、$i_q$的等转矩曲线簇，如图4所示。

图4.等转矩曲线 在进行矢量控制时，输入电流为以原点为中心的旋转矢量，因此，等转矩曲线的相切圆半径就是当前转矩条件下的最小电流，以及最合理的$i_d$、$i_q$组合。如图5所示，与转矩相切的圆表示想要达到当前转矩需要的最小电流，而从原点指向相切点的矢量就是输入电流矢量，该矢量向横坐标投影即为d轴电流，向纵坐标投影即为q轴电流。

图5.等转矩条件下的最小电流 我们把不同转矩的相切点连接起来，就构成了任意转矩下的最小输入电流，也就完成了MTPA的曲线绘制，如图6所示。

图6.MTPA

在工程应用中，常常将不同转矩对应的$i_d$、$i_q$制表，通过查表法完成MTPA输出，很大程度上节约了计算资源。要注意的是，实际应用时，逆变器电流不可能无限制增大，所以，MTPA曲线受到电流极限圆的限制，也比较容易理解，假设逆变器可承受的电流为$i_m$，那么，$i_d$、$i_q$要满足：$$\sqrt{i_d^2+i_q^2}\le i_m$$如图7所示，在电流极限圆约束下，MTPA有效部分为极限圆内绿色曲线

图7.电流极限圆

除了电流约束条件外，电压也会对电机运行过程产生约束，dq轴电压方程为$$\{\begin{array}{c}{u}_d=R{i}_d+L_d\frac{d{i}_d}{dt}-\omega L_q{i}_q\\ \\ u_q=R{i}_q+L_q\frac{d{i}_q}{dt}+\omega (L_d{i}_d+{\psi }_f)\end{array}$$在稳态条件下，我们认为dq轴电流不再变化，同时由于绕组电阻很小，忽略其对dq轴电压的影响，原方程可以变化为：$$\{\begin{array}{c}{u}_d=-\omega L_q{i}_q\\ \\ u_q=\omega (L_d{i}_d+{\psi }_f)\end{array}$$假设逆变器给定的最大电压为$u_m$，电压约束条件为：$$u_d^2+u_q^2\le u_m^2$$$$(\omega L_q{i}_q{)}^2+{\omega }^2(L_d{i}_d+{\psi }_f{)}^2\le u_m^2$$$$(L_q{i}_q{)}^2+(L_d{i}_d+{\psi }_f{)}^2\le (\frac{u_m}{\omega }{)}^2$$可以看出电压约束条件为椭圆，椭圆的中心点为$(-\frac{{\psi }_f}{\omega },0)$，且对于不同的转速，电压极限圆也不同，随着转速增加，电压极限圆不断缩小。如图8所示。

图8.电压极限圆

电机运行过程必然要同时受到电压极限圆和电流极限圆的约束，例如图8中B点，若想要恒转矩输出15N·m的力矩，能够允许的最大速度是3500RPM，因为在3500RPM速度时，母线电压已经达到极限了，可以理解为方波控制中PWM输出已经达到100%，而当电机速度低于该速度时，可以通过调制母线电压大小达到控制转速的目的，用公式更容易理解些：把电压极限圆的公式稍稍改动：$$(L_q{i}_q{)}^2+(L_d{i}_d+{\psi }_f{)}^2=(\frac{u}{\omega }{)}^2$$把最大电压$u_m$改变为实时母线电压$u$，中间的不等号变成等号，可以看出来，当MTPA输出恒定转矩时，$iq、id$固定不变，母线电流不变，电压与转速的比值不变，因此，想要速度增大，提高母线电压就可以。当母线电压提高到最大电压时，就不能再通过MTPA提速了。想要得到更大的转速只能通过弱磁的方式，因此，B点对应的速度也叫转折速度，所有的MTPA曲线、等力矩线、电压极限圆交点都是转折速度点。有一个特殊的转折速度点，就是图8中的A点，当速度小于A点速度时，电机能够恒最大转矩运行，当速度大于A点速度时，电机能够恒最大功率运行，这个速度点就是基速。
需要注意的是，这里提到的恒转矩并不是任何负载条件下都输出相同的转矩，回忆一下电机的运动方程$$T_e=T_L+B\omega +J\frac{d\omega }{dt}$$稳态条件下，电机提供多少转矩与负载大小息息相关，我们说的恒转矩是指在一定的速度范围内，随着速度变化，输出的转矩恒定，就像我们乘坐的电梯，从关上门的那一刻，负载就固定了，电机输出多少转矩也固定了，不论电梯以多快的速度运行，他都要输出固定的转矩。
恒功率运行容易理解些，因为此时电压与电流均已到达极限，功率不会再变了，在弱磁控制中，再详细说明等功率运行过程。

4、弱磁控制

在MTPA中已经提到了超过转折速度要弱磁了，弱磁提速的定性理解就是，为了保证反电势不大于输入电压，在反电势正比于转速与磁链的乘积的条件下，尽可能减小磁链，从而获得更高的速度，定量的理解还是电压极限圆那个公式，因为要进行弱磁时，母线电压已经达到电压极限，此时若能够反向增加id电流，电压与转速的比值将会降低，而电压固定的，所以转速会增加。
$$(L_q{i}_q{)}^2+(L_d{i}_d+{\psi }_f{)}^2=(\frac{u}{\omega }{)}^2$$现在我们通过两种不同的情况来了解弱磁控制。如图9所示。

图9.弱磁 当前工作点为B时，此时进行弱磁工作点将按照蓝色箭头方向移动，电机仍然可以工作在恒转矩模式，因为在B点虽然电压已经达到极限，但显然，电流仍然有很大的调整空间，伴随着id反方向增大，iq减小，总电流增大，此时电压与转速比值减小，电压不变，转速提高。 当前工作点为A时，此时进行弱磁工作点将按照红色箭头方向移动，电机工作在恒功率模式，因为在A点电压和电流都已经达到极限，此时功率为恒定值，功率为转速与转矩的乘积，因此，在这一阶段速度升高转矩就会降低，相反，转矩升高速度一定下降。

5、MTPV控制

实际上，从A工作点开始进行的弱磁并不会沿着电流极限圆一直走，因为在C点处有更好的控制方式，能够充分发挥电机的潜能，这就是MTPV，如图10中的粉色粗虚线，与MTPA相似，这条曲线是等转矩曲线与电压极限圆相切点的连线，连线上的点代表着相同转矩下产生最大速度的点，也是相同速度下产生最大转矩的点。因此，当弱磁进行到C点（MTPV、电流极限圆、等转矩曲线交点），可以沿着MTPV曲线向电压极限圆圆心移动，此时速度不断提升，输出的转矩为当前速度下能够产生的最大转矩。
从B工作点开始进行的弱磁也是同样，当弱磁沿着等力矩曲线移动到与MTPV曲线交叉点时，开始沿着MTPV曲线移动，从而在继续升速的同时产生相对较大的力矩。

图10.MTPV

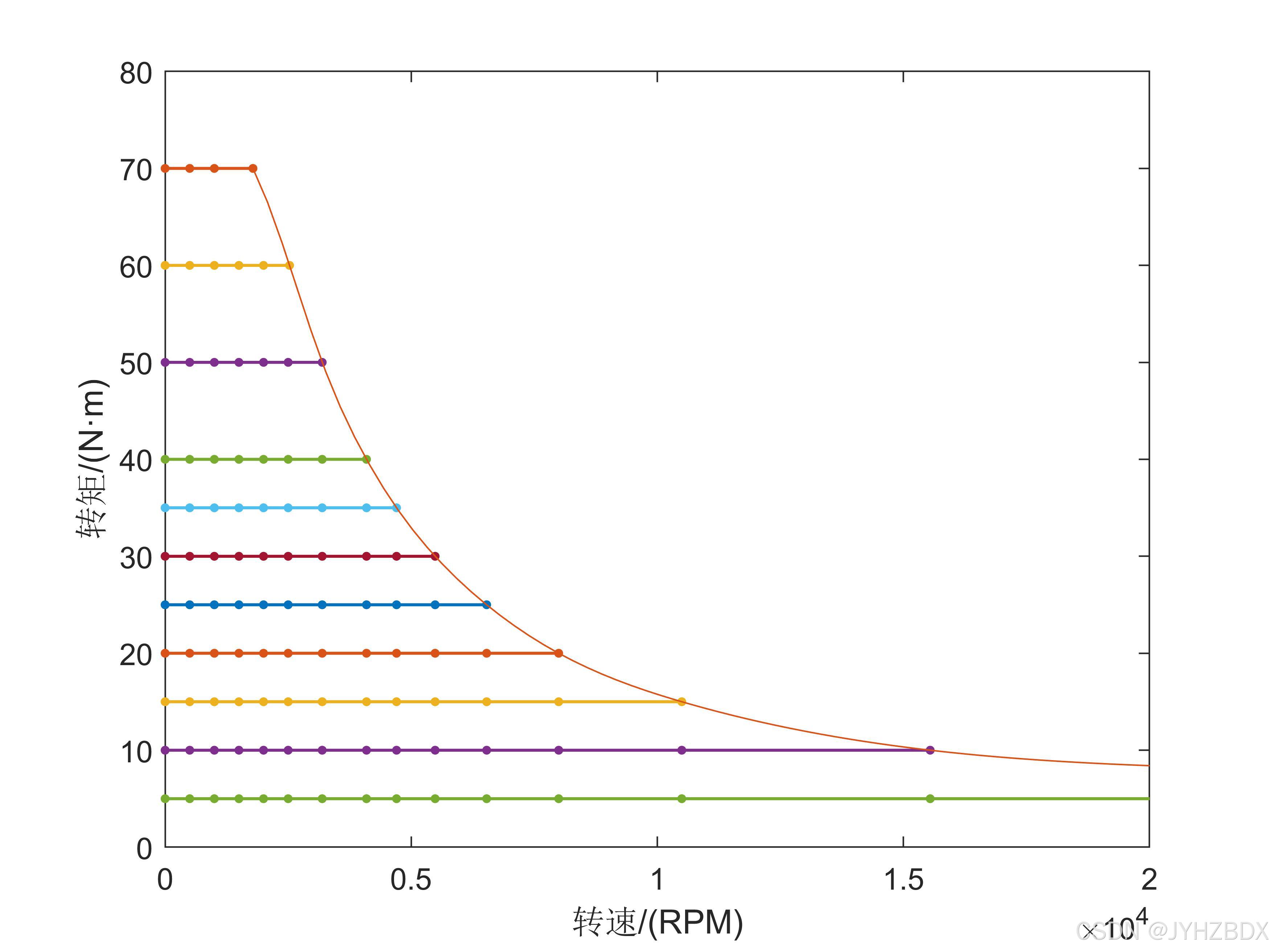
6、n-T图

根据上述转矩、转速的关系绘制出nT图