原码、补码以及定点数运算

CuteBaBaKiller

已于 2022-09-26 14:51:55 修改

阅读量3.2k

点赞数 3

分类专栏： IC逻辑文章标签：补码定点数饱和截位

于 2022-07-19 15:33:40 首次发布

本文链接：https://blog.csdn.net/Jackiezhang1993/article/details/125785080

版权

IC逻辑专栏收录该内容

7 篇文章 16 订阅

订阅专栏

1 进制相互转换

1.1 十进制转换二进制

十进制数转换为二进制数时，由于整数和小数的转换方法不同，所以先将十进制数的整数部分和小数部分分别转换后，再加以合并。

1.1.1 整数部分

十进制整数转换为二进制整数采用"除2取余，逆序排列"法。

具体做法是：用2整除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为小于1时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。

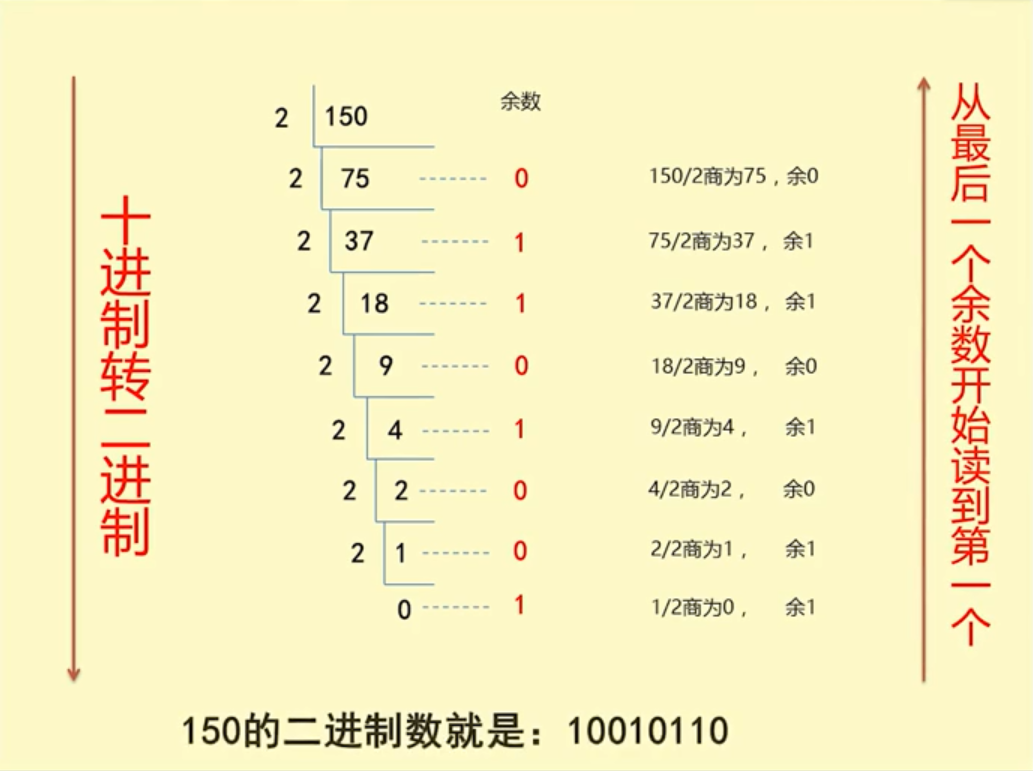
1.1.2 小数部分

十进制小数转换成二进制小数采用"乘2取整，顺序排列"法。

具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，此时0或1为二进制的最后一位。（或者达到所要求的精度为止）

1.2 二进制转换十进制

1.2.1 转换方法

二进制数转换成十进制数采用“权相加”法，举例如下：

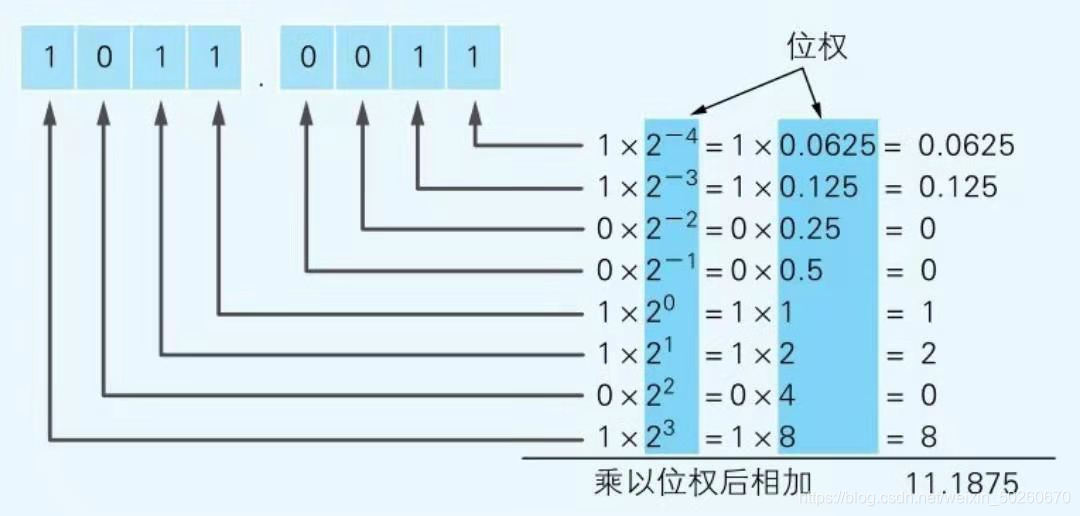
在这里插入图片描述

2 原码、反码与补码

2.1 模(mod)的概念

“模”指一个计量系统的计数范围。例如：

①时钟的计量范围是0~11，模=12；

②表示n位的计算机的计量范围是0~ $2^{n}$ -1，模= $2^{n}$ 。

“模”实质上是计量器产生“溢出”的量，它的值在计量器上表示不出来，计量器上只能表示出模的余数。任何有模的计量器，均可化减法为加法运算。

2.2 True Form（原码）

原码是一种计算机中对数字的二进制定点表示方法。原码表示法在数值前面增加了一位符号位（即最高位MSB/Most Significant Bit为符号位）：正数该位为0，负数该位为1（0有两种表示：+0和-0）。

n+1位有符号数表示的范围为- $2^{n}$ 至 $2^{n}$ -1，其中：

①原码+0为十进制0，原码-0为十进制- $2^{n}$ ；

②最高位为0且其他位不全为0的表示正数；

③最高位为1且其他位不全为0的表示负数。

2.3 Complement Code

2.3.1 反码（1's Complement Code、1的补码）

①正数的反码与原码相同；

②负数的反码是原码的符号位不变，其余剩下各位按位取反。

2.3.2 补码（2's Complement Code、2的补码）

将指向8点的时钟拨到6点有以下2种方法：一是倒拨2小时，即8-2=6；另一种是顺拨10小时，8+10=12+6。在模=12的系统里，2与10互为补数，加10和减2效果是一样的，因此凡是减2运算，都可以用加10来代替。

对于计算机，其概念和方法完全一样。n位计算机，设n=8，能表示的最大数是11111111，若再加1成100000000(9位)，但因只有8位，最高位1自然丢失（相当于丢失一个模）。又回到 00000000，所以8位二进制系统的模为 $2^{8}$ 。这样的系统中减法问题也可以化成加法问题。

在计算机系统中，数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统一处理；同时，加法和减法也可以统一处理。

定义：对于(n+1)bits的正数X，[-X]的补码等于mod-X = $2^{n+1}$ -X的值。

原码、补码互相转换：

①原码转换为补码：

正数的补码与原码相同，±0的补码都是+0；

负数的补码是原码的反码加1。

②补码转换为原码：(补码的最高有效位MSB看做符号位Sign Bit，0代表正数，1代表负数。)

如果补码的符号位为“0”，表示是一个正数，其原码就是补码；

如果补码的符号位为“1”，表示是一个负数，那么求给定的这个补码的补码就是其原码。

原码		111	110	101	100	000	001	010	011
真值	-4	-3	-2	-1	-0	+0	+1	+2	+3
补码	100	101	110	111	000		001	010	011

补码的运算：

对于一个n+1位的有符号正数X，有如下关系：

X补 + (-X)补 = 100...0(n+1个零,刚好溢出) = $2^{n+1}$ (模的概念)

所以假设寄存器是n+1位的，那么-X的补码应该是 $2^{n+1}$ -X 的二进制编码。

3 二进制运算

3.1 加减法

a-b=[a]补+[-b]补=[a+(mod-b)]运算中视为无符号数且结果为补码

其中a、b为有符号的正数。

有符号数相加减：将原码加减法转换为补码的加法（这里看做无符号数直接相加），最后将补码形式的结果再转换回原码。

例如：2 - 3 = 0010 - 0011 = 2 + (-3) = 0010 + 10000(模) - 0011

= 0010(补) + 1101(补)

= 1111(补) = 1001(原) = -1

3.2 左移

乘以2的次幂：采用左移，移动后空出来的最低位补0。

无论是正负原码还是补码都可以采用左移，且补码左移后需要再求回原码。

	原码	补码
初始值	1010 = -2	1110(补)
左移2位（乘以4）	101000 = -8	111000(补) = 101000(原) = -8

3.3 逻辑右移与算数右移

逻辑右移，高位补0。

算术右移，高位补同符号数。

正/负数	99 = [0110 0011]原	-21 = [1001 0101]原 → [1110 1010]反 → [1110 1011]补
右移	逻辑右移>>4	算数右移>>4	逻辑右移>>4	算数右移>>4
操作	[0000 0110]原 = 6 = 99/(2^4) （向下取整）	[0000 1110]补 → [0000 1110]原 = 14	[1111 1110]补 → [1000 0001]反 → [1000 0010]原 = -2 （向下取整）
判断	正确	错误	正确

正/负数

99 = [0110 0011]原

-21 = [1001 0101]原 → [1110 1010]反 → [1110 1011]补

右移

逻辑右移>>4

算数右移>>4

逻辑右移>>4

算数右移>>4

操作

[0000 0110]原 = 6 = 99/(2^4) （向下取整）

[0000 1110]补 → [0000 1110]原 = 14

[1111 1110]补 → [1000 0001]反 → [1000 0010]原 = -2

（向下取整）

判断

正确

错误

正确

总结：有符号数采用补码算数右移；无符号数直接逻辑右移。

4 定点数

4.1 定义

定点数格式为： <#bits,#interger_bits,sign_format>

其中：

①#bits：表示整个定点数的总位宽，包括整数部分的bit位数、小数部分的bit位数和1bit位宽的符号位（无符号数时，无符号位）；

②#interger_bits：表示定点数的整数部分的bit位宽（不包含符号位）；

③sign_format：表示定点数的类型，U表示无符号数，T表示有符号数（补码形式）。

举例：对于定点数<8,2,t>的二进制数01000100，最高位为0表示为正数，10为整数位表示为2，00100为小数部分表示为0.125，故概述为2.125。

4.2 定点数的处理

4.2.1 无符号数相加

①分为整数部分和小数部分，位宽短的分别补0对齐位宽。

②分别在最高位加1bit整数位0用来进位。

<m,n,u> + <x,y,u> = <max(n,y)+max(m-n,x-y)+1, max(n,y)+1, u >

当两个相同的无符号数相加时：

<m,n,u> + <m,n,u> = <m+1 , n+1 , u >

4.2.2 有符号数相加

①小数点前位宽短的补“符号位”，小数点后位宽短的补0。

②分别对两个加数在最高位加1bit同符号位，用来整数进位。

<m,n,t> + <x,y,t> = <max(n+1, y+1)+max(m-1-n, x-1-y)+1, max(n,y)+1, t >

当两个相同的有符号数相加时：

<m,n,t> + <m,n,t> = <m+1 , n+1 , t >

4.2.3 无符号数相乘

<m,n,u> * <x,y,u> = <m+x, n+y, u>

4.2.4 有符号数相乘

<m,n,t> * <x,y,t> = <m+x-1, n+y, t>

4.2.5 无符号数与有符号数运算

有符号数和无符号数的混合运算中，先把无符号数转换为有符号数，即加1bit符号位“0”，然后按照有符号数处理。

5 饱和截位

5.1 对于无符号数

无符号数的饱和截位就是看一下截位前数据是否超过截位后允许的最大值，如果超过了就把它饱和到最大值，否则直接截位。举例说明下：

如果要将<m,n,u>饱和截位为<x,y,u>，即要对filter_sum[m-1:0]的高(n-y)bit进行饱和判断，对低((m-n)-(x-y))bit进行截位，所对应的RTL code如下所示：

if(~|filter_sum[m-1:m-(n-y)])                     //判断高位是否为全零

    data_q<=filter_sum[m-(n-y)-1:((m-n)-(x-y))];  //全零则直接截位

else if                                                                

    data_q<=x'b0-1'b1;                            //非全零则饱和到最大值

5.2 对于有符号数

注意：对于有符号数，均以补码的形式来表示和计算。

5.2.1 先进行非对称饱和截位

对有符号数的非对称饱和截位，即：判断数据是否超过最大正值，如果超过了就把它饱和到最大正值，再判断数据是否超过最大负值，如果超过了就把它饱和到最大负值，否则直接截位。举个例子说明下：

如果要将<27,16,t>饱和截位为<16,10,t>，即要将filter_sum[26:0]的高6bit饱和掉，对低5bit进行截位：

if((~|filter_sum[26:20]) || (&filter_sum[26:20]))//判断高位(包含符号位)是否全0或全1
    data_q<=filter_sum[20:5];//没有超出范围,直接截位(filter_sum[20]与[26]相同)
else if(~filter_sum22_i[26])
    data_q<=16'h7FFF;//符号位为0正且超出范围,直接饱和最大正值
else
    data_q<=16'h8000;//符号位为1负且超出范围,直接饱和最小负值

(最大正值 16'h7fff + 1'b1变成最小负值16'h8000。)

5.2.2 再进行对称饱和操作

位宽不变化且没有截位，只有饱和操作。举个例子，如果是3bits的有符号数，那么就是将数的表示范围从<-8,7>限定为<-7,7>，这样做的目的是为了让固定位宽能表示相反的数组，例如-8即无法取反到+8，因为超出表示范围。

如果data_out_q为16bits的有符号数，那么该饱和操作就应该为：

data_out_q <= (data_q[15:0] == 16'h8000) ? 16'h8001:data_q;

CuteBaBaKiller

关注

3
点赞
踩
17

收藏

觉得还不错? 一键收藏
9
评论
原码、补码以及定点数运算

定点数格式为其中表示整个定点数的总位宽，包括整数部分的bit位数、小数部分的bit位数和1bit位宽的符号位（无符号数时，无符号位）；表示定点数的整数部分的bit位宽（不包含符号位）；表示定点数的类型，U表示无符号数，T表示有符号数（补码形式）。举例对于定点数的二进制数01000100，最高位为0表示为正数，10为整数位表示为2，00100为小数部分表示为0.125，故概述为2.125。...............
复制链接

扫一扫