| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 13323 | Accepted: 4675 |
Description
In a certain course, you take n tests. If you get ai out of bi questions correct on test i, your cumulative average is defined to be
 .
.
Given your test scores and a positive integer k, determine how high you can make your cumulative average if you are allowed to drop any k of your test scores.
Suppose you take 3 tests with scores of 5/5, 0/1, and 2/6. Without dropping any tests, your cumulative average is  . However, if you drop the third test, your cumulative average becomes
. However, if you drop the third test, your cumulative average becomes  .
.
Input
The input test file will contain multiple test cases, each containing exactly three lines. The first line contains two integers, 1 ≤ n ≤ 1000 and 0 ≤ k < n. The second line contains n integers indicating ai for all i. The third line contains n positive integers indicating bi for all i. It is guaranteed that 0 ≤ ai ≤ bi ≤ 1, 000, 000, 000. The end-of-file is marked by a test case with n = k = 0 and should not be processed.
Output
For each test case, write a single line with the highest cumulative average possible after dropping k of the given test scores. The average should be rounded to the nearest integer.
Sample Input
3 1 5 0 2 5 1 6 4 2 1 2 7 9 5 6 7 9 0 0
Sample Output
83 100
题意:
给你n组数,每组数中有两个数a[i]和b[i],让你在这n组数中选出n-k组使得100*∑a[i]/∑b[i]值最大
经典01分数规划问题:
http://blog.csdn.net/jaihk662/article/details/77505318
还是这个公式,x[i]表示选还是不选
先给出二分思路:
二分cnt,然后求出所有的d[i],按d[i]从大到小排序选择前n-k个并求和,如果大于0说明可能不是最优解
再说Dinkelbach算法:
先随机一个cnt,然后求出所有的d[i],按d[i]从大到小排序选择前n-k个求出∑a[i]/∑b[i],如果∑a[i]/∑b[i]==cnt,那么说明是最优解,否则令cnt=∑a[i]/∑b[i]继续,直到求出最优解(一般优于二分)
其实这题还有一个贪心思路:算出所有的d[i] = a[i]/b[i],也就是比率,然后按这个从大到小排序,选最大的k个
但这是错的,一个很简单的反例:
3 1
100 1 100
100 5 200
正确答案应该是(101/105)*100 ≈ 96
#include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
typedef struct Res
{
double a, b;
double d;
bool operator < (const Res &b) const
{
if(d>b.d)
return 1;
return 0;
}
}Res;
Res s[1005];
int main(void)
{
int i, n, k;
double cnt, sa, sb;
while(scanf("%d%d", &n, &k), n!=0 || k!=0)
{
k = n-k;
for(i=1;i<=n;i++)
scanf("%lf", &s[i].a);
for(i=1;i<=n;i++)
scanf("%lf", &s[i].b);
cnt = 0;
while(1)
{
for(i=1;i<=n;i++)
s[i].d = s[i].a-cnt*s[i].b;
sort(s+1, s+n+1);
sa = sb = 0;
for(i=1;i<=k;i++)
{
sa += s[i].a;
sb += s[i].b;
}
if(fabs(sa/sb-cnt)<0.00001)
break;
cnt = sa/sb;
}
printf("%.0f\n", cnt*100);
}
return 0;
}







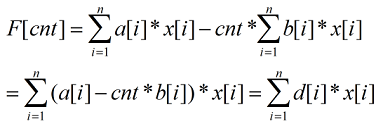














 4455
4455

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








