伽马函数：
其中其中参数
\Gamma (\alpha) = \int_{0}^{+\infty}x^{\alpha - 1}e^{-x}dx，为伽马函数，其中参数\alpha >0.
特殊函数入门指南——伽马函数(一) - 知乎 (zhihu.com)
首先伽马函数有如下性质：
\Gamma (\alpha +1) = \alpha \Gamma (\alpha )
证明：
\Gamma (\alpha +1) = \int _{0}^{\infty}x^{\alpha }e^{-x}dx=-e^{-x}x^{\alpha }|_{0}^{\infty}+\int_{0}^{\infty}\alpha x^{\alpha -1}e^{-x}=0+\alpha \int_{0}^{\infty} x^{\alpha -1}e^{-x}=\alpha \Gamma(\alpha )
当\alpha 为自然数n时，有\Gamma (n+1)=n\Gamma(n)=n!
当为自然数n时，有
幂函数与指数函数的乘积求积分，该如何实现？
6月14日学习日记：伽马函数在二分之一处取值的几种计算方式 - 知乎 (zhihu.com)
这个作者解决了。
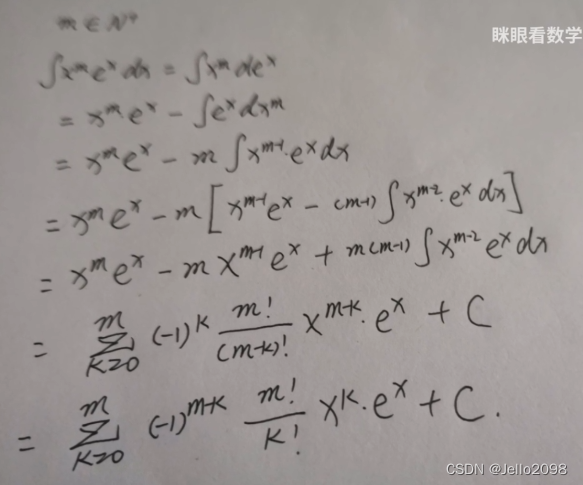
此时换元，令x = x^2
4750
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
