贝叶斯估计学习中的小趣
–我的学习笔记1
小引入:嗯,某人甲向10个女生告白,告白成功的次数,那甲的外貌以及情商各综合方面打分多少?
嗯,同样的,甲向100个女生告白,噢不,太夸张了,改为50个吧,告白成功的次数,那甲的外貌以及情商各综合方面打分多少?(ps:忽略女生外貌对某甲的影响,假设他都会尽心去告。白。)
要对甲综合“能力”打分,经典的概率派会直接说,唉,极大似然估计得,给你满分100%,或者99%,那时候太年轻,永远是概率和频率傻傻分不清~
巴特!贝叶斯派可不是这么做的喔,首先,他们不认为概率和频率是一样的,主观的概率和实体概率可以互相转化~
我不管,反正他们就是用不同的手段去衡量那个甲的ability的。
- 从有趣的历史开始入手吧(虽然我手法粗涩)
从前的从前,自统计学有了以后,便渐渐形成了两大学派,分别是概率派和贝叶斯派。
那么,这两派之间究竟都在做着什么事儿呢?简单地说,概率派做的事便是从“自然”角度出发,试图直接为“事件”本身建模,即事件A在独立重复试验中发生的频率趋于极限p,那么这个极限就是该事件的概率。比如说,想要计算抛掷一枚硬币时正面朝上的概率,我们需要不断地抛掷硬币,当抛掷次数趋向无穷时正面朝上的频率即为正面朝上的概率。
和概率派相对不同的是,在贝叶斯框架下,同一件事情对于知情者而言就是“确定事件”,对于不知情者而言就是“随机事件”,随机性并不源于事件本身是否发生,而只是描述观察者对该事件的知识状态。那么,再以上面例子作解,则想要计算抛掷一枚硬币时正面朝上的概率,假设我们第一次,第二次,直到第n次投掷了硬币,是正是反,我们对投出正的概率一无所知,设概率为A,在这种场合下,贝叶斯等人会采用“同等无知”的原则先投掷,然后使用(1,0)上的0-1分布作为某A的先验分布,即贝叶斯假设,然后再利用贝叶斯公式,求出A的后验分布。 - 第一步,了解下贝叶斯估计
其实嘛,它无非就是简单的6步骤搞定:
其实我“醉翁之意不在酒,在乎山水之间也”( •̀ ω •́ )y
那本我们学习的教材书[概率论与数理统计教程.茆诗松等编写]里面,在讲贝叶斯估计的看例子时,提到的方法是相对复杂的,就比如以下例(在老师的ppt截图)
这样做法挺好,不过有一点可以做优化,那步小优化,就是我稀饭这里一个小小的优化“程序”。
在这里,先引进来一个新的概念,核函数(RBF)。核函数表示了两个数据之间的相似性,在一个新高度上进行运算。科科,以下便是百度词条对核函数的新评:
1)核函数的引入避免了"维数灾难",大大减小了计算量可以有效处理高维输入。
2)无需知道非线性变换函数Φ的形式和参数.
噢,不对,先来个例子可能就get了。
在数理统计中,到达一个高度的计算式子通常都会比较长,自带系数略多,这个方法真真赞,将核函数植入以上例题,在求后验分布时可以省略x的系数~
神奇地,还有看到一个超级完整的关于正态分布贝叶斯分类的完整code,我果断收藏了,发现运作了之后可以出现超好看的图喔,以下那个链接便是code。它不仅有样本分类而且会在二维坐标系下画出,正确分类与错误分类的点都会有不同的标志。反正这一部分是涉及到贝叶斯决策滴,还是一个大大的学问呢。
http://www.cnblogs.com/tiandsp/archive/2012/05/18/2508384.html











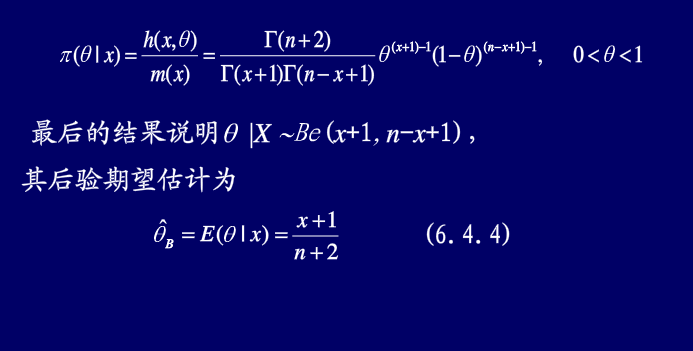


















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








