迟分是什么，不是什么【下篇】

最新推荐文章于 2025-05-05 13:07:46 发布

Jina AI

最新推荐文章于 2025-05-05 13:07:46 发布

阅读量949

点赞数 11

文章标签：人工智能深度学习机器学习

本文链接：https://blog.csdn.net/Jina_AI/article/details/142934173

版权

本篇文章主要是把迟分策略里容易混淆的概念和对比再详细讲讲，强烈建议各位先去看看上一篇：【上篇】长文本 Embedding 模型中的“迟分”策略。

建议阅读顺序：上篇、下篇、研究论文: https://arxiv.org/abs/2409.04701/

把长文档切块，这其中有两个关键问题：

首先，边界断点怎么定？

你可以用固定长度的 Token，或者固定数量的句子，再高级点的就用正则表达式或者语义分割模型，比如 https://jina.ai/segmenter/。

文本块分割得准不准，这不仅关系到搜索结果好不好读，还关系到做 RAG 的时候，给 LLM 喂进去的文本块是不是正好，不多不少。

另外，每个分块里的上下文信息容易丢失。

文档切完之后，很多人下一步就是把每个分块拿去批量向量化。但这么做容易把原文档里的全局上下文信息给丢了。

之前不少研究都是先解决第一个问题，觉得边界检测做好了，语义表示自然就好了。比如说语义分块（Sementic Chunking），就是把向量空间里余弦相似度高的句子放一起，尽量保证语义单元的完整性。

但从我们 Jina AI 的角度来看，这两个问题基本是独立的，可以分开解决。非要分个轻重缓急的话，第二个问题，也就是上下文信息丢失的问题，更重要。

迟分解决上下文丢失问题

迟分（Late Chunking）主要就是解决第二个问题 —— 上下文丢失。它不是用来找最佳断点或者语义边界的。你该用正则表达式，启发式方法，或者其他技术来分块，还是得用。

但迟分不一样的地方是，它不是一切完就立马把每个块拿去向量化，而是先把整个文档在一个上下文窗口里编码了（插播广告：jina-embeddings-v3最新 SOTA 向量模型，支持 8192 Token 的长长长输入），然后再根据边界线索去进行均值池化操作。

所以你看这名字里带个“迟”字，就是这个意思，先向量化后分块。

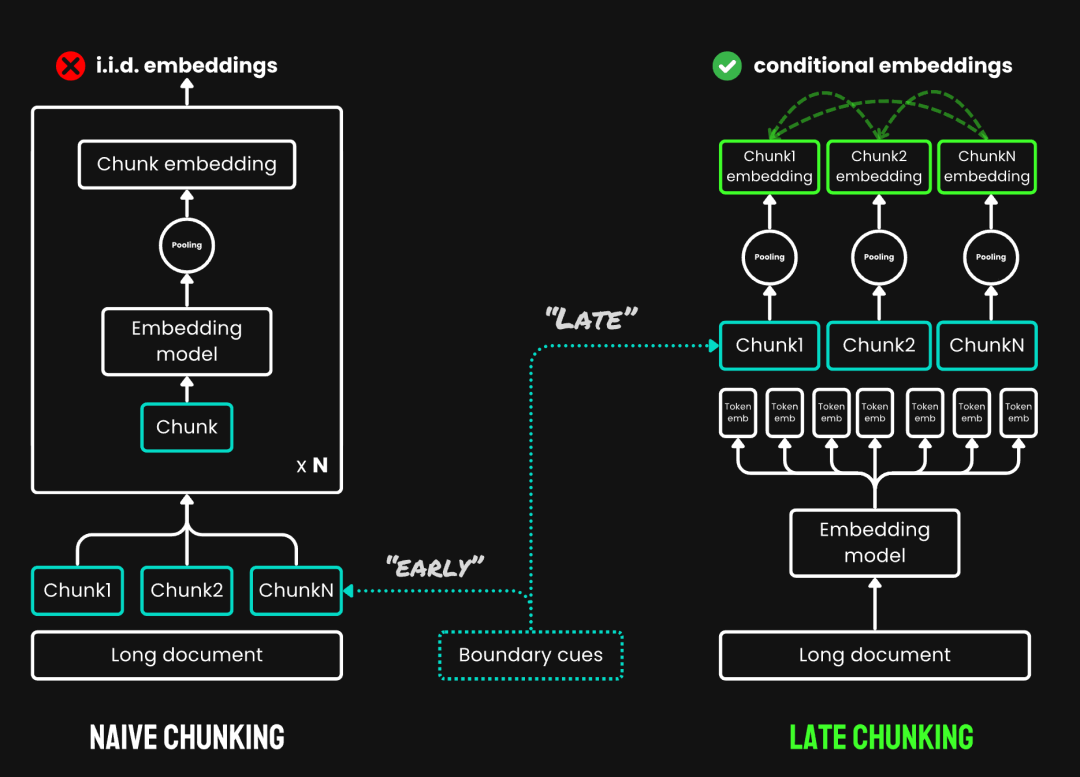
迟分也需要边界线索，但关键在于啥时候用这些线索。迟分是在整个文档向量完之后，才用边界线索来确定池化范围的。

迟分对边界线索不敏感

但有意思的是，我们从实验结果观察到，用上了迟分，对分块的要求就没那么高了。这就相当于部分解决了前面提到的第一个问题，也就是边界断点的问题。

说白了，就算你用简单的固定长度分块，配合上迟分，效果也能跟高级的边界检测算法不相上下。

我们 Jina AI 内部也测试过三种不同大小的向量模型，结果发现，迟分对所有模型、所有测试数据集都有稳定的提升效果。

话虽如此，向量模型本身仍然是最重要的因素，我们还没见过哪个用迟分的差模型，能比不用迟分的好模型效果更好。

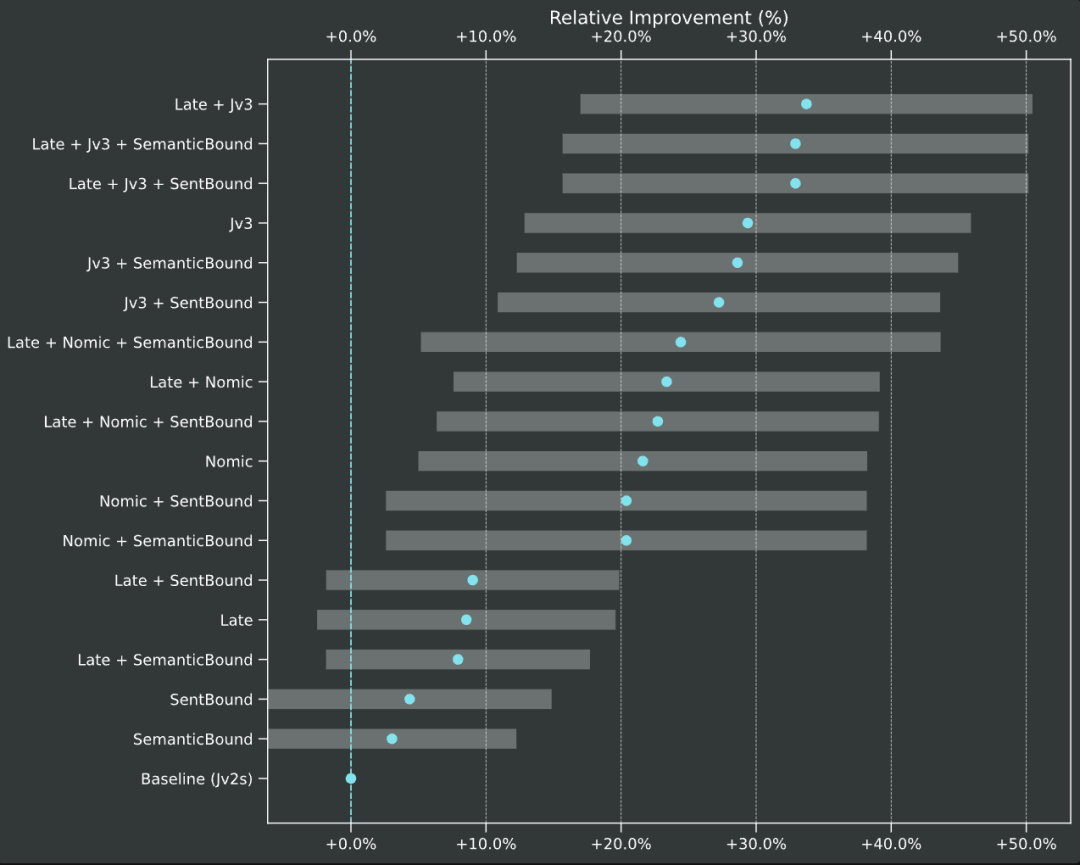
上图展示的是相对于 Baseline（即 jina-embeddings-v2-small，用的是固定长度的分割和朴素分块）的相对检索改进情况。

作为消融研究的一部分，我们测试了不同边界线索（固定标记长度、句子边界和语义边界）和不同模型（jina-embeddings-v2-small, nomic-v1, jina-embeddings-v3）下的迟分效果。

根据它们在 MTEB 上的表现，这三种向量模型的排名为：jina-embeddings-v2-small < nomic-v1 < jina-embeddings-v3。不过，本实验的重点不是评估向量模型本身的性能，而是看看更好的向量模型是怎么跟迟交互分块和边界线索相互作用的。

具体的实验细节，可以去看我们的研究论文：https://arxiv.org/abs/2409.04701

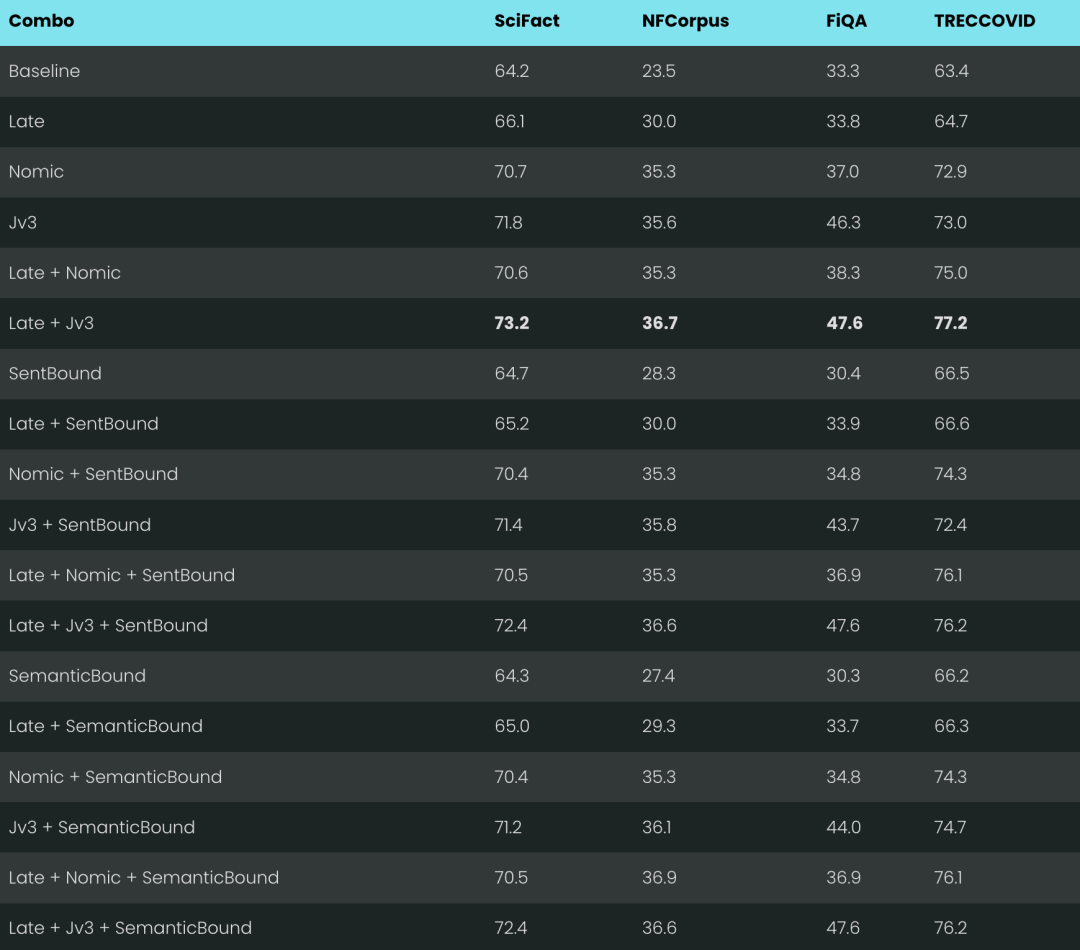
要注意，对边界线索不敏感，不代表我们可以完全忽略边界。边界对人的阅读，对 LLM 的推理都很重要。

我们是这样理解的：在优化分块的时候，也就是解决上面说的第一个问题的时候，我们可以完全专注于可读性，不用担心语义/上下文丢失的问题。因为迟分能搞定好的或者坏的边界断点，你关心可读性就好了。

迟分是双向的

另一个对迟分常见的误解是，迟分在生成文本块向量的时候，只考虑了前面的文本块，没“往后看”。这个理解不对。迟分的条件依赖其实是双向的，不是单向的。

这是因为向量模型（Encoder-only Transformer）里的注意力矩阵是全连接的，不像自回归模型里用的那种带掩码的三角形矩阵。

更正式地来说，文本块 k 的向量是：vₖ ∼ Q(cₖ∣D)，而不是 vₖ ∼ Q(cₖ∣c₁, c₂, ⋯, cₖ₋₁)，其中 Q 表示语言模型的因式分解。这也解释了为什么迟分对边界断点的精确性要求不高。

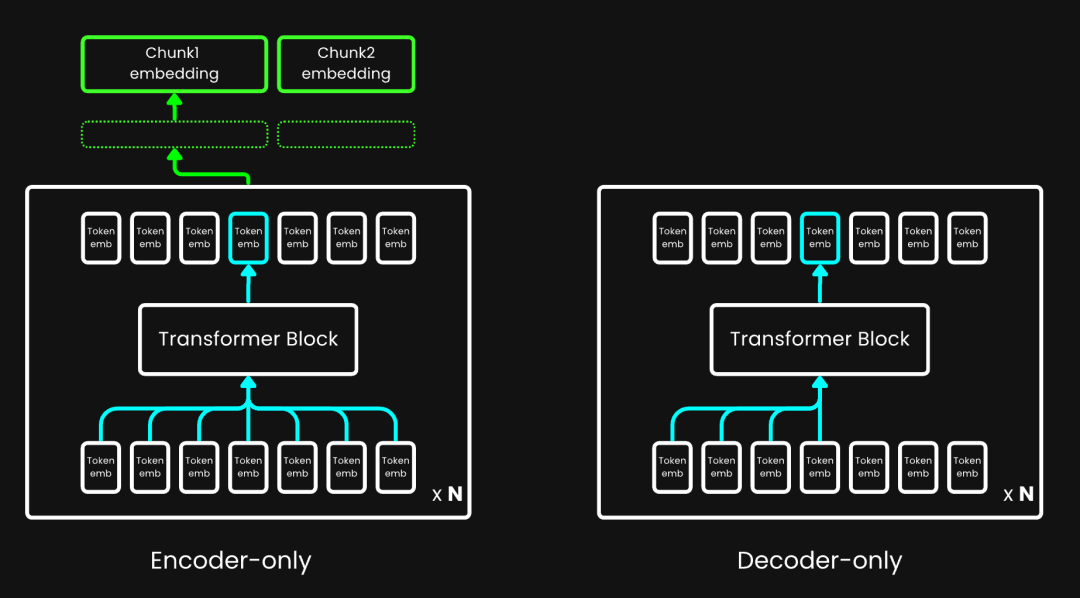
跟那种 Decoder-only，而且带掩码自注意力的模型不一样，向量模型一般是 Encoder-only，而且注意力矩阵是全连接的。也就是说，这意味着生成每个词的向量时，都会考虑同一上下文窗口内的所有其他词。

拿 jina-embeddings-v3 来说，这个窗口里最多能有 8192 Token。所以，迟分生成的文本块向量就携带了双向的全局上下文信息。

迟分可以训练

迟分不需要额外训练向量模型。任何使用均值池化的长文本向量模型都能用它，这对实际应用来说很方便。也就是说，如果你在做问答或者查询文档检索之类的任务，稍微微调一下还能提升性能。具体来说，训练数据得是这种格式的元组：

查询（比如问题或者搜索词）。
文档，包含回答查询需要的信息。
文档里的相关范围，也就是直接回答查询的那部分文本块。

训练的时候，用对比损失函数如 InfoNCE，把查询和文档的相关范围配对训练，这样就能保证相关跨度和查询在向量空间里靠得近，不相关的就离得远。最后模型就能学会在生成块向量的时候，更关注文档里最相关的部分。

详细内容可以看我们的研究论文：https://arxiv.org/abs/2409.04701

迟分 vs 上下文检索

迟分出来之后没多久，Anthropic 也做了个叫上下文检索的策略。Anthropic 的方法简单粗暴，直接用 LLM 来解决上下文丢失问题：

把每个文本块和整个文档一起喂给 LLM。
LLM 给每个文本块加上相关的上下文信息。
这样就能得到信息更丰富的向量。

在我们看来，这本质上就是上下文增强，用 LLM 把全局上下文显式硬编码到每个块里，成本、时间、存储空间都得考虑。而且，这方法对边界断点是不是敏感还不清楚，毕竟 LLM 得靠准确可读的文本块才能有效地丰富上下文。

相比之下，迟分对边界线索不敏感，前面也说了。它不需要额外的存储空间，因为向量向量的维度不变。虽然迟分用尽了向量模型的上下文长度，但它还是要比用 LLM 生成式地增强要快得多。

在我们研究论文的定性研究中，我们发现 Anthropic 的上下文检索的性能和迟分差不多。但迟分的解决方案更底层，更通用，也更自然，因为它利用了 Encoder-only Transformer 的内在机制。

哪些向量模型支持迟分？

迟分不是 jina-embeddings-v3 或者 jina-embeddings-v2 专属的。这个方法很通用，只要是使用均值池化的长文本向量模型都可以。比如说，我们在这篇文章里就展示了 nomic-v1 也能用。我们也热烈欢迎所有向量模型的提供商都实现对迟分的支持。

如果你是一个模型用户，想看看某个新的向量模型或者 API 支不支持迟分，可以按这几个步骤来：

单一输出: 这个模型是不是对每个句子只给一个最终的向量？如果是对每个词都给一个向量，那它很可能不支持迟分。
长文本支持: 这个模型能不能处理至少 8192 Token 的上下文？如果不能，那迟分就没法用，或者更准确地说，给短文本模型用迟分没啥意义。如果能，你得确保它在长文本上的效果确实好，别光说支持，实际表现不行。一般你可以在模型的技术报告里找到这方面的信息，比如在 LongMTEB 或者其他长文本基准测试上的评估结果。
均值池化: 对于那些在池化之前提供词级别向量的自托管模型或者模型 API，你得看看它默认的池化方法是不是均值池化。用 CLS 或者 MAX 池化的模型跟迟分不兼容。

总而言之，如果一个向量模型支持长文本，而且默认用均值池化，那它就能轻松支持迟分。可以去看看我们的 GitHub 仓库，里面有详细的代码实现和讨论。

https://github.com/jina-ai/late-chunking/issues/