模型的分类与对比

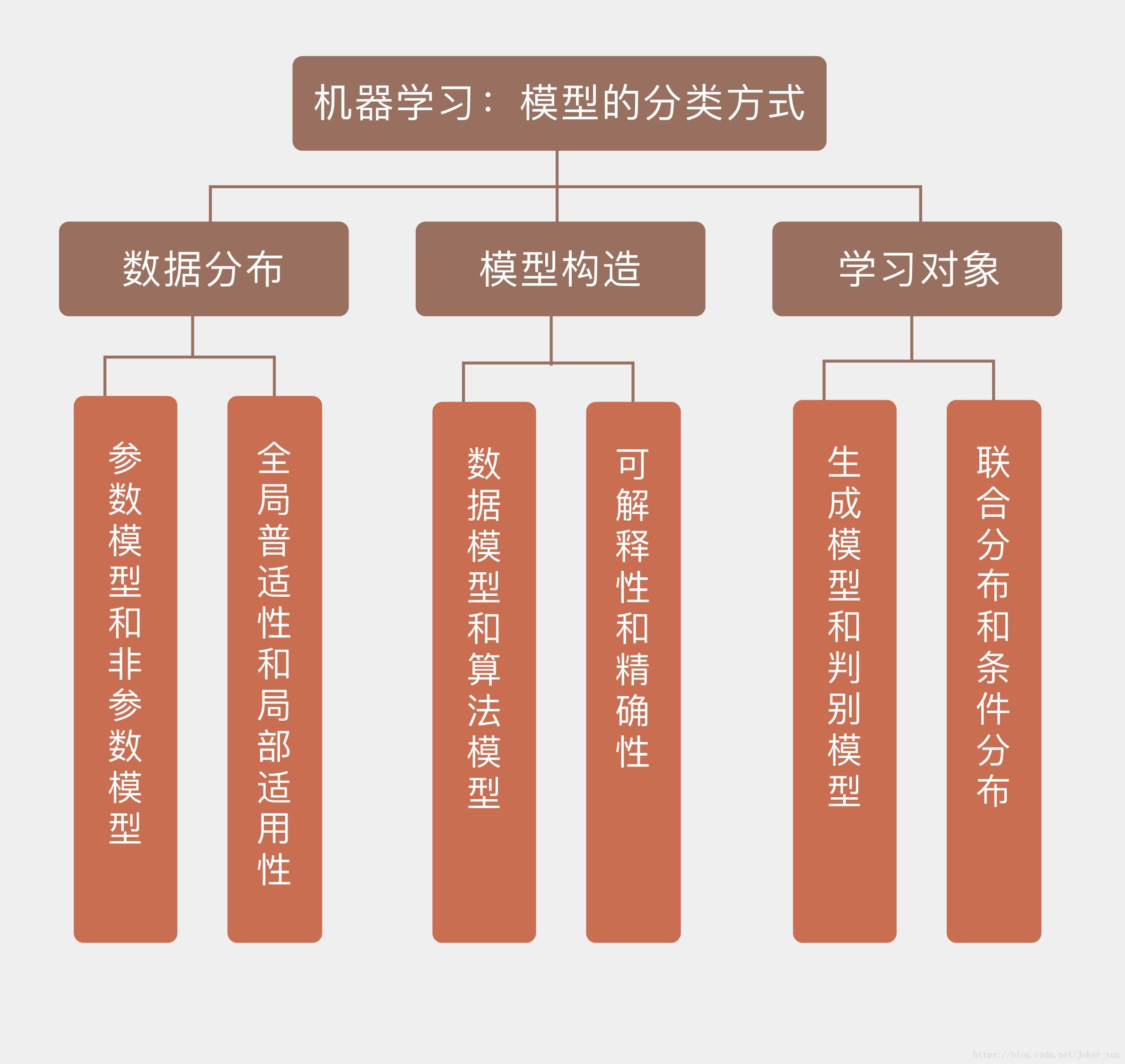
从学习方法角度进行划分

参数模型 vs 非参数模型：全局普适性 vs 局部适用性

❶ 参数模型

“新闻总是抄袭历史，模式在深处等待发掘。“

当我们对问题有认知，有了「定性」的判断，然后我们便可以用「定量」的方式将它们刻画出来。所谓“参数模型”。

优点：简单，只需付出较小的计算代价就可以从假设空间中习得一个较好的模型

缺点：其可用性却严重依赖于先验知识的可信度，但若先验分布错误，则无法学出好的结果。

❷ 非参数模型

“知之为知之，不知为不知，是知也。”

当我们对问题知之甚少，最好的办法反而是避免对潜在模型做出过多的假设，所谓“非参数模型。”

优点：当训练数据趋于无穷多时，非参数模型可以逼近任意复杂的真实模型。

缺点：和参数相比，非参数模型的时空复杂度都会比参数模型大得多。

误区：“非参数模型”不是“无参数模型”，恰恰相反，非参数模型意味着模型参数的数目是不固定的，并且极有可能是无穷大，这决定了非参数模型不可能像参数模型那样用固定且有限数目的参数来完全刻画。

❸ 参数模型 vs 非参数模型

例子： 假定一个训练集中有 99 个数据，其均值为 100，方差为 1。那么对于第 100 个数据来说，它会以 99% 的概率小于哪一个数值呢࿱