从手动到自动：基于PLECS+Matlab的BUCK电路PID参数整定方法

其优势在于无需依赖先验理论模型，可直接从工业过程控制、电力电子系统（如开关电源环路分析）或机电设备的实测数据中提取动态特性，生成高拟合度（NRMSE >90%）的Simulink兼容模型或嵌入式代码，为控制器设计、系统仿真与实时部署提供高效解决方案，尤其适用于理论建模困难或含强非线性环节的复杂系统。

实际使用过程中，拟合的传递函数精度常常能达到 99% 以上。

详细内容可移步：MATLAB系统辨识工具箱介绍（完结）

（2）sisotool控制系统设计工具简介

MATLAB中的SISO Tool（sisotool）是一款专用于单输入单输出（SISO）控制系统设计的交互式工具，支持基于频域/时域响应的控制器参数整定与系统性能分析。

用户可通过图形化界面实时调整补偿器（如超前滞后网络、PID）的零极点位置或频域特性（增益/相位裕度），同步观察根轨迹、波德图、阶跃响应及奈奎斯特曲线的变化，实现闭环稳定性与动态性能（超调量、调节时间）的快速优化。

该工具内置自动调参算法，兼容传递函数、状态空间模型及Simulink模块，支持从工业控制器（如电机调速、开关电源环路补偿）到航空航天系统的设计场景，其直观的可视化反馈与多目标约束分析能力，显著降低了复杂控制结构（如级联控制、多回路系统）的调试难度，并可生成C代码或直接导出至实时硬件平台，实现从仿真验证到嵌入式部署的全流程闭环。

该工具箱可实现一站式的控制系统设计，图形化配置更是大大加快了开发速度，也降低了设计的门槛。

详细内容可移步：MATLAB控制系统校正工具sisotool的使用

Matlab-自动化控制系统设计5控制系统的校正

（3） PLECS仿真软件简介

PLECS是由瑞士Plexim GmbH公司开发的系统级电力电子仿真软件，专为电路与控制系统的联合仿真设计，尤其适用于电力电子变换器、电机驱动及传动系统的建模与分析。

其核心优势在于 仿真速度与精度 ：采用理想开关模型（零导通电阻与无穷大开路电阻），避免了传统仿真中吸收电路带来的复杂性，并通过离散状态空间算法优化步长控制，显著提升仿真效率（比Simulink快2.5倍以上）。

PLECS提供 双版本支持 ——Blockset版（作为Simulink工具箱，实现电路与控制的协同仿真）和Standalone版（独立运行，集成控制与电路元件库），兼容Windows、Linux等多平台。

其功能覆盖 热仿真 （支持温度相关的损耗建模与热阻网络分析）、丰富的电力电子元件库（如无刷电机、三相变压器、齐纳二极管）以及自动C代码生成（嵌套版），可无缝衔接实时硬件部署。全球工业界（如西门子、ABB、松下）及学术界（清华大学、曼彻斯特大学）广泛采用其进行电力电子系统设计与教学，典型应用包括逆变器开发、电机控制及新能源变流器优化。

详细内容可移步：PLECS的基本介绍

3. 补偿器的设计流程

利用PLECS仿真软件的阻抗扫频（通过对电路扫频，得到bode图数据）
matlab的System Identification 系统辨识工具箱（将上面的bode数据拟合为传递函数）
matlab的sisotool控制系统设计工具（对系统进行补偿，自动设计控制环路的参数）
sisotool计算的的补偿器参数写入单片机中，进行闭环控制

本文以BUCK降压电路为例，演示使用工具进行自动环路设计过程。

设计目的输入电压60V，降压输出24V，电路仿真数据如下：

四、PLECS阻抗扫频与Bode图数据获取

打开仿真模型，点击Simulation下的analysis tools，选择AC sweep，如下：

进入AC sweep后，配置好选项，即可点击start analysis，如下：

经过软件的阻抗扫频以后，即可得到该BUCK电路的传递函数：

进入到如下界面：

波德图导出为：

从图中可以看出，这个电路的传递函数是一个二阶系统。

信号建模的传递函数计算可以参照我的另一篇博客： BUCK电路设计方法与PID补偿器参数整定方法

将伯德图数据以CSV格式导出，并保存。

导出的数据如下：

可以看到，频率的单位是HZ，在导入到matlab的系统辨识工具箱时，需要将其转化为rad/s的格式。

五、Matlab系统辨识工具箱传递函数拟合

1. 数据预处理

创建.m脚本文件，将导出的csv文件和脚本文件放在同一个文件夹中。

将数据导入到matlab的系统辨识工具箱时，需要对其进行预处理，以及将其导入到matlab的工作台，运行下面这段程序：

data = readmatrix('buck_i.csv');
freqHz = data(:,1);
ampDb = data(:,2);

amp = 10.^(ampDb/20);
pha = data(:,3);
freq = freqHz*2*pi;

运行程序后，在matlab的工作台可以看到以下数据：

· 其中，freq是频率，pha是相位，amp是幅值。

2. 导入数据到System Identification

先打开System Identification，如下：

开始导入数据，点击导入数据，点击Freq domain data，如下：

然后，就可以在操作台看到：

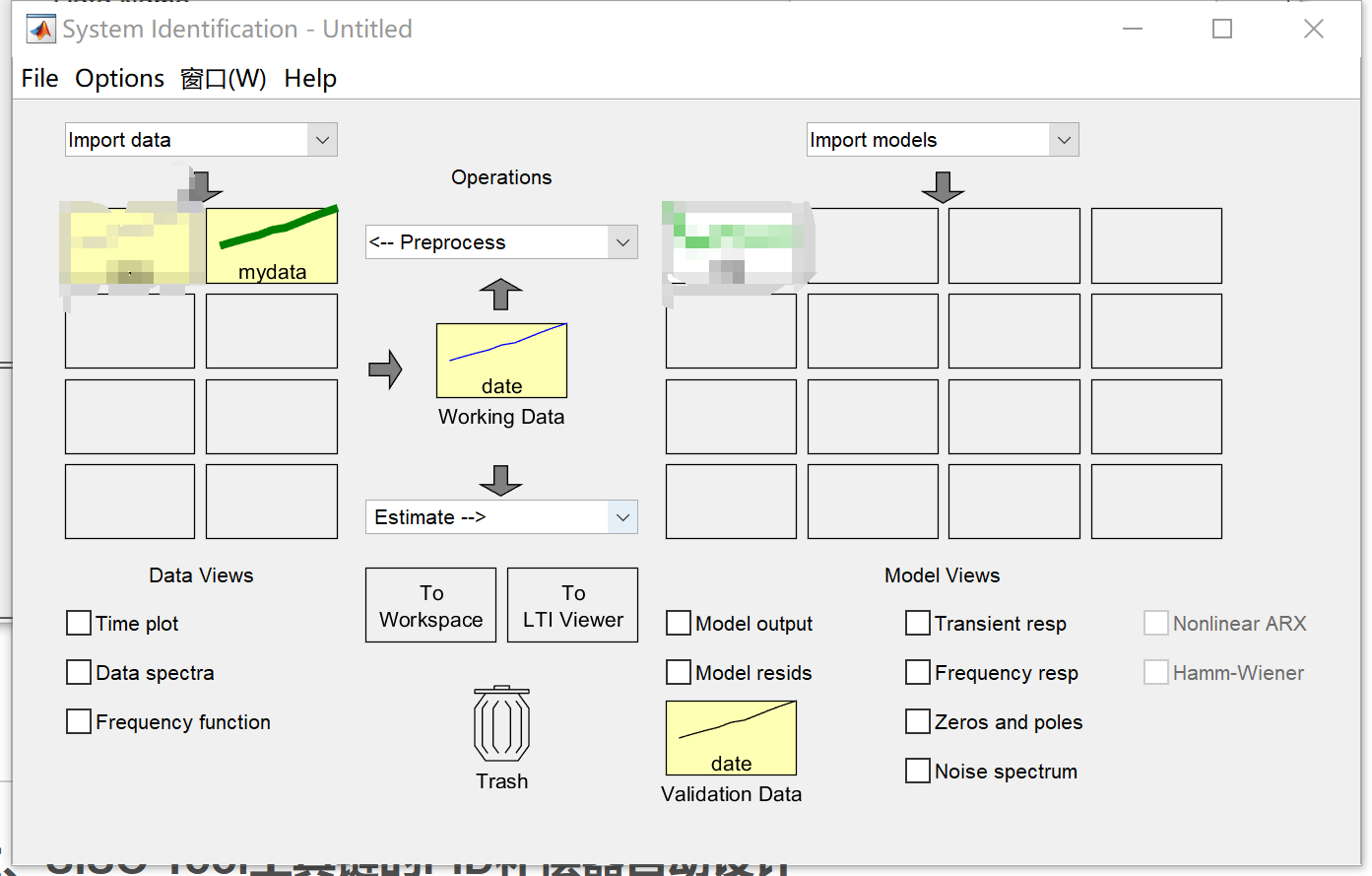
可以勾选下面的frequency resp 来看导入的伯德图，将其与plecs的伯德图进行对比：

注意频率单位。

接下来，选择估计传递函数：

选择两极点，单零点的数据进行拟合方式：

在操作台上会得到：

tf2就是拟合后的传递函数，可以勾选下面的frequency resp 来看他的伯德图。

双击下面的选项：

得到拟合后的传递函数：

拟合精度高达99.5%

将该传递函数复制下来，即可导入到sisotool工具，进行自动设计。

六、SISO Tool工具链的PID补偿器自动设计

运行下面这段程序，将传递函数数据导入到工作区：

fenzi = [9.541e04,3.598e08];
fenmu = [1,3767,2.879e07];
BUCK_I_G = tf(fenzi,fenmu)
bode(BUCK_I_G)

在命令行窗口输入 sisotool ，并运行，打开控制系统设计器，如下：

编辑架构，具体原理参照上一篇博客：

选择框架，导入传递函数：

选择补偿方式为PID补偿：

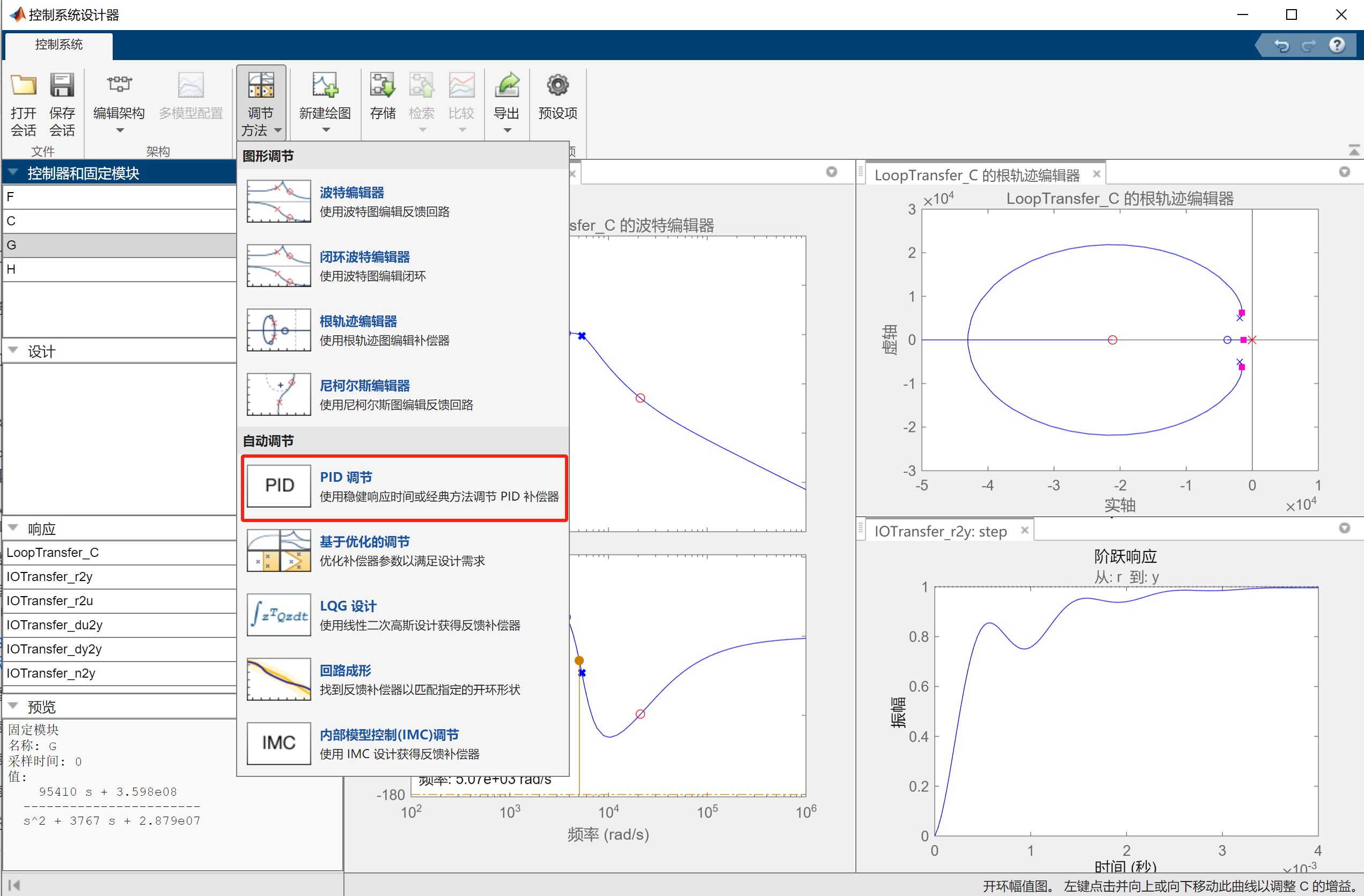
选择补偿后系统的的穿越频率和相位裕度：

可以看到系统补偿后 伯德图 ， 根轨迹图 ， 阶跃响应曲线，点击左边栏中的C，左下角出现补偿器的传递函数：

将得到的补偿器参数写入仿真，即可完成闭环设计。

七、双闭环仿真设计

1. 电流内环设计

将上面得到的电流内环参数写入到PLECS软件中，如下：

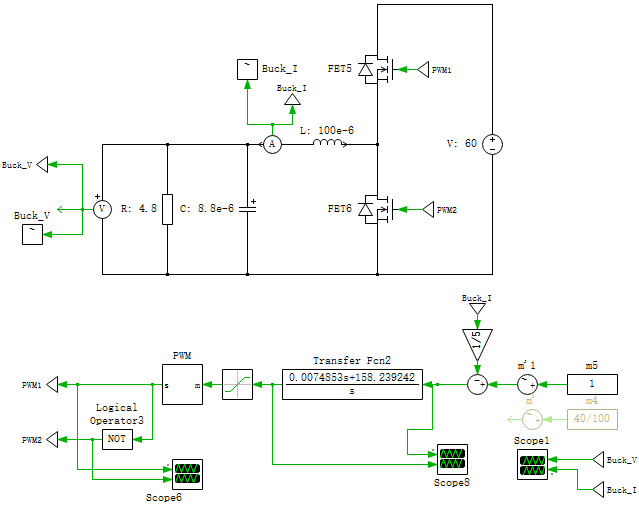
开始仿真，得到电流电压波形：

可见，仿真波形基本满足预期。

接下来，使用同样的办法，设计电压外环补偿器：

扫频得到电压外环的传递函数，如下：

2. 电压外环设计

3. 波形对比

八、参数离散化与硬件实验验证

1. 补偿器参数离散

下面给出matlab离散传递函数程序：

I_fenzi = [0.0074853,158.239242];
I_fenmu = [1,0];
I_G = tf(I_fenzi,I_fenmu)
bode(I_G)
hold on;
bc_z = c2d(I_G,1/50000,"tustin");
[num_z,num_m] = tfdata(bc_z,'v');
vpa(num_z,7)
vpa(num_m,7)
bode(tf(num_z,num_m,1/50000))

蓝色为连续域传递函数，红色为离散域传递函数，效果如下，可以看到相似度很高：

2. 实验平台介绍

正面：

背面：

3. 实验结果展示

正在调试中.................

九、总结与扩展方向

1. 技术优点

高效性与自动化
- 工具链闭环：PLECS仿真→系统辨识→SISO Tool参数整定，减少人工计算与试错成本，显著提升设计效率。
- 频域数据驱动：基于扫频的Bode图拟合传递函数，规避理论建模误差，提升模型可信度。
理论精度高
- 仿真环境理想化：无硬件噪声干扰，模型参数（电感/电容）严格符合理论值，便于验证控制算法核心逻辑。
- SISO Tool优化算法：可精确满足相位裕度、穿越频率等频域指标，仿真结果具备理论参考价值。
快速原型验证
- 参数可直接移植：从仿真到代码部署无缝衔接，缩短从设计到实验的周期。

2. 技术缺点

忽略实际硬件干扰
- ADC采样问题：未考虑采样噪声、混叠效应（超出奈奎斯特频率的高频信号混叠至低频），导致实际控制信号失真。
- 环路执行负载率：仿真假设控制器实时运行（无计算延迟），但单片机中断处理、任务调度可能引入额外滞后。
离散化与量化误差
- 连续域参数直接离散化（如Tustin变换）未适配实际采样率，可能引发相位损失或稳定性问题。
- ADC/DAC量化位数限制，导致控制量分辨率不足（如12位ADC引入的电压测量误差）。
非理想元件特性
- 仿真模型忽略寄生参数（电感DCR、电容ESR），导致实际频响与仿真Bode图偏差（如高频相位跌落）。

对比总结
维度	PLECS+Matlab自动设计	实际工程系统
模型精度	依赖理想化仿真模型	受硬件噪声、寄生参数、离散化影响
抗干扰能力	无环境干扰，理论纯净	需处理ADC混叠、PCB噪声、负载瞬变
实时性	假设零延迟闭环	受限于单片机算力、中断响应时间
参数鲁棒性	针对固定工况优化	需适配宽输入/负载范围及元件公差

3. 扩展方向

- - - 为克服仿真设计与实际系统的偏差，需从“理想模型驱动”转向“实测数据驱动”，核心改进方向如下：
  - 硬件在环验证替代纯仿真建模
    - 问题：PLECS仿真依赖理想元件模型，无法反映实际电路寄生参数（如电容ESR、电感DCR）及PCB布局噪声。
    - 解决方案：采用TI SFRA工具直接对硬件电路扫频，获取包含真实干扰与非线性特性的Bode图，彻底规避理论建模误差。
  - 离散化与抗混叠设计优化
    - 问题：PLECS+Matlab流程忽略ADC采样混叠效应与离散化相位损失，导致数字控制器性能下降。
    - 解决方案：基于TI Compensation Designer的离散化参数自动适配，结合抗混叠滤波器设计与Nyquist频率约束，确保数字控制环路稳定性。
  - 多工况鲁棒性优化
    - 问题：仿真仅针对固定工况设计，未覆盖实际宽负载/输入电压范围下的参数鲁棒性需求。
    - 解决方案：通过SFRA多条件扫频（如轻载/重载、输入瞬变），提取动态频响特征，利用Compensation Designer生成自适应补偿参数，提升系统抗扰动能力。