数字逻辑：布尔代数的运用之最大最小项

组合电路一般是怎么设计的呢？：

有的时候可以不用真值表，直接根据语句转换。但适用范围较小。

真值表很好画，那怎么转换成逻辑表达式呢？：

与或式： 

可以这样想：既然中间的主要链接式是或，1对或影响大，就关注1。接下来压力来到了与这一边，与的话3个都要是1，那么就要妙用非了。 

或与式：

 道理同上。

最后的来的式子可以化简，然后变成逻辑电路。

最大项，最小项（maxterm,minterm）

定义：可以看到，全部积起来就是最小项（因为这样一般更小）；全部合起来就是最大项。

元素可以是原变量，也可以是反变量。

最小，最大项的特点：

最小，最大项的编号就是“这是唯一可以使结果等于1\0的输入”。 

同时，这种唯一的输入也唯一的对应一种最小/大项，换了其他项就要变成0\1了。

一些性质：

最小项的反是最大项, 最大项的反是最小项：

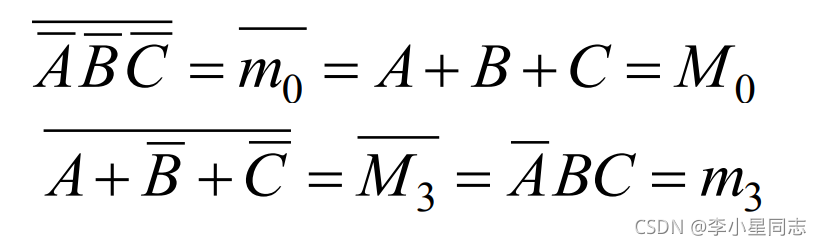
注意：反对应的项编号是与其相对应的。毕竟，“唯一输入使结果为1”反过来就是“唯一输入使结果为0”

全部最小项的和是1，全部最大项的积是0.

一部分最小项的和取反是其他的最小项的和

注意：不管ABC是什么，都只有一个最小项会是1，一个最大项是0.就是自己的编号。

标准与或式，或与式还记得吗？现在可以辨识为最小，最大项之和了。

 

最大项的：

以最小项为例，这个书写过程实际上是先找到1的项。刚刚说过，每个最小项只有一个可以使输出为1的输入，一种输入也只能使一个最小项为1，那么这个输入当然就会有一个最小项与其对应，之前的结果也是如此。输入可以看成2进制，刚刚也说过输入就是编号，于是就可以直接写出对应的最小项。最大项同理。

这样，用真值表可以快速地写出其对应的逻辑表达式了。

讲完了最小，最大项，还有一个无关项。

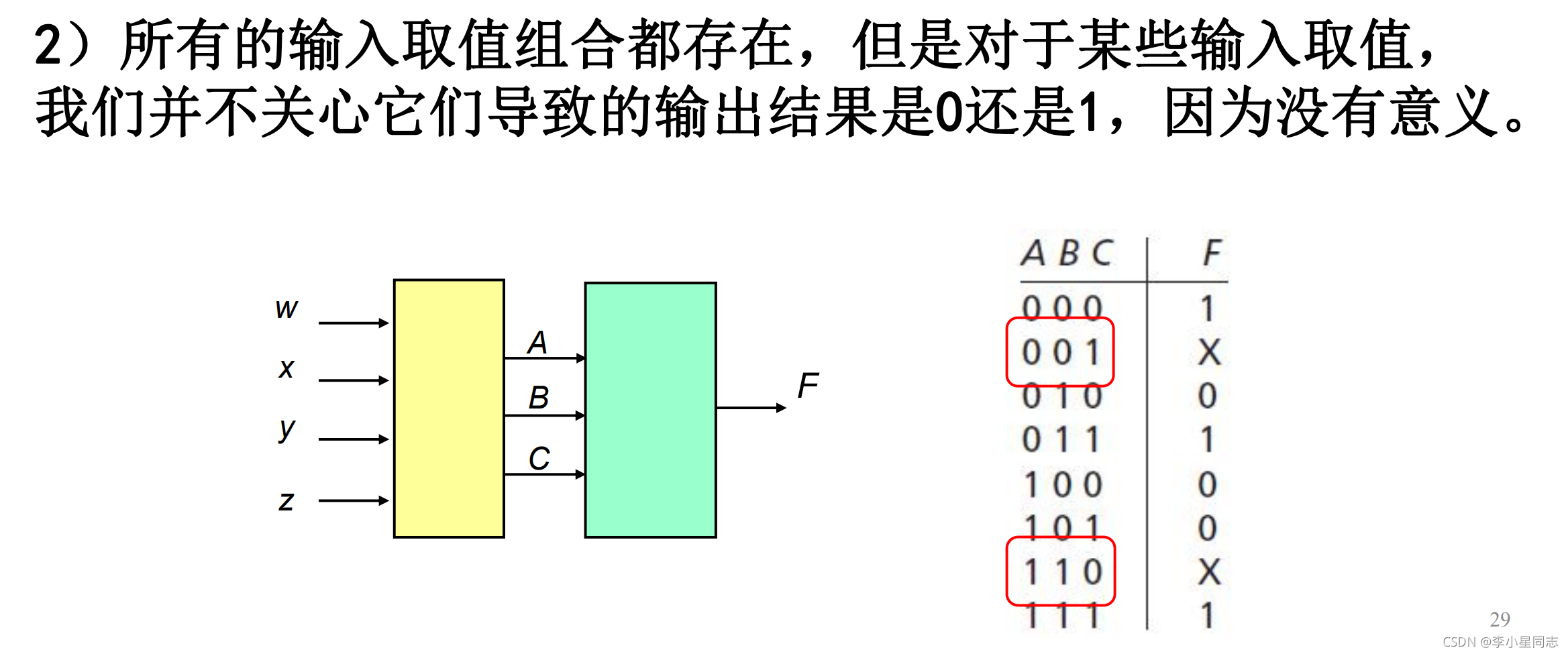
 最小项是m，最大项是M,无关项是d/D,和最小项在一起时是d,最大项在一起是D.