研究背景及意义
- 通常用样条表示一条曲线,其中拉格朗日多项式,贝塞尔样条,B-样条,三次埃尔米特样条以及非均匀有理B样条均广泛使用。
- 用控制点跳调整样条通常分为两大类:一类是样条曲线不经过控制点,而是接近控制点,这类问题称为拟合问题;一类是样条曲线严格经过控制点,这类问题称为插值问题。
- 拟合问题有着计算量小的优势,但它难以实现精准的控制;插值问题可以实现精准的控制,但通常需要解方程,因而计算量较大。
- 通常对样条插值曲线都有两个要求:一个是连续性,即样条在拼接点处的n阶导数一致,另一个是光顺性,曲线需要尽可能少的曲率极值点。
- 网格曲面的应用较为广泛,其中包括三角形网格,四边形网格和六边形网格。
- 在实际应用中,让网格每个面尽可能接近正多边形是网格优化的重要目标,提高网格质量是计算几何中的重要优化问题。
- 材料中的拉力不一定来自直接的拉力,还有一部分来自材料承受的剪应力。
- 将曲面设计成一种特殊的形状,使曲面内部的挤压力可以完全平衡去曲面自身的重力,这样就可以避免了弯矩和剪应力的产生,这种最稳定的形状称为“自支撑曲面”。
- 把曲面离散成网格过程称为有限元分析的前处理过程。三角网格和四边形网格是二维有限元分析前处理最常用的两种网格。
- 有限元分析通常期待四边形网格的每个面都接近正方形,且每个顶点都发出4条边。在高斯曲率非0的曲面上构造每个顶点都发出4条边的四边形剖分通常是做不到的,因而四边形网格必然有度不为4的顶点,称为奇异点。
- 如果一个曲面的四边形剖分得到的网格网格奇异点比较少,且从奇异点发出的边可以把去曲面分割成曲边矩形的形状,这种剖分生成的网格成为结构化网格。
- 自动生成结构化网格是计算几何学术领域中的前沿问题。
- 优化奇异点的位置让奇异点发挥抵消高斯曲率的作用,让每个面的内角都接近直角以保证更接近矩形。让每个面上的两组对边的长度尽可能接近以保证面的长宽比接近正方形。
研究现状
- 用适当的参数化方法构造二次有理贝塞尔样条,可以让他们达到C1连续,如果把拼接点处的两个样条的曲率约束为相同的,则可以达到G2连续。
- 圆锥曲线的拟合精度已被证明可以小于O(h4),而且能到达G2连续。
- 目前已有方法可以构造出极值点更少的圆锥曲线样条,这个方法的大致思路是分别找出样条拼接点和曲线上的曲率极值点并且去除掉,并调整切线的方向增强曲线的连续度。
- 曲率的导函数是描述样条光顺性的重要指标。从整体上来看,每条圆锥曲线至多有4个曲率极值点,一段圆锥曲线没有极值点的条件可以用一个可视化的几何模型表示。
- 目前对于圆锥曲线样条的研究都未能摆脱参数的制约。
- 人们通常用参数方程和隐式方程研究网格的性质,并发展一套微分几何理论,人们根据该理论导出:纯张力生成曲面,即极小曲面的平均曲率为0,有压强差的张力生成的曲面的平均曲率为常数,即欧拉-拉格朗日方程。
- 重心Voronoi图方法是最著名的三角形优化方法。Pinkall和Polthier使用了迪利克莱能量的极小化来生成极小曲面。当前大部分方法都是基于平均曲率流,让曲面沿着定义在三角网格上的离散的平均曲率流渐变。
- 边翻转算法是引入最早,也是最简单的网格优化方法,可以与平均曲率流的构造交替操作,从而生成曲面的同时提高网格的质量,让网格顶点分布更加均匀。在提高优化速度方面,稀疏线性求解器可以大大增加拉普拉斯算子的优化效果。
- 网格质量可以用顶点平均法和边翻转操作优化,但是这样会影响面积能量。因此,Surface Evolver实际上是对面积能量和优化能量的一个折中。Surface Evolver的网址具体如下所示:http://facstaff.susqu.edu/brakke/evolver/evolver.html
- 在顶点非常密集的情况下,重心Voronoi图的优化函数与网格面积的平方几乎等价,因而把优化函数与曲面体积的线性组合,可以构造平均曲率曲面。这种方法把网格质量和网格形状结合在了一起,使得常平均曲率的生成更加鲁棒。但是这种方法生成的极小曲面有着更大的曲率逼近误差,这是因为这种方法采用的能量函数与真实的面积能量函数并非严格等价。
- 可以使用拉格朗日变形曲面模型来实时模拟符合物理规律的水滴动画,这类算法主要关注流体的模拟,并不关注网格质量和表面形状的精度。
- 可以使用有限元分析来对偏微分方程的数值进行求解,然而有限元分析只能对已经确定的形状求力学方程的数值解,难以用来确定未知曲面的形状。
- 粒子-弹簧模型是一种求解弹性力学问题的方法,应用在几何构造中可以求解形变量很大的力学问题,因此可以用来设计自支撑曲面。但是,该模型可能会导致严重的形状扭曲。
- 把弹性力学中的拉普拉斯方程转化为离散形式,并基于离散曲率建立了自支撑曲面的力学方程,从而构造自支撑曲面。
- 自支撑曲面中的艾里应力函数可以用来实现参数化,并在上面构造B样条,从而增加曲面的平滑性。
- 目前的四边形构造方法中,除了谱分解方法,其余方法都是基于参数化的。参数化方法可以保证四边形网格的结构化程度。四边形网格的结构化程度可以通过重构来提升,最常用的方法是基于对奇异点发出的网格线的追踪。
- 共形映射成为构造结构化四边形网格的重要理论。根据黎曼映射定理,任何单连通区域都可以与单位圆盘建立共形映射,这从理论上保证了在单连通区域建立共形映射的可行性。共形映射的建立通常基于求解拉普拉斯方程,共形映射的一个局限性是它只能在单连通区域上建立。
- 四边形网格与三角形网格有个非常关键的不同点,就是每个面上的所有点的共面未必能保证。在玻璃窗的设计中,要求四边形网格四点严格共面,这称为PQ网格。
- 使用人工标记的方法和主曲率方向估计方法可以使四边网格线的方向沿着曲面的主曲率线。基于主曲率线的方向引导,正交流场可以通过构造一个含有整数变量和实数变量的平滑能量函数,并对它极小化自动生成。决定平滑能量函数中的整数值却是一个NP-Hard问题。目前求最好近似解的方法是混合整数求解方法。
- 基于复数的特正向量的方法对奇异点的分布有了一定的改进效果。减少奇异点的数量有助于提高四边形网格的结构化程度。合并异号的奇异点是最常见的减少奇异点的方法。
- 由于流场的奇异点无法完全消除,因此全局的参数化必然会有分割线。但是如果参数在分割线两边满足一定的关系,可以在采样生成的网格避免分割线。
- 正交流场的两个方向是严格垂直的,但是如果局部的参数畸变过大,会导致网格形状的走样甚至缺陷。
创新点
- 圆锥曲线插值问题抛弃了传统的基于参数化的方法,提出了新的几何概念,即弦切比,并把它作为一个自变量应用于约束函数和优化函数的构造。
- 根据顶点在切平面上移动对曲面形状影响很小,在法向量上移动对网格质量影响很小的特点,把两个有冲突的目标函数的梯度投影在了不同的空间中,避免了他们的相互影响,从而保证生成离散曲面的网格质量和精度。
- 利用变分原理建立了三维自支撑曲面和四维旋转极小超曲面之间的联系,导出了自支撑曲面构造的优化方程,分析了它于张力生成曲面的联系,并把张力生成曲面的构造方法应用于自支撑曲面的构造。
- 提出了一种有效的圆锥曲线插值方法:找出了基于弦切比端点曲率和曲率变化率的表达式,并应用于构造连续函数。对施密特正交化方法做了改进。
- 提出了一种构造高质量的离散张力生成曲面的方法:研究了面积函数沿着法向量的凸性质,提出了拟合面积的近似函数。利用了面积加权顶点法向估计的性质,保证了迭代优化过程的稳定性质。
- 建立了基于四维空间极小旋转曲面构造自支撑曲面的相关理论:利用自支撑曲面平衡方程于四维空间旋转极小曲面方程的相近性导出了他们的等价性。提出了基于平均曲率的估计离散自支撑曲面的构造方法。
- 建立了二维流形上的N旋转对称场的奇异点的局部优化理论:利用高斯-波涅公式导出了N旋转对称场与静电场的相似性。利用麦克斯韦张量导出了奇异点调整方向的计算方法。
- 提出了一种减少角度畸变的曲面参数化方法:提出了每条边上的方法系数的概念。设计了求解约束最小二乘 问题的投影共轭梯度法。
豪斯道夫距离
http://www.cnblogs.com/yhlx125/p/5478147.html
-
豪斯多夫距离量度度量空间中真子集之间的距离。Hausdorff距离是另一种可以应用在边缘匹配算法的距离,它能够解决SED方法不能解决遮挡的问题。
-
设X和Y是度量空间M的两个真子集。那么豪斯多夫距离dH(X,Y)是最小的数r使得X的闭r—领域包含Y,Y的闭r—邻域也包含X。
-
在欧几里得几何中常与一个类似概念,称为等距同构下的豪斯多夫距离。设X 和Y是欧几里得空间中两个紧的图形,则DH(X,Y)是dH(I(X),Y)取所有欧几里得空间的保距变换I的最小值。这距离量度X和Y离等距差多少。
-
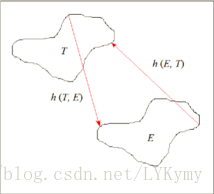
h (T, E) 表示了模板边缘点与最近图像边缘点之间的最大距离;h (E, T) 的定义与h (T, E) 互为对称,它表示了图像边缘点与最近模板边缘点之间的最大距离。Hausdorff距离是由这两个距离的最大值决定。
-
-
相关参考网址:https://blog.csdn.net/eloudy/article/details/70837560
狄利克雷函数
-
狄利克雷函数是一个定义在实数范围上、值域不连续的函数。狄利克雷函数的图像以Y轴为对称轴,是一个偶函数,它处处不连续,处处极限不存在,不可黎曼积分。这是一个处处不连续的可测函数。
-
-
-
狄利克雷条件
- 狄利克雷条件是一个信号存在傅里叶变换的充分不必要条件。
- 狄利克雷边界条件,常微分方程的“第一类边界条件”,指定微分方程的解在边界处的值。
- 狄利克雷条件括三方面:
(1 )在一周期内,连续或只有有限个第一类间断点;
(2)在一周期内,极大值和极小值的数目应是有限个;
(3)在一周期内,信号是绝对可积的。
间断点
-
间断点是指:在非连续函数y=f(x)中某点处xo处有中断现象,那么,xo就称为函数的不连续点。间断点可以分为无穷间断点和非无穷间断点,在非无穷间断点中,还分可去间断点和跳跃间断点。如果极限存在就是可去间断点,不存在就是跳跃间断点。
-
有限元分析
-
有限元分析(FEA,Finite Element Analysis)利用数学近似的方法对真实物理系统(几何和载荷工况)进行模拟。利用简单而又相互作用的元素(即单元),就可以用有限数量的未知量去逼近无限未知量的真实系统。
-
有限元分析是用较简单的问题代替复杂问题后再求解。它将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。
-
有限元是那些集合在一起能够表示实际连续域的离散单元。
-
拉普拉斯方程
-
拉普拉斯方程(Laplace's equation)又称调和方程、位势方程,是一种偏微分方程。
-
拉普拉斯方程表示液面曲率与液体表面压强之间的关系的公式。
-
二阶偏微分方程的拉普拉斯方程为
-
两个自变量的拉普拉斯方程具有以下形式:
拉普拉斯算子
- 拉普拉斯算子(Laplace Operator)是n维欧几里得中的一个二阶微分算子,定义为梯度(▽f)的散度(▽·f)。拉普拉斯算子也可以推广为定义在黎曼流形上的椭圆型算子,称为拉普拉斯-贝尔特拉米算子。拉普拉斯算子定义为
- 满足▽·▽f=0 的函数f, 称为调和函数。
艾里应力函数
-
应力函数(stress function)亦称艾里应力函数.微分方程的一种解.是定义在弹性体所占区域上的函数.
-
-
应力常用公式:https://wenku.baidu.com/view/8a9d7deebceb19e8b8f6bab6.html
B样条曲线
-
B-样条是贝兹曲线(又称贝塞尔)的一种一般化,可以进一步推广为非均匀有理B样条(NURBS),使得我们能给更多一般的几何体建造精确的模型。
-
B样条曲线曲面具有几何不变性、凸包性、保凸性、变差减小性、局部支撑性等许多优良性质。
-
B样条曲线方程可表示为
-
-
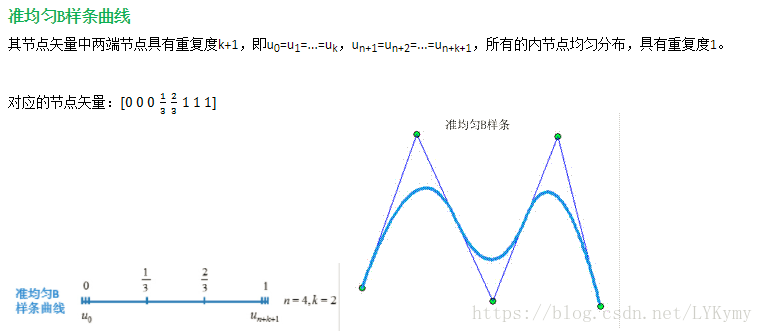
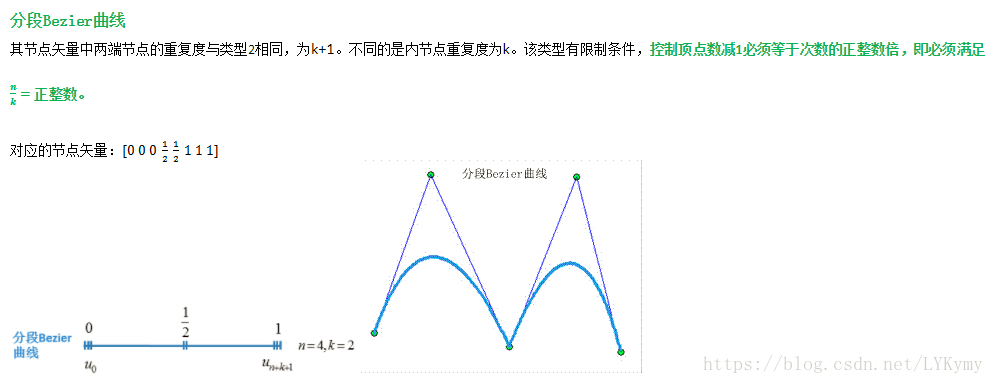
根据节点矢量中节点的分布情况不同,可以划分4中类型的B样条曲线。不同类型的B样条曲线区别主要在于节点矢量,对于具有n+1个控制顶点
的 k次B样条曲线,无论是哪种类型都具有n+k+2个节点
。
-
-
-
-
-
-
谱分解方法
-
特征分解(Eigendecomposition),又称谱分解(Spectral decomposition)是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。
-
-
-
参考网址:http://www.360doc.com/content/17/0813/12/25664332_678846612.shtml
NP-Hard问题
- NP-hard,其中,NP是指非确定性多项式(non-deterministic polynomial,缩写NP)。所谓的非确定性是指,可用一定数量的运算去解决多项式时间内可解决的问题。















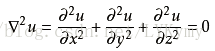
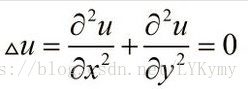
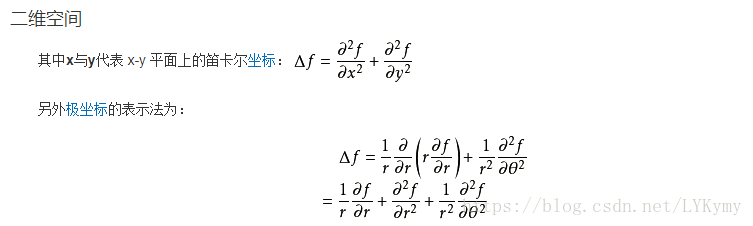


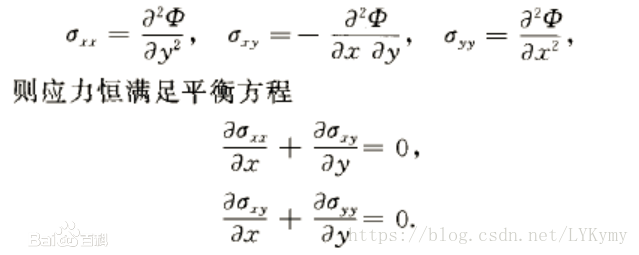

![clip_image010[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233217441-1151218157.gif)



















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








