stochastic pool

看到很多的对CNN的改造的文章中都是对pool做东西，最近看到一个随机池化，就好奇的去看了一下

可以参看这篇文章 Stochastic Pooling for Regularization of Deep Convolutional Neural Networks

在caffe中是支持最大池化，均值池化，随机池化的

在使用中常见的是mean-pooling和max-pooling，下面就简单介绍一下stochastic pooling

　　stochastic pooling方法非常简单，只需对feature map中的元素按照其概率值大小随机选择，即元素值大的被选中的概率也大。而不像max-pooling那样，永远只取那个最大值元素。

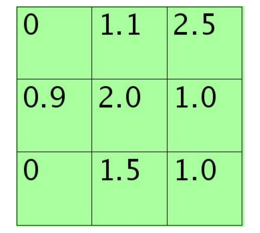
　　假设feature map中的pooling区域元素值如下：

 　　

　　3*3大小的，元素值和sum=0+1.1+2.5+0.9+2.0+1.0+0+1.5+1.0=10

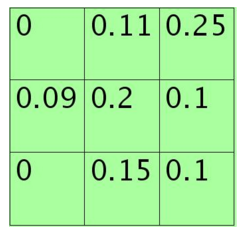
　　方格中的元素同时除以sum后得到的矩阵元素为：

 　　

　　每个元素值表示对应位置处值的概率，现在只需要按照该概率来随机选一个，方法是：将其看作是9个变量的多项式分布，然后对该多项式分布采样即可，theano中有直接的multinomial()来函数完成。当然也可以自己用01均匀分布来采样，将单位长度1按照那9个概率值分成9个区间（概率越大，覆盖的区域越长，每个区间对应一个位置），然随机生成一个数后看它落在哪个区间。

　　比如如果随机采样后的矩阵为：

 　　

　　则这时候的poolng值为1.5

　　使用stochastic pooling时(即test过程)，其推理过程也很简单，对矩阵区域求加权平均即可。比如对上面的例子求值过程为为：

 　   0*0+1.1*0.11+2.5*0.25+0.9*0.09+2.0*0.2+1.0*0.1+0*0+1.5*0.15+1.0*0.1=1.625 说明此时对小矩形pooling后的结果为1.625.

　　在反向传播求导时，只需保留前向传播已经记录被选中节点的位置的值，其它值都为0,这和max-pooling的反向传播非常类似。

      下面是原文中给出的一个整体的计算的图

   在计算时的时候train计算主要是进行随机采样的方式进行计算，在test时主要是使用概率进行计算的选取哪一个，是均值池化和最大池化的一个中间

   区域吧。

　　Stochastic pooling优点：

　　方法简单;

　　泛化能力更强;

　　可用于卷积层（文章中是与Dropout和DropConnect对比的，说是Dropout和DropConnect不太适合于卷积层. 不过个人感觉这没什么可比性，因为它们在网络中所处理的结构不同）。