深入浅出讲解LDA主题模型（一）

最近总是遇到主题模型LDA（Latent Dirichlet Allocation），网上的博客写的天花乱坠而不知所以然，无奈看了最厚的《LDA数学八卦》，观完略通一二，记录于此~顺便放两张遇到的图，挺有意思的，共勉吧：

主题模型

首先我们来看什么叫主题模型~我们来考虑一个问题：判断文本相关程度。怎么判断呢？是看相同词语出现的次数来判断吗（TF-IDF）？显然这太草率了。从内容角度来讲，只要两篇文章的主题是相同的，这两篇文章就是相关的。比如一片文章介绍的是京东618，另一片是天猫双11，主题基本相同。
我们来看看生成一篇文章有怎么的手段：

Unigram Model

假设我们的词典一共有V个词$v_1,v_2,...,v_V$,那么最简单的主题模型就是认为上帝（你！就！是！上！帝！┗|｀O′|┛ ）是按照如下的游戏规则产生文本的：

※※※※※※※※※
Unigram Model
※※※※※※※※※
1.上帝只有一个骰（tou，有文化真可怕）子，这个骰子有V个面，每个面对应一个词，各个面的概率不一；
2。每抛一次骰子，抛出的面就对应的产生一个词；如果一片文档中有n个词，上帝就是独立的抛n次骰子产生这n个词。

PLSA

这个就是一个主题模型啦~Hoffman认为上帝是按照如下规则生成文本：

※※※※※※※※※※
PLSA Topic Model
※※※※※※※※※※
1. 上帝有两种类型的骰子，一类是doc-topic骰子，每个doc-topic骰子有K个面，每个面都是一个topic的编号；一类是topic-word骰子，每个topic-word骰子有V个面，每个面对应一个词；

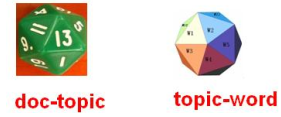
2. 上帝一共有K个topic-word骰子，每个有一个编号，编号1到K
3. 生成每篇文档之前，上帝都先为这篇文章制造一个特定的doc-topic骰子，然后重复如下的文档词语生成过程:

• 投掷这个doc-topic骰子，得到一个topic编号z
• 选择编号为z的topic-word骰子，投掷这个骰子得到一个词

---

贝叶斯学派

如果没有贝叶斯学派，大家都是频率主义学派，我们的这篇博文到此就差不多该结束了。我们看看贝叶斯学派有什么高见，作了什么补充吧。先简要的看看两个学派有什么区别：

频率主义学派

万物皆可频。每个事件都有个确定的概率，我们可以通过做实验得到频率，再用这个频率去估计概率。比如，扔硬币，正面向上一定是有个概率的。我们扔了5000次，有2000次正面向上，3000次背面向上，这这个概率就是2/3（频率主义内心OS：我不听我不听，我都做了5000次试验了，你还想怎样(；′⌒`)）。

贝